1. Случайные события (классическое и статистическое определение вероятности события).

Событие называется случайным, если в результате опыта оно может произойти или не произойти.

В классической схеме вероятность любого события определяется как отношение числа m благоприятных для события A элементарных исходов к общему числу элементарных исходов n.

П ри статистическом определении в качестве вероятности события принимают его относительную частоту. Ф-ла, где m - число испытаний, в которых событие A наступило, n - общее число произведённых испытаний.

2. Теорема сложения вероятностей несовместных событий.

Объединением (суммой) двух событий А и В называется событие D , происходящее тогда и только тогда, когда наступает хотя бы одно из событий А или В.

В ероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

3 . Условная вероятность. Теорема умножения вероятностей.

Условная вероятность — вероятность одного события (А) при условии, что другое событие (В) уже произошло.

Пересечением (произведением) двух событий C и D называется событие F, происходящее тогда и только тогда, когда наступают одновременно оба события C и D.

P(CD)=P(C)xP(D/C) – совместные события

P(CD)=P(C)xP(D) – несовместные события

4. Теорема сложения вероятностей совместных событий.

Объединением (суммой) двух событий А и В называется событие D , происходящее тогда и только тогда, когда наступает хотя бы одно из событий А или В.

Вероятность суммы совместных событий вычисляется по формуле.

.

5. Формула полной вероятности.

Если событие А может произойти только при выполнении одного из событий  , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

.

Эта формула называется формулой полной вероятности.

6. Формула Баесса.

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H1, H2, ..., Hn, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).

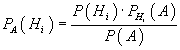
7. Повторные независимые испытания (формула Бернули).

Пусть проводятся независимые испытания (такие, при которых вероятность появления события в каждом испытании не зависит от результатов предыдущих испытаний). Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

В формуле Бернулли используется число сочетаний.

Повторюсь, что для реализации схемы Бернулли необходимы два условия:

1) независимость проводимых испытаний;

2) p = const (постоянное значение вероятности появления события)

8. Формула Пуассона.

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например,   вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:

 – среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для   и  . При больших   рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).