4. Расчет трехфазных электрических цепей переменного тока

1. При соединении звездой U_Л поэтому

Так как есть нейтральный провод, то

2. Вычисляем сопротивление фаз и углы φ определяем по диаграм­мам сопротивлений.

3. Определяем фазные токи:

Дано: U_л=220 В; R_А=50 Ом;

R_B=72 Ом; R_CA=2,5 Ом;

X_{L B}=32 Ом; X_{L C}=90 Ом;

X_{C A}=72 Ом.

Определить: Z_A, Z_B, Z_C, I_A, I_B, I_C,

P, Q, S.

ВГПК 390202. К13. 021 ПЗ

21

4. Чтобы вычислить ток в нейтральном проводе, нужно построить векторную диаграмму цепи. На векторной диаграмме под углом 120 друг относительно друга строятся векторы фазных напряжений одинаковой длины. Векторы фазных токов строятся в масштабе под вычисленными уг­лами φ по отношению к фазным напряжениям.

Выбираем масштаб:

Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов:

5. Определяем активные мощности фаз:

6. Активная мощность трехфазной цепи:

Р = Р_А + Р_В+ Р_C = 104,3+186,7 +0 Вт.

6. Определяем реактивные мощности фаз:

Q_A = U_A ∙ I_A ∙ sinφ_A = 127 ∙ 1,44 ∙ sin(–55,2 ) = -150,1 BAр,

Q_B = U_B ∙ I_B ∙ sinφ_B = 127 ∙ 1,61 ∙ sin24 = 83,1 BAр,

Q_C = U_C ∙ I_C ∙ sinφ_C = 127 ∙1,41 ∙ sin90 =179 BAр.

7. Реактивная мощность трехфазной цепи:

8. Вычисляем полную мощность каждой фазы и всей цели:

S_A = U_A ∙ I_A = 127 ∙ 1,44 = 182,8 B∙A;

S_B = U_B ∙ I_B = 127 ∙ 1,61 = 204,4 B∙A;

S_C = U_C ∙ I_C = 127 ∙ 1,41 = 179 B∙A;

ВГПК 390202. К09. 021 ПЗ

22

ВГПК 390202. К09. 021 Э3

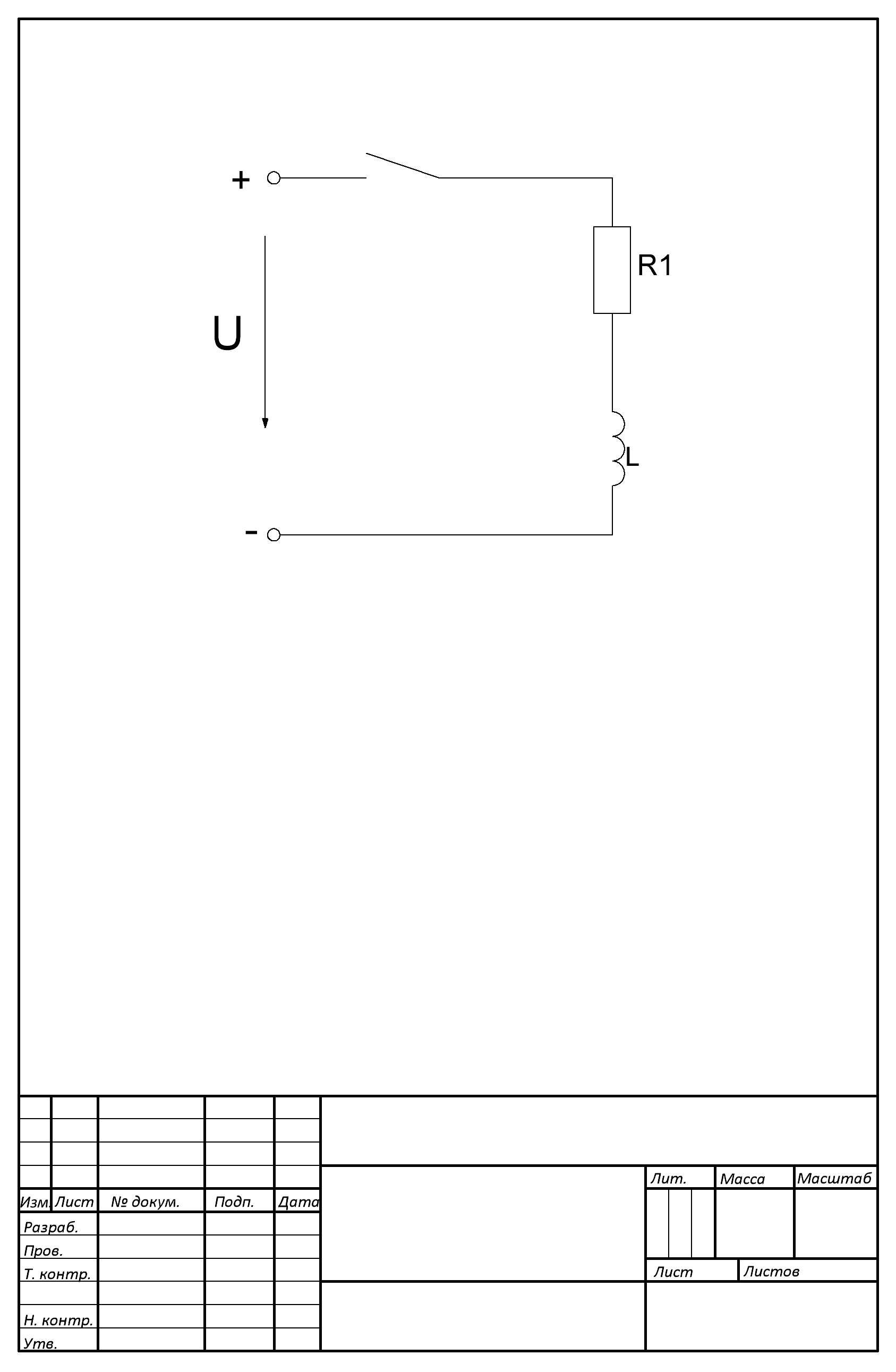
Переходные процессы в электрических цепях

Схема электрическая принципиальная

Группа ВР-33

Савельев

23

5. Переходные процессы в электрических цепях

До замыкания переключателя в положение ток в цепи равен нулю. (t = 0), ток в цепи будет таким же, как и в последний момент до начала коммутации, т. е. i₀ = 0.

После коммутации ток стремится достигнуть величины установив­шегося тока (i_ycт), но на основании первого закона коммутации изменяется не скачком, а постепенно.

Согласно схеме

U 70

i_ycт = I = ---- = ---- = 1 А,

R 70

Чтобы найти закон изменения переходного тока, запишем уравнение в общем виде

i = i_ycт + i_св = i_ycт + A

В этой формуле

i_{св =} A

где i_св - свободная составляющая тока;

А - постоянная интегрирования;

е = 2.71 - основание натурального логарифма;

τ - постоянная времени переходного процесса,

L

τ = --- , где R - величина сопротивления,

R через которое проходит переходный ток;

t - текущее время.

Определяем постоянную интегрирования, полагая t = 0, тогда уравнение

i = i_ycт + i_cв = i_ycт + A примет вид: i₀ = i_ycт + А, т. к. е⁰ = 1

значит, А = i₀ – i_ycт = 0 – I, то есть А = – I.

Дано:

L=0,8 Гн;

R=70 Ом;

U=70 В.

ВГПК 390202. К13. 021 ПЗ

24

Находим постоянную времени переходного процесса

L 0,8

τ = --- = ------------ = 0,011 c.

R 70

Практическая длительность переходного процесса t = 5 τ = 5 ∙ 0,01 = 0,05 с

Строим график переходного тока i = f(t),

задавшись моментом вре­мени t = 0, t = τ, t = 2 τ, t = 3 τ, t = 4 τ, t = 5 τ.

Значения переходного тока для заданных значений времени:

t = 0, i₀ = 1 ∙ (1 – ) = 1 ∙ (1 – 1) = 0 A;

t = τ, i₁ = 1 ∙ (1 – ) = 1 ∙ (1 – e^-1) = 0,62 A;

t = 2τ, i₂ = 1 ∙ (1 – ) = 1 ∙ (1 – е^-2) = 0,86 А;

t = 3τ, i₃ = 1 ∙ (1 – ) = 1 ∙ (1 – е^-3) = 0,94 А;

t = 4τ, i₄ = 1 ∙ (1 – ) = 1 ∙ (1 – е^-4) = 0,98 А;

t = 5τ, i₅ = 1 ∙ (1 – ) = 1 ∙ (1 – е^-5) = 0,99 А.

Закон изменения ЭДС самоиндукции можно получить из формулы

e_L = – L = – L (I – I ) = – I ∙ L = – I ∙ L ∙ = – I ∙ R ∙ = – U

-i В нашем случае e_L = – 70 В

Значения е для заданных значений времени следующие:

t = 0, e₀ = – 70∙e⁰ = – 70B

t = τ, е₁ = – 70∙е^-1 = – 70 ∙ 0.367 = – 25,9 В;

t = 2τ, е₂ = – 70∙е^-2 = – 70 ∙ 0.135 = – 9,6 В;

t = 3τ, е₃ = – 70∙е^-3 = – 70 ∙ 0.049 = – 3,5 В;

t = 4τ, е₄ = – 70∙е^-4 = – 70 ∙ 0.018 = – 1,3 В;

t = 5τ, е₅ = – 70∙е^-5 = – 70 ∙ 0.007 = – 0,48 В.

Энергию магнитного поля при t = 2τ можно вычислить так:

L ∙ i₂² 0,8 ∙ 0,86²

W_M = -------- = ------------- = 0,3 Дж

2 2

ВГПК390202. К13. 021 ПЗ

25