1.2.2 Поиск кратчайшего пути

1.2.2.1 Метод обхода

Алгоритм Дейкстры является предпочтительным методом поиска кратчайших путей в графах со взвешенными ребрами и/или вершинами. Основная идея данного алгоритма очень похожа на основную идею алгоритма Прима. В каждом цикле мы добавляем одну вершину к дереву вершин, для которых мы знаем кратчайший путь из вершины . Так же, как и в алгоритме Прима, мы сохраняем информацию о наилучшем пути на данное время для всех вершин вне дерева и вставляем их в дерево в порядке возрастания веса.

Разница между алгоритмом Дейкстры и алгоритмом Прима состоит в том, как они оценивают привлекательность каждой вершины вне дерева. В задаче поиска минимального остовного дерева нас интересовал только вес следующего возможного ребра дерева. А при поиске кратчайшего пути нам нужна также информация о ближайшей к вершине вне дерева, т.е., кроме веса нового ребра, мы хотим знать еще и расстояние от вершины к смежной с ней вершине дерева.

Алгоритм находит кратчайший путь от заданной начальной вершины ко всем другим вершинам графа, включая требуемую конечную вершину .

Допустим, что кратчайший путь от вершины к вершине t графа G проходит через определенную промежуточную вершину . Очевидно, что этот путь должен содержать кратчайший путь от вершины к вершине x, в качестве префикса, ибо в противном случае можно было бы сократить путь 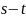, используя более короткий префиксный путь 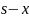. Таким образом, прежде чем найти кратчайший путь от начальной вершины к промежуточной вершине .

Алгоритм Дейкстры работает поэтапно, находя на каждом этапе кратчайший путь от вершины к некой новой вершине. Говоря конкретно, вершина такова, что сумма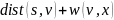 минимальна для всех необработанных 1≤ i≤ n, где – длина ребер между вершинами i и j, a – длина кратчайшего пути между ними.

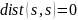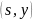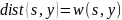Здесь напрашивает стратегия, аналогичная динамическому программированию. Кратчайший путь от вершины к самой себе является тривиальным, при условии отсутствия ребер с отрицательным весом, поэтому . Если является самым легким ребром, входящим в вершину , то это означает, что . Определив кратчайший путь к вершине , мы проверяем все исходящие из нее ребра, чтобы узнать, не существует ли лучшего пути из начальной вершины к какой-либо неизвестной вершине через вершину .

1.2.2.2 Алгоритм обхода

Ниже представлен псевдокод алгоритма поиска кратчайшего пути.

Таблица 1.2 – Псевдокод алгоритма Дейкстры.

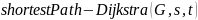
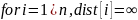
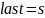
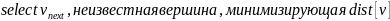
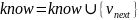
1.2.2.3 Анализ обхода

Временная сложность алгоритма Дейкстры, в том виде, как он реализован здесь, равна .

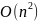Длина кратчайшего пути от начальной вершины start к созданной вершине t равна точно значению distance[t]. Каким образом мы можем найти сам путь с помощью алгоритма Дейкстры? Мы следуем обратным указателям на родительские узлы от вершины t, пока мы не дойдем до начальной вершины (или пока не получим -1, если такого пути не существует).

Алгоритм работает правильно только на графах, в которых нет ребер с отрицательным весом. Дело в том, что при построении пути может встретиться ребро с отрицательным весом настолько большим по модулю, что оно полностью изменит оптимальный путь от вершины s к какой-то другой вершине, которая уже включена в дерево.[1]