Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО»

Кафедра теоретических основ компьютерной безопасности и криптографии

Обход в ширину. Алгоритм Дейкстры.

КУРСОВАЯ РАБОТА

студентки 1 курса 131 группы

специальности 090301.65 Компьютерная безопасность

факультета компьютерных наук и информационных технологий

Шакировой Виолетты Александровны

Научный руководитель (руководитель)

аспирант _____________ Гавриков А. В.

Зав. кафедрой профессор, к.ф -м.н. _____________ Салий В. Н.

Саратов 2013

СОДЕРЖАНИЕ

Введение 3

1 Теоретическая часть 4

1.1 Общие теоретические основы 4

1.2 Алгоритмы обхода графа 4

1.2.1 Обход в ширину 4

1.2.1.1 Метод обхода 4

1.2.1.2 Алгоритм обхода 5

1.2.1.3 Анализ обхода 6

1.2.1.4 Корректность 6

1.2.2 Поиск кратчайшего пути 7

1.2.2.1 Метод обхода 7

1.2.2.2 Алгоритм обхода 9

1.2.2.3 Анализ обхода 9

1.2.2.4 Корректность 10

2 Практическая часть 13

2.1 Реализация обхода в ширину 12

2.2 Реализация алгоритма Дейкстры 14

Заключение 16

Список использованных источников 17

ВВЕДЕНИЕ

Поиск кратчайшего пути – вопрос, который востребован сегодня повсеместно. Нахождение кратчайшего пути используется практически везде, начиная от поиска оптимального маршрута между двумя объектами на местности, в системах автопилота, нахождение оптимального маршрута при перевозках, коммутации информационного пакета в Internet и т.д. Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Существует множество алгоритмов поиска кратчайших маршрутов. Три наиболее эффективных из них:

1) алгоритм Дейкстры (используется для нахождения оптимального маршрута между двумя вершинами);

2)алгоритм Флойда (для нахождения оптимального маршрута между всеми парами вершин);

3)алгоритм Йена (для нахождения k-оптимальных маршрутов между двумя вершинами)

В данной курсовой работе будет подробно рассмотрен базисный алгоритм - обход в ширину, и сам поиск кратчайшего пути между двумя вершинами во взвешенном графе – алгоритм Дейкстры. В первой части работы я предоставлю теоретические знания, которые дадут некоторые начальные сведения о графах. В последующих главах будет представлен метод обхода, алгоритм на псевдоязыке и сама реализация в виде программного кода.

1 Теоретическая часть

1.1 Общие теоретические основы

Введем соответствующую терминологию.

Граф – это упорядоченная пара множеств 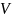– это подмножество вершин (или узлов), а – упорядоченное или не упорядоченное множество ребер, соединяющих пары вершин из .

Взвешенный граф – граф 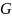, где каждому ребру или вершине присваивается числовое значение, или вес.

Не взвешенный граф – граф , где разные вершины или ребра не различаются по весу.

Ациклический граф – граф, не имеющий циклов.[1]

Временная сложность алгоритма – это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. Во многих задачах размер выхода не превосходит или пропорционален размеру вход – в этом случае можно рассматривать временную сложность как функцию размера только входных данных.[2]

Список смежности – эффективный способ представления разреженных графов. Это структура, где для каждой вершины хранится в динамическом списке смежные ей вершины.

Разреженный граф – граф, в котором в действительности ребра определены только для малой части возможных пар вершин.[1].