16. Числовые ряды.
Пусть имеется 
последовательность чисел 
.
Опр.: Выражение
наз. числовым рядом. 
- члены числового ряда. 
- общий член числового ряда.
Опр.: Последовательность
;
;
;...;
последовательность
частичных сумм ряда или отрезки. Частичные
суммы образуют
последовательность, поскольку число
членов
.
Опр.: ряд (1) наз. сходящимся, если сходится последовательность его частичных сумм.
сумма
ряда (1). ряд (1) наз. расходящимся, если
предел (
)
бесконечен или не существует.
Т.1: (необходимое
условие сходимости)
если ряд 
сходится, то его общий член стремится
к 0 при
.
.
Док-во: Пусть
ряд сходится, это означает, что 
представим 
ч.т.д.
замеч.: стремление к 0 общего члена не является достаточным условием сходимости.
Критерий Больцано-Коши о сходимости числового ряда.
Т.2:
для того чтобы ряд с общим членом
сходился необх. и дост., чтобы вып. след.
условие: (
)
(2)
(1)
док-во: I. Необходимость. Пусть (1) сходится, след. сходящийся ряд его последовательных сумм
(
)
.
Пусть m=n+p
для определенности рассмотрим разность
.
=
выполняется
условие (2).
Достаточность. Пусть для ряда (1) вып. усл. (2). Представим сумму под знаком модуля в виде разности
;
n+p=m.
Для (
)
вып. усл. (
)
(
)
– сх. 
(1) сх. ч.т.д.
Основные свойства сходящихся рядов.
Пусть дан ряд (1)
Опр.:
ряд, полученный из данного ряда, путем
отбрасывания конечного числа первых
членов, наз. остатком ряда.
(2) n-ый
остаток ряда.
Т.1: Если ряд сходится, то сходится и любой из его остатков.
Обр.: Если сх. к-л остаток ряда, то сх. и сам ряд.
док-во:
пусть ряд сх. Обозначим через
m-ую
частичную сумму n-ого
его остатка.
сумма
n-ого
ост. ряда.
Пусть
нек. остаток ряда (1)
p=m+n.
. Зафиксируем
n,
.
ч.т.д.
Действия над числовыми рядами.
Т.:
Если члены сх. ряда умножить на один и
тот же множитель 
,
то его сх. не нарушится, а сумма умножится
на
.
(3)
док-во:
рассмотрим 
, 
.
ч.т.д.
Т.:
Два сх. ряда
(4) и 
(5) можно почленно складывать, при этом
сумма полученного ряда 
где
A
– сумма (4) ряда, B
– сумма (5) ряда, C
– сумма 
(6).
док-во: обозначим
через 
- n-ую
частичную сумму ряда (6)
.
.
ч.т.д.
умножение ряда.
пусть даны
и 
,
рассмотрим ряд 
Т.(Коши):
Если ряд 
сх.
и 
сх., то сходится ряд
и сумма ряда равна произведению сумм
данных рядов.
док-во:
рассмотрим
S
– ую частичную сумму 
.
,
где 
сходится.
ч.т.д.
Достаточные признаки сх. полохительных рядов.
Т.:
пусть даны два положительных ряда
и
.
Если для 
вып. нер-во 
то
из сходимости
вытекает сходимость
,
а из расходимости первого ряда вытекает
расходимость второго ряда.
док-во:
,
тогда (
)
возр. и огр. сверху 
сх.
расх. 
сх. 
сх., а это противоречит тому, что
расх. ч.т.д.
Т.(признак
Коши):
Пусть
положительный, если (
)
сх.,
а если (
)
расх.
док-во: пусть
(
)
тогда 
а ряд 
сх., т.к. 
сх.
пусть (
)
не
выполняется необх. условие сх., значит
расх. ч.т.д.
Т.(признак Даламбера):
пусть
положит.,
тогда если (
)
,
то
сх.
(
)
расх.
док-во:
(
)
,
0<q<1
…
сх.
сх.
(
)
возр.
необх.усл. не вып.
расх. ч.т.д.
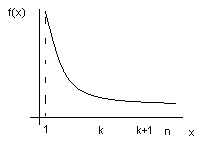
Т.(интегр.
признак Коши): Пусть
положит.,
если сущ. полож., монотонно убыв., непр.
ф-ия 
при 
и 
то данный ряд сх. 
когда сх. 
.
док-во:
сх.
сх.
,
т.к. 
огр. сверху
(
)
сх., ряд
сх.
Пусть
сх.
сх.
(
)
– огранич. (
).
, 
огр. сверху
сх. ч.т.д.
Знакочередующиеяс ряды. Теорема Лейбница.
Опр.: Ряд, кот-ый сод. как положит., так и отриц. члены наз. знакопеременными.
Опр.: Ряд, у кот. любые 2 соседних числа имеют разные знаки, наз. знакочередующимся.
Т.(Лейбница):
Пусть ряд 
знакочередующийся ряд и 
lkz
тогда данный ряд сходится.
док-во:
рассмотрим последовательность (
)
возр.
,
(
)
огр. сверху
(
)
сх. 
=
т.к. 
сх. ч.т.д.
Абсолютно сходящиеся ряды. Условно сходящиеся ряды.
рассм. ряд
(1), к-ый сод.
число как положит., так и отриц. членов
(2).
Т.: если сх. ряд из модулей членов данного ряда, то сх. и сам ряд (1).
док-во:
пусть ряд (2) сх., по критерию Больцано-Коши
(
)
сх. ч.т.д.
Опр.: Сх. ряд наз. абсолютно сх., если сх. и ряд из модулей его членов.
Опр.: Сх. ряд наз. условно сх., если ряд из модулей его членов расх.
Т.(Дирихле): если ряд абсолютно сх., то ряд полученный из него любой перестановкой членов также сх. и суммы этих рядов равны.
док-во: I.
положит. сх., 
его сумма
ряд, получ. из ряда
путем перестановки его членов.
,
что 1) ряд сх. 2) 
…
, 
,
из 
,
,
произв. абс. сх. ряд
положит.
ряд. сумма этих рядов = S
сх. по I
ч. и сумма его 
,
перестановка в ряде 
приведет к перестановке в ряде 
и 
,
а сумма не меняется, тогда 
ч.т.д.
Т.(римана): если усл. сх. ряд, то каково бы ни было число В конеч. или бесконеч., можно так переставить члены ряда, чтобы ряд имел суммой число В.
док-во:
I.
Пусть В конеч. число, 
k-ый
положит. член ряда, 
m-ый
член отриц. по модулю.
ряда
расх., можно взять столько членов, чтобы
сумма была больше любого наперед
заданного конеч. числа.
продолжим процесс до бесконечности,
получим ряд
;
;
II.
B=
.
Выбирая посл-ть чисел 
и беря столько пол. чисел, чтобы было
.
получаем подобный ряд, имеющий сумму
+
ч.т.д.
Понятие нормы. Ряды в нормированных пространствах.
Опр.:
Пусть 
вект. пр-во над 
.
ф-ия 
,
всюду опр. на 
,
наз. нормой, если:
(E,
)
– нормированное пространство.
Опр.: Ряд
в (E,
)
– это формальное выражение вида 
(1)
ряд (1) наз. сх-ся,
если сх-ся посл-ть (
),
где 
;
суммой ряда (1)
наз-ся элемент 
.
Опр.:
ряд (1) наз-ся абсолютно сх-ся, если сх-ся
числовой ряд 
(2)
Пр-ие: Если ряд сх-ся абсолютно, то он сходится (в банаховом пр-ве – полное нормированное пространство)
если ряд (1) сх-ся,
то (
)
фундаментальна, т. е. (
)
или 