Сведение криволинейного интеграла первого рода к определенному.

Криволинейные интегралы первого рода вычисляют сведением его к определенному интегралу.

1. Пусть задана уравнением: , тогда .

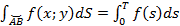2. Пусть кривая задана параметрически 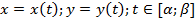, тогда .

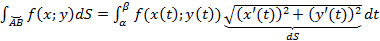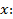
3. Пусть параметром будет , тогда .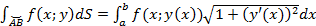

Замечание: Аналогично для функции можно построить криволинейный интеграл первого рода по пространственной кривой .

Сведение криволинейного интеграла второго рода к определенному.

1. Пусть кривая задана параметрически , тогда

2. В частности пусть параметром будет т.е. 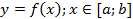, тогда 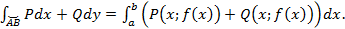Аналогично если параметр .

Формула Грина.

Т еорема: Пусть в некоторой области непрерывно дифференцируемы 2-е функции и и пусть внутри этой области расположен простой замкнутый контур . Обозначим через область , ограниченную этим контуром, тогда справедлива формула: .

Док-во:

1. .

2. .

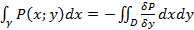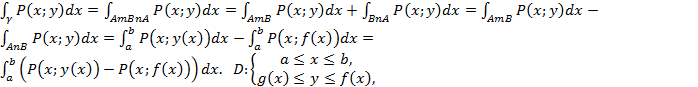
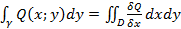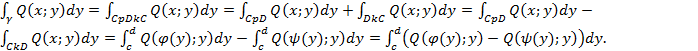
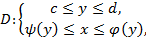
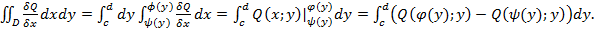
Итог: Сложением равенств доказываемых в 1 и 2получаем необходимое выражение.

Условия независимости криволинейного интеграла второго рода от пути интегрирования.

Теорема: Следующие 4 условия Эквивалентны между собой:

1. Выражение 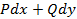является полным дифференциалом некоторой функции .

2. 

3. 

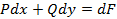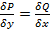
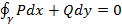
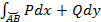4. не зависит от выбора пути интегрирования, а зависит лишь от начальной и конечной точек.

Док-во: правые части равны по теореме о равенстве смешанных производных.

следует из формулы Грина .

; ; .

15.1 Квадрируемая фигура и ее площадь

Обозначим символом площадь многоугольной фигуры . Напомним, что площадь многоугольной фигуры-это неотрицательное число, удовлетворяющее след. Св-вам.

1. Инвариантность. Если 2 многоугольные фигуры и 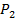равны между собой, то .

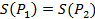2. Аддитивность. Если и -две многоугольные фигуры без общих внутренних точек и символ 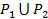обозначает объединение этих фигур, то .

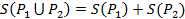3. Существование единицы. Площадь квадрата со стороной, равной единице измерения длины, равна единице измерения площади.

Величина площади фигуры существенным образом зависит от выбора единицы измерения в рассматриваемой системе координат.

Введем понятие площади для произвольной плоской фигуры . Рассмотрим для этого всевозможные многоугольные фигуры , целиком содержащиеся в , и многоугольные фигуры , целиком содержащие .Фигуры будем называть вписанными в , а фигуры -описанными около . Числовое множество площадей всех вписанных многоугольных фигур ограничено сверху, например, площадью любой описанной многоугольной фигуры . Поэтому это множество имеет конечную точную верхнюю грань

Которую будем называть нижней площадью фигуры .Если в фигуру нельзя вписать ни одного многоугольника, то по определению полагается . Аналогично,числовое множество площадей всех описанных около фигуры многоугольных фигур ограничено снизу, например, площадью любой вписанной многоугольной фигуры или нулем, и поэтому у него существует конечная точная нижняя грань

Называемая верхней площадью фигуры . Очевидно,что .

Плоская фигура называется квадрируемой (т.е. имеющей конечную площадь), если . Число называется при этом площадью фигуры (по Жорадну). Будем говорить, что плоская фигура имеет площадь, равную нулю, если эта фигура содержится в многоугольной фигуре сколь угодно малой площади.

Теорема(Необходимое и достаточное условие квадрируемости). Для того, что плоская фигура была квадрируемой, необходимо и достаточно, чтобы ее граница имела площадь нуль.