14. Криволинейные интегралы первого рода

Пусть функция задана непрерывно в некоторой области и пусть в этой области кривая задана параметрическими уравнениями .

Такая кривая будет называться гладкой если функции непрерывно дифференцируемы и на .

1) разобьем линию между точками и на бесконечно малые отрезки точками ;

2) внутри каждого отрезка выбираем точки  тем самым строим отмеченное разбиение ;

3) вычислим значение функции в этих точках  ;

4) обозначим через – длину и построим интегральную сумму: . Обозначим через максимальную из длин дуг .

Определение: если предел полученной интегральной суммы, не зависящий от отмеченного разбиения, то этот предел называется криволинейным интегралом 1-го рода и обозначается: .

Свойства криволинейного интеграла первого рода

1. Криволинейный интеграл линейной комбинации функций равен линейной комбинации интегралов этих функций . Это свойство означает, что криволинейный интеграл обладает свойством линейности по подынтегральной функции.

2. Если линию интегрирования разбить на части, то интеграл по линии равен сумме интегралов по её частям . Это свойство означает, что криволинейный интеграл обладает свойством аддитивности по линии интегрирования.

3. Криволинейный интеграл первого рода не зависит от направления интегрирования .

4. Если всюду на кривой функция , то .

5. Если всюду на кривой , то .(монотонность)

6. Если и – соответственно наименьшее и наибольшее значения функции на кривой , то

Криволинейный интеграл 2-го рода.

Задача: Найти работу совершенную мат. точкой при движении её по дуге в плоском силовом поле.

Определение: Плоским силовым полем называется векторная функция двух переменных (т.е. зависит от координат точки)

Д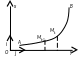 ано: . Решение: разобьем на части. В качестве отмеченных точек выберем правые концы частей. Для каждой частичной дуги выберем .

; и это проекции силы на оси координат. ;

– интегральная сумма.

Обозначим . Если , то он называется работой.

Определение: Пусть в некоторой области заданы две функции и и пусть в этой области задана гладкая кривая .

1) разобьем линию между точками и на бесконечно малые отрезки точками ;

2) в качестве отмеченных точек выберем правые концы дуг;

3) вычислим значения функций и в этих точках;

4) обозначим через и проекции частичной дуги на и построим интегральную сумму: . Обозначим . И вычислим предел от интегральной суммы.

Если данный предел существует и не зависит от отмеченного разбиения, то он называется криволинейным интегралом 2-го рода и обозначается: .

Замечание: Если кривая есть отрезок || одной из координатных осей, то криволинейные интегралы 1-го и 2-го рода совпадают.

Криволинейным интегралом по координате x по кривой AB от функции называется предел (если он существует) интегральной суммы при : .

Криволинейным интегралом по координате y по кривой AB от функции называется предел (если он существует) интегральной суммы при : .

Свойства криволинейного интеграла первого рода

1. .(ориентированность)

2. если, функции и интегрируемы на кривой по переменной , то функция также интегрируема на дуге по переменной и справедливо равенство . Аналогично по переменной (линейность);

3. Если дугу разбить на части, то интеграл по дуге равен сумме интегралов по её частям . Это свойство означает, что криволинейный интеграл обладает свойством аддитивности по линии интегрирования. Криволинейный интеграл 2-го рода можно считать и по замкнутому контуру. Для таких интегралов существует специальное обозначение (аддитивность).

4. Интеграл по замкнутому контуру не зависит от пути интегрирования.

5. Если замкнутый контур ограничивающий область разбит на 2-е части, то интеграл по замкнутому контуру, ограничивающему область равен сумме интегралов по контурам ограничивающих области .