23. Аксиоматическое определение вероятности. Вероятностное пространство. Условные вероятности. Формула полной вероятности, формула Байеса.

Пространство элементарных событий - совокупность всех мысленных исходов испытаний.

Пример:

1. Подбрасываем монету 1 раз

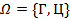
2. Монета бросается до тех пор, пока не выпадет герб

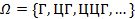
Исходы испытания - элементарные события ω

Событием будем называть любое подмножество пространства

достоверное событие, невозможное событие.

Невозможное событие - событие, которое в данном испытании не наступает

Достоверное событие Ω- событие, которое обязательно произойдет в испытании.

Суммой событий А и В назыв. событие А+В, состоящие в наступлении хотя бы одного из событий А или В.

Произведением событий А и В назыв. событие А*В, состоящие в одновременном наступлении событий А и В.

Пример: Бросаем 1, 2, 3, 4, 5, 6}

А – «четное число очков», А={2, 4, 6}

В – «число очков больше 4», В={5, 6}

А+В={2, 4, 5, 6}, АВ={6}.

Если наступление означает, что наступает событие А, то говорят, что элементарное событие благоприятствует А.

Если наступление А означает, что наступит В, то говорят, что А влечет В.

Разностью событий А и В назыв. событие , которому благоприятствуют те ЭС А, которые не благоприятствуют В.

Пример:

противоположное событию А.

События А и В называют несовместными, если они не могут наступить одновременно

Замечание: т.е. не совместные события

Пусть дана система событий F для (ПЭС).

Система событий F называется алгеброй событий, если

1. 

2. 

3. 

Алгебра F называется алгеброй событий, если

Числовая функция Р определенная на алгебре событий F называется вероятностью (вероятной мерой) события А, если выполняются следующие аксиомы:

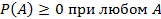1. (неотрицательность)

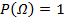2. (нормированность)

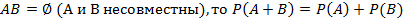3. (аддитивность)

4. Для убывающей цепочки событий 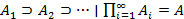выполняется условие 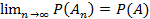(непрерывность)

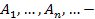5. несовместные события, то 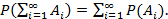(счетная аддитивность).

Свойства вероятности:

1. 

Док-во: В силу несовместности по аксиоме 3

2. 

Док-во: т.к. , то по аксиоме 3

⇒ по аксиоме 1

3. 

Док-во:

⇒ по аксиоме 3

Тройка называется вероятностным пространством.

Классическое определение вероятности:

Пусть конечно ( исходов), исходы испытаний несовместны и равновозможны (равновероятны)

Тогда число исходов, благоприятствующих А, число всех исходов испытания. Это и есть классическое определение вероятности (Лаплас)

Геометрическое определение вероятности:

Пусть имеется измеримая область , в которую случайно бросается точка. Имеется область А – «случайная точка, брошенная в область попадет в ».

Вероятность попадания в область не зависит от распределения , а пропорциональна мере .

, mes – мера.

Теорема: сложение несовместных событий (док-во ММИ)

Теорема: сложение совместных событий:

Условной вероятностью события А при условии, что событие В уже наступило назыв. число равное:

Свойства:

1. 

2. 

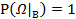
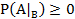
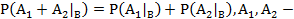3. несовместны.

Теорема умножения:

События А и В назыв. независимыми, если

События А и В независимы

Формула полной вероятности.

Гипотезы удовлетворяют условиям:

• 

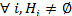
• (попарно несовместны)

• 

обра­зуют полную группу событий.

Совместно с гипотезами происходит событие А. Р(А) -?

формула полной вероятности.

Если А уже наступило,

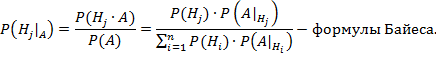
Формула Бернулли.

Одно и тоже испытание повторяют раз, при неизменных условиях (т.е. происходит независимых повторных испытаний). Каждое испытание имеет два исхода: «успех» - появление события А в данном испытании, «неудача» - не появление А.

Вероятность «успеха» в каждом испытании постоянна и равна , вероятность «неудачи»

А – событие «успех» наступит раз при независимых испытаниях.

Обозначим

Событию А благоприятствуют «цепочки» .

формула Бернулли.