21. Понятие функции комплексной переменной дифференцируемой в точке.
Определение:
Пусть задана 
.
Если 
поставлен в соответствии один или
несколько элементов из множества 
по некоторому закону то говорят, что
задана функция комплексного переменного
однозначная или многозначная соответственно
и обозначается 
.
Определение: Функция называется дифференцируемой в точке, если она имеет производную в этой точке.
Определение:
Производной функции f(z)
в точке
называется предел отношения приращения
функции к вызвавшему его приращению
аргумента при стремлении последнего к
0. 
Определение:
Функция называется дифференцируемой
в точке, если ее приращение 
б.м.
при 
.
(аналогично можно записать 
)
Дифференцируемость
функции комплексного переменного нельзя
получить из дифференцируемости её
действительной и мнимой части. Поэтому
дифференцируемость только действительной
и мнимой части ФКП, т.е. функций 
и 
принято называть 
,
а дифференцируемость, указанная в
определениях 
.
Замечание: С помощью последнего определения можно вывести все операции над производными для ФКП.
Теорема: (необходимое условие дифференцируемости функции): Если функция дифференцируема, то она непрерывна.
Док-во:
найдем предел: 
Беск. малому приращению аргумента
соответствует беск. малое приращение
функции
функция непрерывна. Док-но.
Теорема: Если функция дифференцируема, то дифференцируемы её действительная и мнимая части. (Обратное не верно)
Пусть функция 
частные производные функций u
и v
в
окр. точки (x,y),
непрерывные в точке (x,y).
Т2:( условия
Коши-Римана, критерий дифференцируемости
функции): Для того чтобы функция
комплексного переменного f(z)=
была дифференцируема в некоторой точке
чтобы
функции 
были
дифференцируемы как функции 2-х
действительных переменных и выполнялись
условия: 
.
При этом производная вычисляется по
одной из следующих формул:
;
Условия из теоремы называются условиями
Коши-Римана.
Док-во:
Необх:
Если 
дифференцируема доказать что 
- дифференцируемы и частные производные
связаны условием Коши-Римана.
б.м. при 
.
2 компл.числа равны, если равны их действительные и мнимые части.
и 
- дифференцируемы как функции 2
действительных переменных, т.к. 
- Беск. малые при 
(следует
из
).
.
Подставив данное выражение
и
получаем условия Коши-Римана: 
Дост:
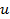и 
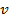- дифференцируемы, выполняются условия
Коши-Римана, доказать что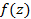 
дифференцируема. Т.е. ее приращение
.
и
– дифференцируемы; введем обозначения
– дифференцируема, т.е. 
;
– б.м. при 
.
– дифференцируема, т.е. 
;
– б.м.
при
.
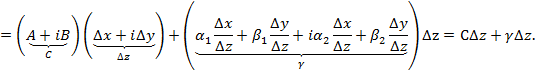
т.к.
,
аналогично 
.
их модули
тоже бесконечно малые при 
б.м. при
.
при
.
Свойство б.м.:
б.м. 
б.м. при 
б.м. при 
дифференцируема Т.к. 
,
а по усл. 
.
Аналитические функции.
Определение: Функция называется аналитической (голоморфной) в точке, если она дифференцируема в некоторой окрестности этой точки.
Определение: Функция называется аналитической (голоморфной) в области, если она дифференцируема в области.
Определение:
Функция
двух
действительных переменных называется
гармонической, если она удовлетворяет
уравнению Лапласа 
Теорема: Действительные и мнимые части аналитической функции являются гармоническими функциями.
Док-во:
т.к.
– аналитическая следовательно
дифференцируема следовательно, она
удовлетворяет условиям Коши-Римана
.
Продифференцируем первое по
,
второе по
:
.
Сложим полученные
равенства: 
Ф-я 
удовлетворяет уравнению Лапласа
- гармоническая.
Продифференцировав первый по , второй по и вычтя из первого, получим что - гармоническая.
Замечание:
Обратное не
верно т.к. если взять 2 гармонические
функции 
и
и связать их условием 
,
то поучится функция в большинстве
случаев не являющаяся аналитической
т.к., для дифференцируемости, а значит
и аналитичности этой функции требуется,
чтобы
и
были связаны условиями Коши-Римана.
Определение: Функция называется сопряжено гармонической к функции , если эти функции удовлетворяют условиям Коши-Римана.
Теорема: Если
сопряжено гармоническая к
,
то 
аналитическая.
Теорема: Всякую аналитическую функцию, с точностью до произвольной постоянной, можно восстановить по её действительной или мнимой части.
Замечание: Для того, чтобы восстановить аналитическую функцию задаются начальные условия.
Разложение аналитической функции в степенной ряд в окрестности данной точки.
Определение:
Выражение
вида 
заданное на множестве 
называется функциональным рядом.
Множество 
- сходится как числовой
называется областью сходимости
функционального ряда. 
.
Определение:
Функциональный
ряд вида 
называется степенным рядом, 
.Для
аналитической функции: 
.
Теорема: (Тейлора):
Функция
,
аналитическая в окрестности точки
может быть представлена в окрестности
этой точки степенным рядом 
,
причем этот ряд определен однозначно.
Определение: Функция называется аналитической в точке если она разложима в степенной ряд.
Определение: Функция называется аналитической в области, если в этой области она разложима в степенной ряд.
Если степенной
ряд сходится не только в точке
и не во всей комплексной плоскости, то
называемое радиусом сходимости степенного
ряда удовлетворяющее неравенствам: 
– ряд сходится; 
–
ряд сходится.
– круг сходимости.
Теорема: Степенной ряд можно почленно дифференцировать, причем круги сходимости данного и полученного рядов совпадают.
Теорема: Если в комплексной области функция разлагается в степенной ряд, то она дифференцируема (а значит и аналитична в круге сходимости) и более того такая функция бесконечно дифференцируема.
Справедлива и обратная теорема: если функция дифференцируема, то её можно разложить в степенной ряд.
Геометрический смысл модуля и аргумента производной.
аналитична в области
;
.
Дана кривая 
проходит через точку
.
Образом этой кривой на плоскости 
будет 
.
- Величина постоянная для данной точки
т.е. не зависит от выбора кривой.
Аргумент производной к данной функции в данной точке есть угол поворота данной функции при данном отображении.
Модуль производной есть коэффициент растяжения отображения (функции) в окрестности данной точки (есть отношение касательного вектора образа к длине касательного вектора данной кривой).
Конформное отображение.
Теорема: Свойство сохранения углов.
Если функция
дифференцируема, причем 
,
то угол между 2-мя кривыми, проходящими
через точку
равен углу между их образами при данном
отображении.
Определение: Отображение, которое сохраняет величины углов и имеет постоянный коэффициент растяжения, называется конформным.
Определение: Если отображение не меняет величины углов, но меняет их направление, то отображение называется анти конформным.
Теорема: Если
функция
дифференцируема в точке
b
,
то отображение
в этой точке является конформным.
Определение: Отображение называется конформным в области, если оно конформно в каждой точке этой области.
Линейная функция осуществляет конформное преобразование всей комплексной плоскости на себя.
Дробно-линейная функция осуществляет конформное отображение своей области определения в комплексную плоскость.
Степенная функция осуществляет конформное отображение всей комплексной плоскости в комплексную плоскость.