13. Двойные и тройные интегралы.

Определение 1. Цилиндрическим телом (см. рис. 1) называется тело, ограниченное:

· поверхностью, заданной уравнением z = f(x, y);

· плоскостью хоу;

· цилиндрической поверхностью с образующими, параллельными оси oz и направляющей l (замкнутой кривой в плоскости хоу).

Определение 2. Область D (см. рис. 2) называется правильной, если любая прямая, параллельная какой-либо из координатных осей, пересечёт границу области не более чем в двух точках.

О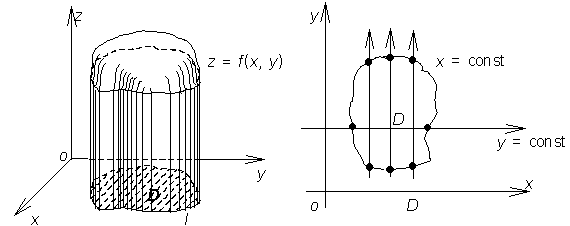 пределение 3. Диаметром области называется расстояние между наиболее удалёнными точками этой области.

Задача 1. Вычислить объём цилиндрического тела (см. определение 1), ограниченного поверхностью z = f(x, y) и плоскостью z = 0, когда область D является проекцией тела на плоскость хоу.

Решение. Пусть для определенности f(x, y) > 0 для всех точек (х, у) области D. Разобьём область D произвольным образом на n частей  (см. рис. 3), площади которых обозначим  . В каждой из частичных областей произвольно выберем точку   и вычислим в ней значение функции z_i = f(P_i), где i = 1, 2, …, n.

П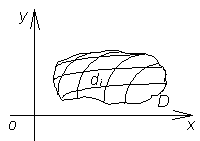 остроим на каждой частичной области d_i цилиндр с высотой h_i = f(P_i). Каждый из них ограничен сверху плоскостью z = h_i, где i = 1, 2, …, n, а объём его v_i подсчитаем по известной формуле (высоту умножаем на площадь основания)   Тогда приближённо весь объём будет равен сумме объёмов этих “элементарных” цилиндров:

Очевидно, таких сумм можно составить сколько угодно и величина их будет зависеть как от метода разбиения области D на части, так и от выбора точек Pi на каждой из этих частей.

За точный объём цилиндрического тела будем считать предел суммы (1), при неограниченном увеличении числа делений области на части, когда  , где   - наибольший из диаметров частичных областей d_i: .

Задача 2 (о вычислении массы плоской пластины). Пусть в некоторой замкнутой области D плоскости хоу задана непрерывная функция  - плотность распределения массы. Необходимо определить массу неоднородной пластины (толщиной пренебрегаем).

Решение. Разобьём область D произвольным образом на п частей   (рис. 3), площадь каждой из которых обозначим  . В каждой из частичных областей произвольно выберем точку   и вычислим в ней значение функции  . Предположим, что плотность каждого малого участка есть величина постоянная, равная , т. е. значение функции в точке P_i распространяем на весь участок d_i. Таким образом, каждую частичную область предполагаем однородной, масса её вычисляется по известной формуле , где i = 1, 2, …, n.

Просуммировав эти произведения по всей области D, мы получим приближённое значение искомой массы .

За истинную массу примем предел суммы (2), если он существует, когда число делений области D на части неограниченно растёт при одновременном уменьшении, т.е.  , где  - наибольший из диаметров частичных областей d_i: .

Теперь обобщим результаты решений обеих задач и дадим определение двойного интеграла. Пусть в правильной замкнутой области D плоскости хоу задана ограниченная функция z = f(x, y). Разобьём произвольным образом область D на п частичных областей d_i, в каждой из которых произвольно выберем точку . Пусть площадь частичной области равняется , где i = 1,2, …, n. Образуем суммы .

Выражение (3) - интегральная сумма Римана.

Определение 4. Предел сумм   при , если он существует и не зависит от способа разбиения области D на части   и выбора в каждой из них точек  , при условии,  что , где  - наибольший из диаметров частичных областей, называется двойным интегралом Римана от функции f(x, y) по области D и обозначается ; (4).

Другими словами, двойной интеграл есть такое число I, что для любого как угодно малого  найдётся  такое, что как только , так |I - Q_n| <  . Если такое число I существует, то функцию f(x, y) называют интегрируемой в области D.

Теперь подведём итог решения задач 1 и 2:

1) предел интегральной суммы (1) равен двойному интегралу .

Формула (5) служит для вычисления объёма цилиндрического тела, ограниченного плоскостью хоу и поверхностью z = f(x, y), и выражает геометрический смысл двойного интеграла;

2) предел интегральной суммы (2) равен двойному интегралу

Формула (6) служит для вычисления массы неоднородной плоской пластины с переменной плотностью  и выражает физический смысл двойного интеграла.

З адача 3 (О нахождении массы тела переменной плотности) Пусть в системе координат Оxyz задано некоторое ограниченное тело U с переменной плотностью  , .

Требуется приближенно вычислить массу этого тела.

Для этого разрежем это тело на n частей _, i = 1, 2, ..., n. Через – обозначим наибольший из диаметров частичных областей. Внутри этой части можем считать что  , где - точка принадлежащая  .

Обозначим объём через , тогда масса одной части  .

А для всего тела: – интегральная сумма.

Затем переходим к пределу при и , i=1,2,...,n и получаем:

Определение 5. Предел сумм интегральной суммы при , если он существует и не зависит от способа разбиения области U на части   и выбора в каждой из них точек  , называется тройным интегралом от функции f(x; y; z) по пространственной области  и обозначается:

7. Если область интегрирования D разбить прямой, параллельной одной из Теорема 1.(Для 2-го и 3-го интеграла одинаково) Если функция интегрируема, то она ограничена.

Теорема 2. Если функция непрерывна в данной (для 3-го интеграла в некоторой замкнутой области) области, то она интегрируема в этой области.