Равносоставленность многоугольников

0:Два многоугольника будем называть равносоставленными, если их можно разрезать на одинаковое число соответственно равных многоугольников

Или

Д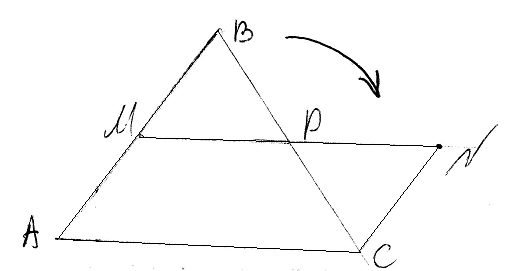 ва многоугольника назыв равносоставленными, если один из них можно разрезать на такие части, из которых, если их сложить другим образом, можно получить второй многоугольник.

Т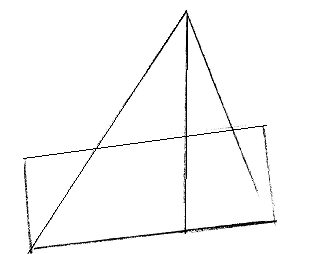 еорема: Всякий треугольник равносоставлен с параллелограммом (одна сторона параллелограмма равна стороне треугольника и высота параллелограмма равна половине соответствующей и высоты треугольника)

Теорема: Всякий треугольник равносоставлен с прямоугольником , основание которого равно одной стороне треугольника, а высота равна половине одной из сторон соответствующей высоты треугольника

Равновеликости многоугольников

Понятие равновеликости явл обобщением понятия равносоставленности .

0: Два многоугольника будем называть равновеликими, если каждому из них можно добавить одинаковое число соответственно равных многоугольников так, что получатся равносильные многоугольники.

Два равносоставленных многоугольника явл равновеликими.

Теорема: Два треугольника, имеющие рывные основания и равные , соответствующие им высоты, равноелики.

Теорема:Параллелограммы с равными основаниями и равными высотами равновелики

Теорема: Если два многоугольника равносоставленны, то они равновеликими

Теорема Бояи – Гервина

Всякие два равновеликих многоугольника явл равносоставленными

11. Топологическое пространство. Топологическое многообразие. Эйлеровая характеристика двумерного многообразия. Теорема Эйлера для многогранников.

Топологическое простраство

Опр: Пусть Х-некоторое не пустое множество будет называть пространство-носитель и пусть некоторое семейство множеств тогда будем говорить, что определяет топологическую структуру или топологию на множестве х, если выполняются следующие условия:

1. Объединение любой системы множеств из 

2. Пересечение конечного числа множеств из 

3. Пусть множество и само множество Х

Множество Х вместе с заданной в нем топологией называется топологическим пространством (Х, )

Элементы из Х называются точками. Множество называется открытым множеством. Любое условие называется аксиомой топологического пространства. На одном том же пространстве можно вводить различные топологические пространства.

Пример:

1. – антидискретная, тривиальная, минимальной топологии;

2. = {всевозможные подмножества множества Х, Х}

называется дискретной или максимальной. Каждая точка пространства Х считается открытым множеством.

3. Каждое метрическое пространство является топологическим пространством.

Многообразие

Пусть (X, ) — топологическое пространство, k-мерной координат­ной системой в этом пространстве называется гомеоморфизм ф неко­торого открытого множества U X на открытое множество число­вого пространства Rⁿ. При этом пару (U, ф) называют k-мерной кар­той, а множество U — координатной окрестностью этой карты.

Если х U, то ф(х) = (х¹, ..., x^k) Rⁿ. Вещественные числа х^k на­зываются координатами точки х в данной карте.

k-мерным топологическим многообразием (или просто k-мерным многообразием) называют отделимое топологическое пространство (X, ) со счетной базой, если это пространство можно покрыть коор­динатными окрестностями k-мерных карт.

В топологии доказывают, что число k (размерность многообра­зия) является топологическим инвариантом, т. е. не меняется при лю­бых гомеоморфизмах пространства

Клеточное разложение.

Обозначим через R+ множество тех точек из R^k(k = 1,2), у ко­торых координата x^k удовлетворяет условию x^k 0. Следователь­но, R+ — это замкнутое полупространство в R^k. Пространство (X, У) называется k-мерным многообразием с краем, если оно отделимо, имеет счетную базу и его точки можно разбить на два непустых класса так, что каждая из точек одного класса (точки внутренние) имеет окрестность, гомеоморфную простран­ству R\ а каждая из точек другого класса (точки краевые) имеет окрестность, гомеоморфную R+, но не имеет окрестности, гомеоморфной R^k.

Множество всех краевых точек называется краем многообра­зия (X, У).

Назовем клеткой любое многообразие с краем, гомеоморфное выпуклому многоугольнику. При этом предполагается, что для дан­ной клетки этот гомеоморфизм фиксирован. Образ вершины мно­гоугольника при этом гомеоморфизме мы назовем вершиной клетки, а образ стороны многоугольника — стороной клетки.

Мы скажем, что двумерное многообразие F разложено на ко­нечное множество клеток F₁, F₂,..., F_n, если выполняются два условия:

1.эти клетки образуют покрытие многообразия F;

2.пересечение любых двух клеток Fi и Fj(i j) либо пусто, либо является вершиной этих клеток, либо стороной каждой из них.

Пусть К — клеточное разложение двумерного многообразия. Точка х F называется вершиной клеточного разложения К, если х — вершина хотя бы од­ной клетки из К. Фигура F называется стороной разложения K, если она является стороной хотя бы одной клетки из К. Введем обозначения: — число вершин, — число сторон, — число клеток разложения K.

Число называется эйлеровой характеристи­кой многообразия F.

Топологическое многообразие.

В топологических преобразованиях меняются многие свойства фигур (длина, площади, прямолинейность). Некоторые более сильные сохраняются.

Теорема Эйлера: Если - число вершин, - число ребер, – число граней простого многогранника, то имеет место равенство:

Док-во: пусть многогранник внутри пустой. Пусть

Одну грань вырежем останется поверхность ее растянем на плоскости.

Число вершин и ребер не изменилось, а граней станет на 1 меньше.

Трианвумеруем (величина не меняется) диагоналями разбиваем на треугольники. 2 типа треугольника: 1. С границей одной стороной; 2) с границей 2 сторонами.

Если отрежем треугольник 1-го типа, число граней уменьшится на 1, вершин на 1.

Если 2-го типа – вершин и граней уменьшится на 1, ребер на 2.

Теорема Эйлера позволяет установить если правильные многогранники.

Существует 5 типов:

Многогранник называется правильным если в гранях его лежит равные правильные многоугольники, а в вершине правильные n-гранные углы, m-угольники в гранях.

- граней; – всего ребер

n-ребер.

- всего ребер;

1. - тетраэдр

2. - куб

3. - октаэдр

4. - икосаэдр

5. - додекаэдр