
- •7. Изображения плоских и пространственных фигур в параллельной проекции. Позиционные и метрические задачи.
- •С войства параллельного проектирования При параллельном проектировании:
- •Изображение треугольника
- •Изображение четырехугольника
- •Правильные пяти и шести угольники
- •Окружность
- •Изображения правильных треугольника и четырехугольника, вписанных в окружность. Квадрат, вписанный в окружность
- •Пирамида
- •9). Система аксиом Вейля трехмерного евклидова пространства, ее непротиворечивость.
- •10. Многоугольники. Площадь многоугольника. Теорема существования и единственности. Равновеликость и равносоставленность. Понятие простого многоугольника
- •Определение площади многоугольника.
- •Теорема существования и единственности площади простого многоугольника. Вычисление площадей прямоугольника, параллелограмма, треугольника, трапеции.
- •Р азличные формулы для площади треугольника
- •Равносоставленность многоугольников
- •Равновеликости многоугольников
- •Теорема Бояи – Гервина
- •11. Топологическое пространство. Топологическое многообразие. Эйлеровая характеристика двумерного многообразия. Теорема Эйлера для многогранников.
- •12. Линии и поверхности в е3. Первая основная квадратичная форма поверхности и её приложения.
9). Система аксиом Вейля трехмерного евклидова пространства, ее непротиворечивость.
2 основн.объекта: вектор и точка; 4 отношения: сумма векторов, произведение вектора на число, скалярное произведение векторов, инцендентность упорядочен.пары точек и векторов; 5 групп аксиом.
I гр. Аксиомы сложения векторов.
Каждым 2-м векторам ставится в соответствие др.вектор, являющийся их суммой так, что вып-ся след.условия:
(
 +
+ )+
)+ =
+(
+
)
=
+(
+
)+ = +
 :
+
:
+ =
=
 ,
,
 :
+
:
+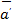 =
=
IIгр. Умножение вектора на число
Каждому вектору и числу ставится в соответствие новый вектор
II1.
1![]() =
=![]()
II2.
![]() )=(
)=(![]() )
)
II3.
(![]() =
= ![]() +
+![]()
II4.
![]() +
+![]() )
=
+
)
=
+![]()
I, IIгр. дают определение векторного пространства.
Далее вводится понятие «линейная комбинация векторов», «линейно зависимая система векторов», «линейно независимая система векторов».
III1. Сущ-т 3 линейно независимых вектора
III2. Всякие 4 вектора явл-ся лин.зависимыми
I-III дают определение 3-х мерного векторного пространства.
Далее вводим понятие базиса векторного пространства, о разложении вектора по данному базису, о единстве разложения.
IV. Каждой паре векторов ставится в соответствие число(скаляр), называемый скалярным произведением векторов так, что при этом вып-ся след.условия:
IV1.
![]() =
=![]()
IV2.
(
)![]() =
=![]() (
)
(
)
IV3.
(
+![]() )=
)=![]() +
+![]()
IV4.
![]() =>
=> ![]() >
>![]() ;
=
;
=
![]()
Опр. Множество векторов, кот.удовл-т аксиомам I-IV групп будем называть 3-х мерным евклидовым векторным пространством.
Если
,
то по IV4
>
=> ![]() =
=![]() - длина
вектора.
- длина
вектора.
Если
![]() ,
то можно ввести величину угла
,
то можно ввести величину угла ![]() =
=![]() ;
если один вектор
,
то угол между векторами неопределен.
;
если один вектор
,
то угол между векторами неопределен.
Опр. Два вектора называются ортогональными, если их скалярное произведение равно 0.
В евклидовом пространстве всегда можно построить ортонормированный базис (векторы, которые попарно ортогональны и их длина равна 1).
V1. Сущ-т по крайней мере одна точка
V2.
Если заданы точки A
и B
в определенном порядке, то существует
единственный вектор
такой, что пара AB
инцендентна вектору
(пару AB
будем обозначать: ![]() )
)
V3.
Если даны точка A
и вектор
,
то ![]() B
такая, что вектор
инцендентен вектору
.
B
такая, что вектор
инцендентен вектору
.
V4.
Для любых трех точек A,B,C
имеет место равенство:
+![]() =
=![]() (аксиома треугольника).
(аксиома треугольника).
I-V – 3-х мерное евклидовое пространство.
Покажем, что система аксиом Вейля является непротиворечивой.
Непротиворечивость системы аксиом Вейля 3-х мерного евклидового пространства.
К любой системе аксиом пред след требования: непротиворечивость, независимость, полнота. Непротивор главное, т.к. все аксиомы получ далее должны удовл ему.
Система аксиом называется непротиворечивой, если существует база, на которой можно задать рассматриваемую структуру рода Т. Чтобы доказать непротиворечивость системы аксиом, достаточно построить какую-либо интерпретацию этой системы аксиом. При построении интерпретации мы должны использовать «достаточно надежные» понятия, относительно которых у нас есть уверенность, что их система внутренне непротиворечива. Только в этом случае можно утверждать, что наша система аксиом А1,А2, …, Аn внутренне непротиворечива, и, значит, в теории Г(Т) мы не получим двух теорем, отрицающих одна другую, как бы далеко мы ни развивали эту теорию.
Вопрос о внутренней непротиворечивости системы аксиом может быть решен только средствами математической логики.
При построении интерпретаций систем аксиом, определяющих структуры, изучаемые в геометрии, мы используем различные числовые множества, считая «наиболее надежными» понятия, взятые из арифметики вещественных чисел. Поэтому при исследовании непротиворечивости системы аксиом А1,А2, …, Аn, не прибегая к средствам математической логики, мы в лучшем случае можем прийти к утверждению такого вида: система аксиом А1,А2, …, Аn непротиворечива, если непротиворечива арифметика вещественных чисел.
Теорию действит.чисел будем считать непротиворечивой. Из объектов этой теории необходимо построить модель, т.е. основным отношениям придать конкретный смысл.
Докажем сначала непротиворечивость 3-х мерного евклид.пр-ва (I-IV).
Под
вектором
будем понимать упорядоченную тройку
вещественных чисел, взятых в определ.порядке
и заключенных в фигурную скобку(![]() {x1,x2,x3}).
{x1,x2,x3}).
Точка – это упорядоченная тройка вещественных чисел, заключенных в круглую скобку(M(x1,x2,x3)).
В скобках записана координата точки или вектора.
Основные
отношения: дано ![]() {x1,x2,x3},
{x1,x2,x3},
![]() {y1,y2,y3}.
{y1,y2,y3}.
 +
+ = { x1+y1,
x2+y2,
x3+y3}
= { x1+y1,
x2+y2,
x3+y3}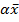 ={
={ x1,
x2,
x1,
x2,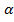 x3}
x3}
 =
{ x1
=
{ x1 y1+
x2
y2+
x3
y3}
y1+
x2
y2+
x3
y3}A(ai), B(bi), {x1,x2,x3}
Пара
AB
и вектор
инцендентны, если ![]() =
= ![]() -
-![]() ,
=1,2,3
,
=1,2,3
{a1,a2,a3},
{b1,b2,b3},
![]() {c1,c2,c3}
{c1,c2,c3}
I1.
(![]() ={
={![]() )
)![]() ;
;![]() )
)![]() ;
;![]() )
)![]() }=
{
}=
{![]() +(
+(![]() +(
+(![]()
![]() +(
+(![]() )
– выполняется.
)
– выполняется.
I2 –вып-ся
I3
:
![]() ,
,
![]()
I4
: ![]() ,
+
,
+![]() =
{
=
{![]()
III1:
![]() покажем,
что векторы линейно зависимы,т.е.
покажем,
что векторы линейно зависимы,т.е.
![]()
Разложение
векторов в базис однозначно => ![]() =>
=>![]() лин.независ.
лин.независ.
III2.
{a1,a2,a3},
{b1,b2,b3},
{c1,c2,c3},
![]() {d1,d2,d3}
{d1,d2,d3}
![]()
 => число неизвестных больше числа
=> число неизвестных больше числа
уравнений => имеет бесчисл.мн-во решений =>лин.завис.
IV. {x1,x2,x3}, {y1,y2,y3}.
IV1:
![]() ,
{
,
{![]()
IV2- вып-ся(ассоциат.закон)
IV3 – вып-ся (по дистриб.закону)
IV4:
![]() ={
={![]() => вып-ся
=> вып-ся
=
=> {![]() =>
=
=>
=
V. 1-4–вып-ся
V3. A(a1, a2, a3), {x1,x2,x3}
(![]() B)
(
B)
(![]() )
)
{b1-a1, b2-a2, b3-a3} – вып-ся
V4. A(ai), B(bi), C(ci), i=1,2,3
{b1-a1, b2-a2, b3-a3}, {c1-b1, c2-b2, c3-b3}, {c1-a1, c2-a2, c3-a3}
![]() {c1-a1,
c2-a2,
c3-a3}=
ч.т.д
{c1-a1,
c2-a2,
c3-a3}=
ч.т.д
След-но все 18 аксиом – справедливые теоремы теории действ-х чисел. Мы построили модель.
Определение прямых, лучей, отрезков, плоскостей.
Из анализа аксиоматики Вейля видно, что она в основном явл-ся векторной.
A,
B – точки,
![]()
Опр.
Множ-во точек M
таких, что ![]() коллинеарен
,
т.е.
коллинеарен
,
т.е. ![]() будем называть прямой
(
будем называть прямой
(![]()
(AM)
={M:![]() ,
где
,
где ![]() ,
A
– нач.точка,
- направляющий вектор прямой.
,
A
– нач.точка,
- направляющий вектор прямой.
Если
![]() => M
совпадает с A;
Если
=> M
совпадает с A;
Если ![]() =>
M=B.
=>
M=B.
Пусть
даны 3 точки: M1(![]() M2(
M2(![]() M3(
M3(![]()
Опр.
Буд.гов., что M2
лежит между M1
и M3,
если M1![]() M2
M2![]() M3
три различные точки и
M3
три различные точки и ![]() .
.
Имея понятие «между» мож.напис.понятие отрезка
Опр. Отрезком буд.наз-ть мн-во точек, сост.из M1,M3 и точек, лежащих между M1 и M3; M1 и M3 – концы отрезка
Опр.
Отрезком
AB
явл-ся
мн-во точек, значение параметра ![]() которых принадл.[0,1].
которых принадл.[0,1].
Опр. Лучом [AB) буд.наз-ть мн-во точек, знач-е параметра кот-х приним.лишь положит.знач-е.
Свойства прямой:
Н
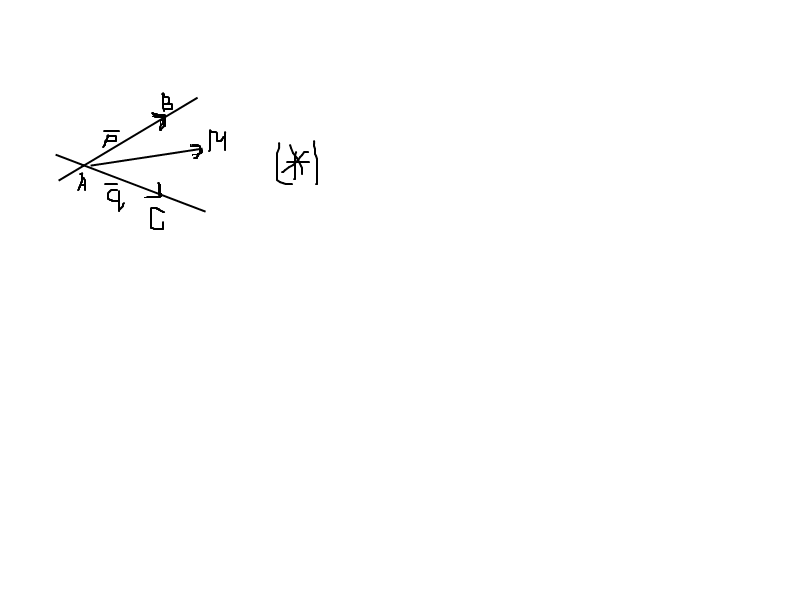 а
прямой
а
прямой  бесчисл.мн-во
точек
бесчисл.мн-во
точекПрямая определ-ся однозначно любыми 2-мя ее разл.точками
Пусть даны 3 разл.точки,не леж.на одной прямой.
Опр.
мн-во точек M
таких, что
= u![]() буд.наз.плоскостью
(u,v
буд.наз.плоскостью
(u,v![]()
(A,B,C)={M:![]() = u
;
u,v
= u
;
u,v![]() }
}
если u,v =0 => M совпад.с A; если u=1 ,v =0 => M совпад. с B; если u =0,v =1 => M совпад.с C.
u,v – параметры, фиксир.точку М.; А-нач.точка; М-текущая точка
св-ва плоскости:
А,В,С принадл.пл-ти
На пл-ти сущ-т бесчисл.мн-во точек, среди них хотя бы одна тройка точек не лежит на одной прямой
Пл-ть вполне опред-ся любыми 3-мя ее неколлин-ми точками
опр.
Если в ур-ии пл-ти u![]() ,
v-произв.зн-е,
то получ.полуплоскость
с
границей АС. (АС,
В)
,
v-произв.зн-е,
то получ.полуплоскость
с
границей АС. (АС,
В)
опр. Пересечение полуплоскостей (АС, В) и (АВ,С) буд. наз-ть углом ВАС
![]() -
векторно-парам.ур-е пл-ти.
-
векторно-парам.ур-е пл-ти.
