7. Изображения плоских и пространственных фигур в параллельной проекции. Позиционные и метрические задачи.

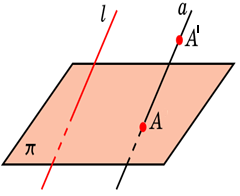
плоскость проекции

l – направление проектирования ( )

А^/ - произвольная точка пространства

Через точку А^/ проведем прямую ∥ l

А – точка пересечения этой прямой с пл – параллельная проекция на пл в направлении l

Прямая АА^/ - проектирующая прямая

0: Точки, имеющие одну и ту же параллельную проекцию назыв. конкурирующими

С войства параллельного проектирования При параллельном проектировании:

1⁰) Проекцией точки есть точка

2⁰)Проекцией прямой является прямая.

Доказательство:

Найдем проекцию А произвольной точки А^/ прямой k^/ и рассмотрим плоскость , проходящую через k^/ и АА^/. Плоскости пересекаются по некоторой прямой k. Докажем что k и есть проекция k^/.

Возьмем произвольную точку В^/ прямой k^/ и в пл проведем прямую ВВ^/ параллельную прямой АА^/. Т.к АА^/ ∥ l и АА^/ ∥ ВВ^/ ⇒ ВВ^/ ∥ l ⇒В – проекция точки В^/ на пл .

Т . о мы доказали что прямая k явл проекцией прямой k^/ на пл

3⁰)Если точка лежит на линии, то ее проекция лежит на проекции этой линии

4⁰)Если прямые параллельны, то их проекции тоже параллельны

5⁰)сохраняются отношения отрезков, лежащих на одной прямой или на

параллельных прямых.

В св – вах ничего не говорится об углах ⇒ величина угла не сохраняется при параллельном проектировании

Изображение плоских фигур в параллельной проекции (треугольник, четырехугольник, правильный n-угольник, круг).

Изображение треугольника

За изображение треугольника можно принять любой треугольник ⇒ за равнобедренный, равносторонний и прямоугольный так же можно принять любой треугольник.

В треугольнике медиана в медиану переходит, а высота в высоту и биссектриса в биссектрису не переходит

Изображение четырехугольника

За изображение параллелограмма может быть принят любой параллелограмм ⇒ за изображение квадрата может быть принят любой параллелограмм

Трапеция перейдет в трапецию

Произвольный четырехугольник (без ∥ сторон) перейдет в произвольный четырехугольник (без ∥ сторон)

Но: трапеция перейдет не в любую трапецию и произвольный четырехугольник перейдет не в любой произвольный четырехугольник т.к должно сохраняться отношение отрезков.

Правильные пяти и шести угольники

И з предыдущего изложения ясно, что при построении изображении n -угольника, три вершины изображения берутся произвольно, а остальные вершины находятся построением с соблюдением условий.

На рисунке построено изображение пятиугольника ABCDE .

Вершины A,B,C выбраны произвольно, а вершины

D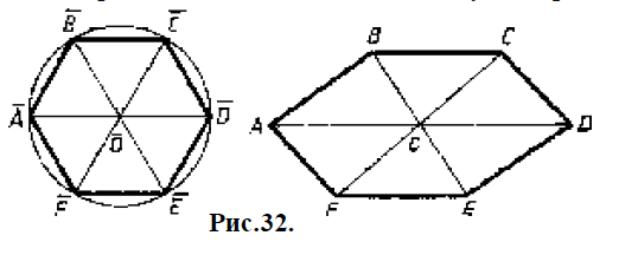 ,E построены. Вершина D , например, построена с использованием условий (BD,M )= (BD,M) и (AC,M )= (AC,M).

На рисунке 32 построено изображение правильного шестиугольника ABCDEF с центром в точке O . В данном случае произвольными выбираем точки A,B,O . Точку D строим как точку, симметричную точке A относительно точки O . Для построения точки C строим прямые BC и DC из условий BC AO и DC BO , и т.д.

Окружность

Построение изображения окружности основано на следующем утверждении:

В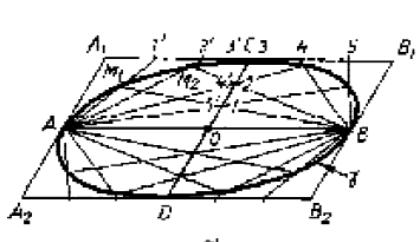 любом аффинном отображении эллипс (окружность) переходит в эллипс.

Т.е окружность переходит в эллипс.

Построение данной окружности сводится к построению какого-нибудь эллипса на плоскости.

Эллипс обычно задается двумя хордами AB и CD , принадлежащими сопряженным диаметрам. Их общей серединой является центр O эллипса. Ход построения изображения окружности: