20 Нэ и их характеристики.

По виду ВАХ нелинейные элементы можно классифицировать на симм. и несимм.

Симм. наз-ся элемент у которого хар-ка не зависит от полярности приложенного напряжения.

НЭ можно разделить на упр-е и неупр-е.

Упр-й элемент имеет дополнит. цепь упр-я воздействуя на которую можно менять вид ВАХ.

21 ) Графический метод расчета нелинейных резистивных цепей.

Графический расчет цепей с параллельным соединением НЭ. Для расчета заданы ВА-характеристики: I₁(U₁), I₂(U₂), I(U). I=I₁+I2

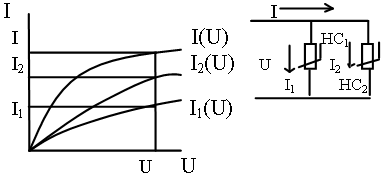
Графический расчет цепей с последовательным соединением НЭ

U=U1+U2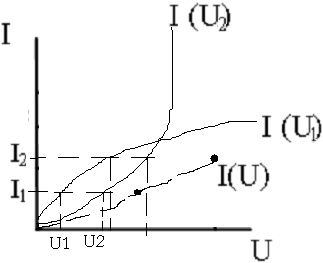

29)Однородная линия, первичные параметры.

Электрические свойства длинной линии характеризуются первичными параметрами, т.е. параметрами, отнесёнными к единице длины линии(1 км в линиях проводной связи и 1м в радиосвязи). Первичными параметрами являются:

резистивное сопротивление единицы длины линии R – это сопротивление проводов линии единичной длинны.

индуктивность единицы длины линии L – определяется отношением магнитного потока, сцепляющегося с контуром единичной длины, к току, вызывающему этот поток. (Гн/км)

ёмкость единицы длины линии C – определяется отношением заряда, приходящегося на ед-цу длины линии, к напряжению между проводами линии.(Ф/км)

проводимость изоляции единицы длины линии G – обусловлена несовершенством изоляции и представляет собой активную составляющую проводимости изоляции между проводами, отнесённую к единице длины линии.

Если первичные параметры остаются пост на протяжении всей ее длины, то линия- однородная.

30)Дифференциальные уравнения однородной линии.

Выделим элементарный участок линии длиной Ах, находящийся на расстоянии х от начала линии

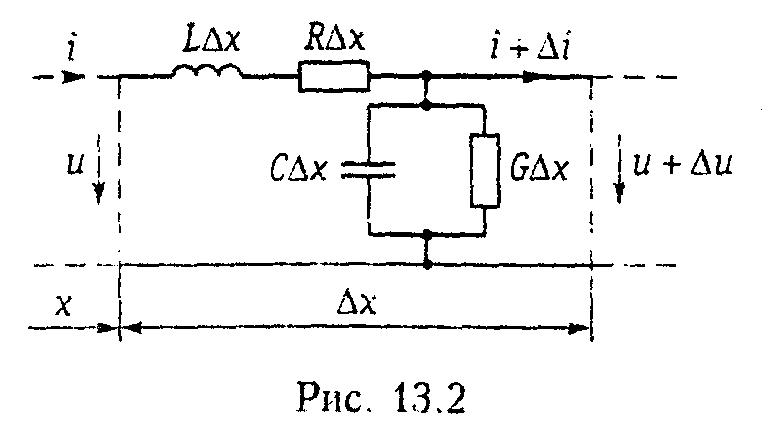
Уменьшение напряжения в конце участка линии Ах по сравнению с его началом вызвано падением напряжения на ин­дуктивности LΔx и сопротивлении RΔx.

X=0

;

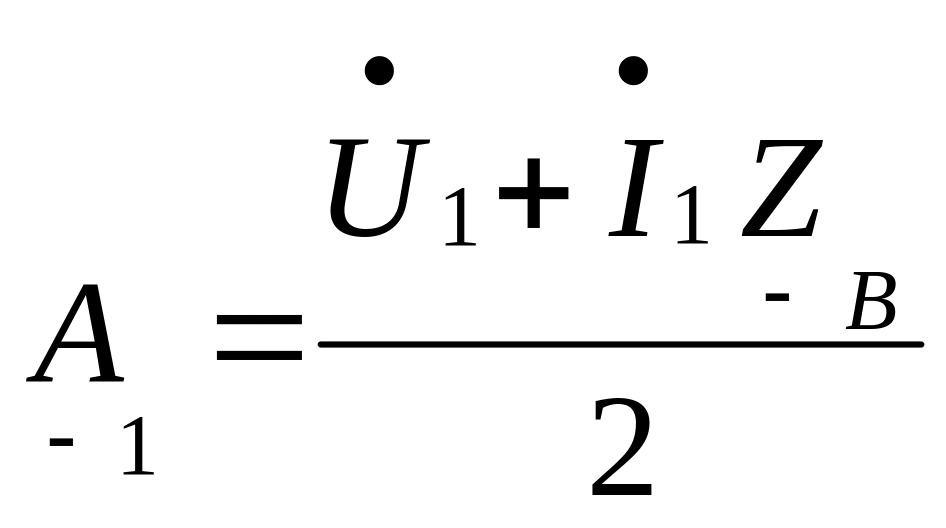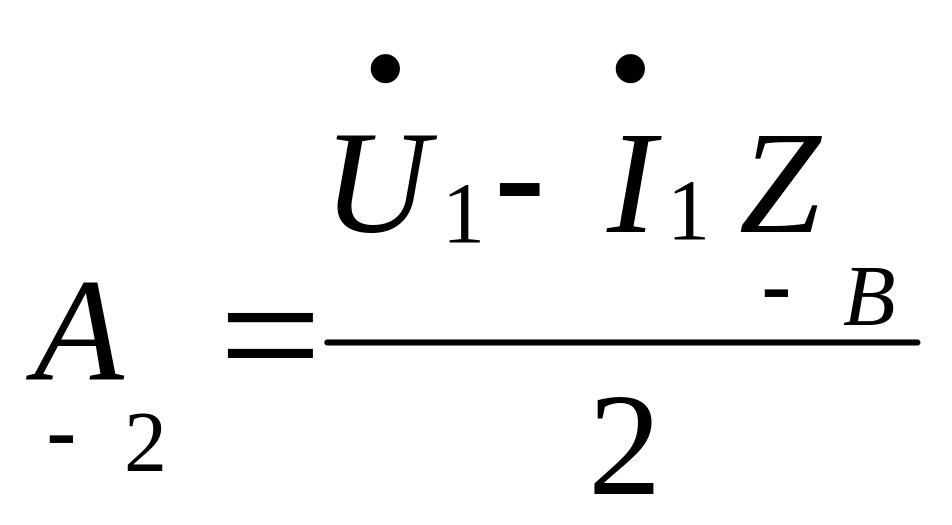
Это есть уравнения передачи однородной длинной линии. Параметры γ и Z_B получили название коэффициента распространения и волнового сопротивления линии.

Если учесть, что

то уравнения передачи можно переписать в более компактной форме:

x=l

32) Вторичные параметры однородной линии.

- активная величина

Линия без потерь - это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R = 0 и G =0.

При анализе процессов, происходящих в линии без потерь, расположение той или иной точки на линии характеризовать ее удалением от конца линии. уравнения передачи линии без потерь

34) Входное сопротивление линии.

Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение для Zb_X. используя уравнения передачи линии

Согласованный режим:

XX:

КЗ:

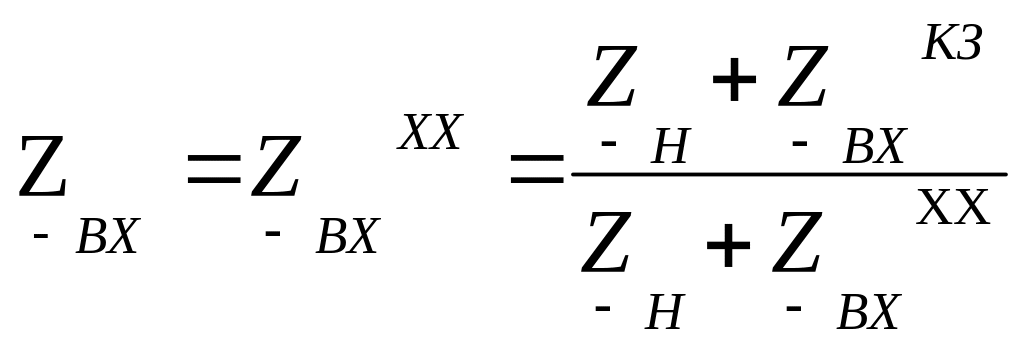
35) Согласованный режим работы линии.

При нагрузке линии без потерь на резистивное сопротивление Z_h = R_H, равное волновому Zb = ρ_в, ток I2 = U₂/Rн = U2/ ρ_в

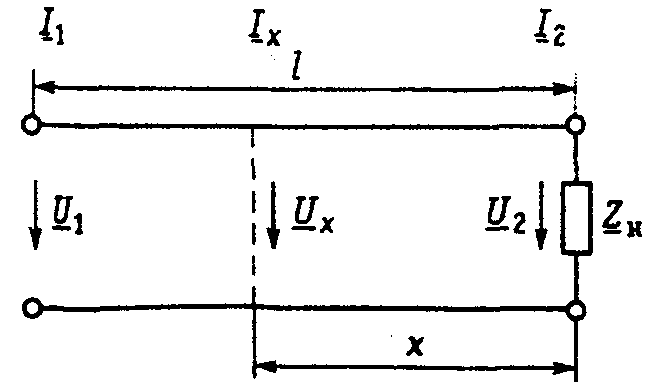
Уравнения передачи:

Таким образом, при согласованном включении линии без потерь в ней существуют только падающие, или бегущие, волны напряжения и тока. При этом амплитуды колебаний постоянны по всей длине линии). Данный режим работы линии называют также режимом бегущей волны. Сдвиг фаз между напряжением и_х и током i_x равен нулю, поэтому энергия бегущей волны носит активный характер.

36 Линия без искажений

есть вещественная константа.

Линия, параметры которой удовлетворяют условию (4), называется линией без искажений.Фазовая скорость для такой линии

и затухание .

37 Линия без потерь

Линией без потерь называется линия, у которой первичные параметры  и  равны нулю. В этом случае, как было показано ранее,  и . Таким образом, ,

откуда .

38)Уравнения линии без потерь

откуда .

40) Стоячие волны в линии без потерь.

Короткое замыкание линии без потерь (режим стоячих волн)

При Z _h=0 напряжение в конце линии U₂ = 0. Уравнения передачи линии:

Если положить для простоты начальную фазу φ_i2 тока в конце линии равной нулю, то мгновенные значения напряжения и тока в любой точке линии описываются выражениями:

Таким образом, в КЗ линии возникают волны напряжения и тока, которые не распространяются вдоль линии, находятся на одном месте. Такие волны называются стоячими, а уравнения передачи - уравнениями стоячих волн. Описываемый режим работы линии получил • также название режима стоячих волн.

Разомкнутая линия без потерь (режим стоячих волн)

В режиме XX Z _h = ∞ и . Уравнения передачи

Сравнивая уравнения передачи с уравнениями КЗ линии, видим, что полученные уравнения так-же являются уравнениями стоячих волн. Разница состоит в том, что узлы и пучности напряжения при XX совпадают с узлами и пучностями тока при коротком замыкании, а узлы и пучности тока разомкнутой линии - с узлами и пучностями напряжения КЗ линии. В конце разомкнутой линии образуется пучность напряжения и узел тока.

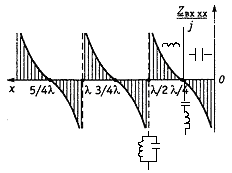
Данный режим работы линии называется режимом стоячих волн. Входное сопротивление разомкнутой линии без потерь определяется

Его график, отражающий зависимость от х,