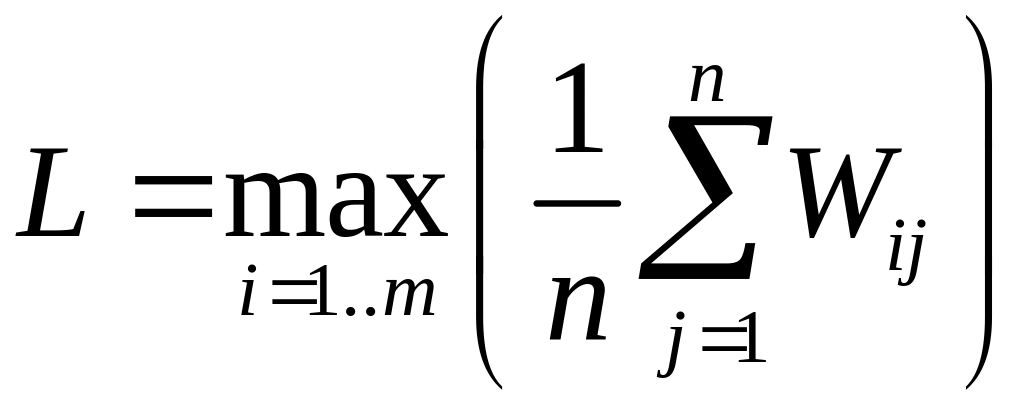Сравнение концепций решения

Чтобы подытожить результаты данной главы, удобно рассмотреть следующий рисунок, показывающий, как соотносятся между собой различные концепции решения некооперативных игр.

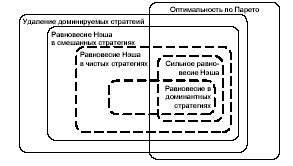
Рис. Сравнение концепций решения некооперативных игр

Области на рисунке представляют собой различные концепции решения. Если одна область включается в другую, значит, первая из них является более «точной», то есть, если первая концепция дает некоторую ситуацию в качестве решения, значит, вторая будет давать эту ситуацию, как одно из решений игры. Сплошной линией на рисунке обведены концепции решения, для которых доказано существование решения для произвольной игры в нормальной форме (для равновесия Нэша в смешанных стратегиях его существование доказано в условиях теоремы 3). Пунктиром обведены концепции, которые для некоторых игр дают пустое множество в качестве решения.

Из рисунка видно, что решение в чистых стратегих и сильное равновесие Нэша являются самыми сильными концепциями решения: из того, что ситуация равновесна в доминантных стратегиях, следует, что она является и равновесием Нэша. Также и из сильной равновесности следует равновесность по Нэшу. Самая слабая концепция – это удаление доминируемых стратегий. Она предлагает в качестве решения самое широкое множество ситуаций. Этот недостаток несколько оправдывается его логической простотой. «Золотой серединой» в некотором роде, является равновесие Нэша в смешанных стратегиях. Выше доказано (см. теорема 3) существование, по крайней мере, одной равновесной ситуации для достаточно широкого класса игр. В то же время, эта концепция достаточно строгая: множество равновесий Нэша обычно гораздо уже, чем можно получить, удаляя доминируемые стратегии. Эти преимущества и определили популярность равновесия Нэша при решении прикладных теоретико-игровых задач. Несколько особняком от других стоит оптимальность по Парето. Рисунок показывает, что, даже просто удаляя доминируемые стратегии, можно получить в результате лишь не оптимальные по Парето исходы (см. пример 11). Причина, по которой это происходит, состоит в том, что в данной главе рассматриваются некооперативные игры, где каждый игрок следует лишь своим интересам, не зная ничего о поведении партнеров. Достижение же оптимальных по Парето ситуаций зачастую требует обмена информацией между игроками, согласования их действий или даже компенсационных выплат некоторым игрокам за выбор ими определенных стратегий.

Глава 4. Игры с неполной информированностью

При определении игры в нормальной форме предполагалось, что на момент выбора стратегий игроки имеют полную информацию о виде функций (матрице) выигрыша других игроков.

Но как описать рациональное поведение игроков в случае, когда они сами не знают точно интересы своих противников? Ответу на этот вопрос посвящен материал настоящей главы «Игры с неполной информированностью».

При принятии решений в условиях неполной информации следует различать ситуацию риска и ситуацию неопределённости. Собственно разница между риском и неопределённостью касается того, знает ли принимающий решение что-либо о вероятности наступления определённых событий.

Риск присутствует тогда, когда вероятности, связанные с различными последствиями принятия решения, могут оцениваться на основе данных предшествующего периода (имеется статистическая информация о подобных ранее принимаемых решениях (о подобных изучаемой ситуациях) т.п.).

Неопределённость существует тогда, когда эти вероятности приходится определять субъективно, т.к. нет данных предшествующего периода (нет соответствующей статистики). Задача выбора решения в условиях неопределённости сводится к следующему.

Пусть задан некоторый вектор S = (S₁,S₂,..,S_n), описывающий n состояний внешней среды, и вектор X = (X₁,X₂,..,X_m), описывающий m допустимых решений. Требуется найти такой вектор X^* =(0,0,..,0, X_i ,0,..,0), который бы обеспечивал оптимум некоторой функции полезности W(X,S) по некоторому критерию K.

Значение оптимума функции W(X,S) раскрывается, исходя из постановки конкретной задачи (к примеру, если обсуждается получение прибыли, то значение функции стремятся максимизировать, если себестоимость – минимизировать).

Информацию об указанной функции полезности (по сути исходные данные задачи такого типа) представляют матрицей размерности m  n c элементами W_ij = F(X_i,S_j), где F - решающее правило (определяемое из постановки конкретной задачи).

Следует отметить, что формирование решающего правила во многом предопределяет конечный результат расчетов (в случае его неточности или ошибок даже правильный выбор критерия оптимальности и соответствующие расчеты не дают основания считать принятое решение наилучшим).

При достаточно четкой экономической постановке задачи практически не возникает проблем с формированием матрицы {W_ij }.

Критерий принятия решения в ситуации риска. Предположим, что в нашем распоряжении имеются статистические данные, позволяющие оценить вероятность того или иного состояния внешней среды, и этот опыт может быть использован для оценки будущего. При известных вероятностях P_j для возникновения состояния S_j можно найти математическое ожидание W(X,S,P) и определить вектор X^* , обеспечивающий

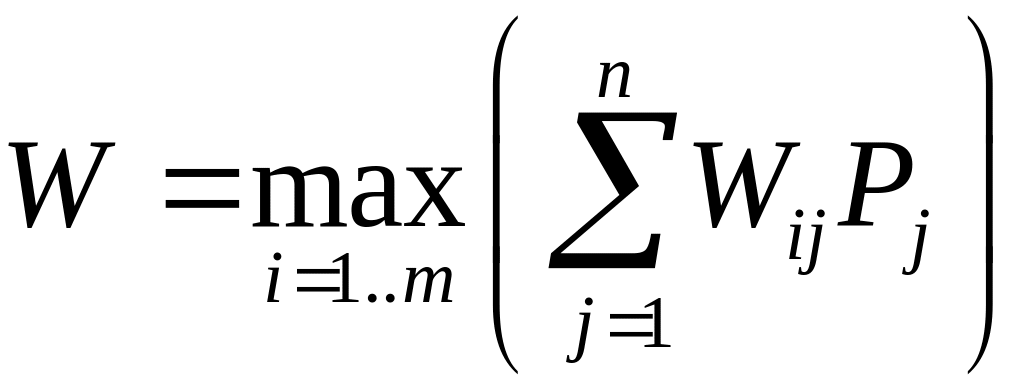
Критерии принятия решения в ситуации неопределенности достаточно многообразны.

Критерий Лапласа. По принципу недостаточного основания в условиях, когда невозможно выяснить вероятности для возникновения того или иного состояния внешней среды, им сопоставляют равные вероятности, находят средний эффект для каждого из рассматриваемых вариантов решения и выбирается тот из них, где средний эффект максимален: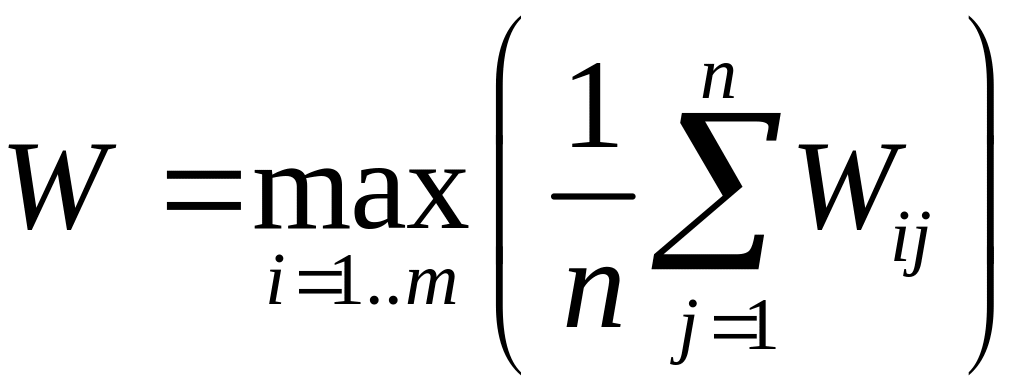

Критерий Вальда (критерий наибольшей осторожности/ пессимиста). Для каждого из рассматриваемых вариантов решения X_i выбирается самая худшая ситуация (наименьшее из W_ij) и среди них отыскивается гарантированный максимальный эффект:

Критерий Гурвица. Ориентация на самый худший исход является своеобразной перестраховкой, однако опрометчиво выбирать и излишне оптимистичную политику. Критерий Гурвица предлагает некоторый компромисс:

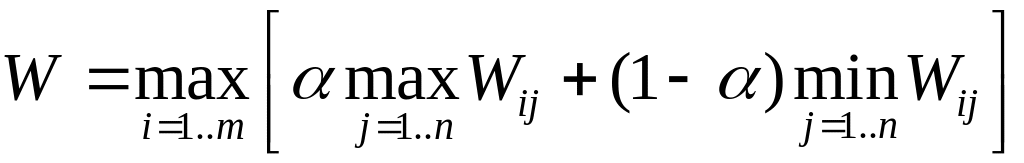
где параметр  принимает значение от 0 до 1 и выступает как коэффициент оптимизма. К примеру, при  =0 (полный пессимизм) критерий Гурвица превращается в критерий Вальда, при  =0.5 мы расцениваем равновероятно шансы на успех и неудачу, при  =0.2 мы более осторожны и вероятность успеха считаем меньшей (0.2) чем возможную неудачу.

Критерий Сэвиджа. Суть его - нахождение минимального риска. При выборе решения по этому критерию:

 матрице функции полезности (эффективности) сопоставляется новая матрица - матрица сожалений , элементы которой отражают убытки от ошибочного действия, т.е. выгоду, упущенную в результате принятия i-го решения в j-м состоянии;

 по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления

Вполне логично, что различные критерии приводят к различным выводам относительно наилучшего решения. Вместе с тем возможность выбора критерия дает свободу лицам, принимающим экономические решения (если они, конечно, располагают достаточными средствами для постановки подобной задачи). Любой критерий должен согласовываться с намерениями решающего задачу и соответствовать его характеру, знаниям и убеждениям.

Принятие решения в ситуации риска (критерий Байеса)
Лапласа		Гермейера (осторожного пессимизма)
Вальда (крайнего пессимизма)		Максимаксный (крайнего оптимизма)
Гурвица		Ходжа-Лемана
Произведений		Сэвиджа	, где

ПРИМЕР. В приморском городе решено открыть яхт-клуб. Сколько следует закупить яхт (из расчета: одна яхта на 5 человек), если предполагаемое число членов клуба колеблется от 10 до 25 человек. Годовой абонемент стоит 100 денежных единиц. Цена яхты - 170 денежных единиц. Аренда помещения и хранение яхт обходится в 730 денежных единиц в год.

Решение. Несомненно, что имеет смысл рассматривать количество приобретаемых яхт в диапазоне от двух до пяти (4 варианта) и количество потенциальных яхтсменов от 10 до 25. Однако объем перебора будет великоват и потому ограничимся вариантами 10, 15, 20, 25 (если полученные выводы для смежных вариантов будут существенно разниться, проведем дополнительный, уточняющий расчет). Итак:

х={x_i}=(2,3,4,5) – количество яхт ( i = 1,2,3,4);

S = { S_j} =( 10, 15, 20, 25) – количество членов яхт-клуба ( j = 1,2,3,4).

Для того, чтобы начать поиск решения, построим матрицу полезности, элементы которой показывают прибыль при принятии i -го решения при j –ом количестве членов яхт-клуба:

W_ij = 100  min(5x_i ; S_j) - 170x_i - 730

т.е. решающее правило в нашей задаче формулируется как «доход–затраты».

Выполнив несложные расчеты, заполним матрицу полезности {W_ij}:

	S1 = 10	S2 = 15	S3 = 20	S4 = 25
x1 = 2	-70	-70	-70	-70
x2 = 3	-240	260	260	260
x3 = 4	-410	90	590	590
x4 = 5	-680	-80	420	920

Например, W₁₁ = 100  min(5  2, 10) - 170 2 -730 = -70

W₁₂ = 100  min(5  2, 15) - 170 2 -730 = -70

W₁₃ = W₁₄ = -70 (спрос на яхты останется неудовлетворенным). Отрицательные значения показывают, что при этих соотношениях спроса на яхты и их наличия яхт-клуб несет убытки.

Критерий принятия решения в ситуации риска. Предположим, что есть статистические данные, позволяющие оценить вероятность того или иного спроса на членство в яхт-клубе: Р = ( 0,1 ; 0,2 ; 0,4 ; 0,3). Тогда математическое ожидание величины прибыли для каждого из рассматриваемых вариантов решения (предложение яхт в яхт-клубе):

W1 = (-70 0,1)+(-70 0,2)+(-70 0,4)+(-70 0,3) = -70 ,

W2 = (-240 0,1)+(260 0,2)+(260 0,4)+(260 0,3) =210;

W3 = 390;  W4 = 370.

Вывод: в условиях рассматриваемой ситуации наиболее целесообразно закупить 4 яхты (в этом случае максимальная ожидаемая прибыль яхт-клуба составит 390 денежных единиц).

Принятие решения в ситуации неопределенности.

А. Для применения критерия Лапласа находим:

W1 = ((-70)+(-70)+(-70)+(-70)) / 4 = -70 ;

W2 = ((-240)+(260)+(260)+(260)) / 4 =135;

W3 = 215;  W4 = 170.

Вывод: в условиях равновероятности возникновения той или иной величины спроса на членство в яхт-клубе следует закупить 4 яхты и при этом можно рассчитывать на прибыль в размере 215 д.е.

Б. Критерий Вальда (выбор осторожной, пессимистической стратегии) - для каждой альтернативы (количество яхт в клубе) выбирается самая худшая ситуация (наименьшее значение величины прибыли) и среди них отыскивается гарантированный максимальный эффект: = max (-70; -240; -410; -580) = -70

Вывод: принимая решение по критерию Вальда, яхт-клубу следует закупить 2 яхты и максимум ожидаемого убытка не превысит 70 д.е.

В. Критерий Гурвица (компромиссное решение между самым худшим исходом и излишне оптимистическим). Рассмотрим изменение решения нашей задачи в зависимости от значений коэффициента оптимизма (в таблице выделены значения, удовлетворяющие критерию Гурвица при различных  ):

	 = 0,2	 = 0,5	 = 0,8
x1 = 2	-70	-70	-70
x2 = 3	-140	10	160
x3 = 4	-210	90	390
x4 = 5	-380	170	620

Вывод: при  0,5 следует закупить 5 яхт и ожидать прибыль порядка, не меньшую 170 д.е. (надеемся на широкую популярность нашего клуба и определенную финансовую состоятельность любителей), при  = 0,2 не следует закупать более 2 яхт (мы более осторожны в своих прогнозах и, скорее всего, предпочтем отказаться от создания клуба).

Г. Критерий Сэвиджа (нахождение минимального риска). При выборе решения по этому критерию сначала матрице полезности сопоставляется матрица сожалений D - для нашего примера, вычитанием (-70) из первого столбца матрицы полезности, 260 из второго столбца, 590 и 920 из третьего и четвертого столбцов соответственно:

	S1 = 10	S2 = 15	S3 = 20	S4 = 25
x1 = 2	0	-330	-660	-990
x2 = 3	-170	0	-330	-660
x3 = 4	-340	-170	0	-330
x4 = 5	-510	-340	-170	0

Наибольшее значение среди минимальных элементов строк (выделенные в таблице значения) равно: = max(-990; -660; -340; -510) = -340

Вывод: покупая 4 яхты для открываемого яхт-клуба, мы уверены, что в худшем случае убытки клуба не превысят 340 д.е.

Общий вывод. Рассмотренные критерии приводят к различным решениям и дают тем самым информацию к размышлению (принятое решение здесь будет существенно зависеть от психологии и интуиции субъекта решения).

Неточную информацию о функциях выигрыша игроков принято описывать с помощью понятия типа игрока. Рассмотрим следующую игру n лиц, в которой каждый из игроков имеет некоторый тип r_i  _i из множества _i возможных типов данного игрока i. Будем считать, что все множества типов _i компактны, iN. Функции выигрыша игроков F_i = F_i(x₁, …, x_n, r₁,…,r_n)зависят как от действий x_iX_iвсех игроков, так и от их типов r_i_i, iN.

Определение: Профилем типов игроков называется вектор

r = (r1, r2, …, rn)  .

Принцип максимального гарантированного результата

Принцип максимального гарантированного результата (МГР)

МГР - это один из самых общих принципов принятия решений в условиях интервальной неопределенности. В соответствии с принципом МГР неопределенность устраняется введением предположения, что неопределенные параметры принимают наихудшие для ЛПР значения.

Пусть игровая ситуация с точки зрения i-го игрока определяется вектором z = (y_i, q, r), y_iA_i, q , r , и его выигрыш F_i = F_i(z) зависит от ситуации. Пусть y_i A_i – действие i-го игрока, и на момент принятия игроком решения о выборе стратегии ему известны значения параметров q . Об остальных параметрах информации не ожидается. Тогда принцип МГР предлагает использование, так называемой, гарантирующей стратегии.

Определение: Гарантирующая стратегия i-го игрока – это стратегия, определяемая по формуле:

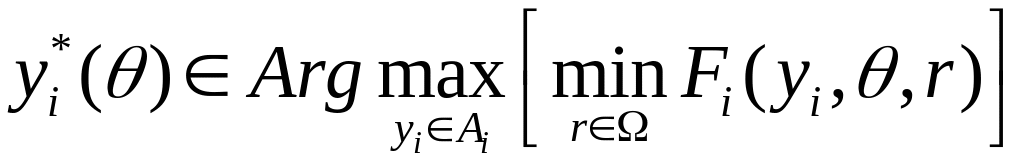
Другими словами, для того, чтобы найти гарантирующую стратегию i-го игрока, необходимо при фиксированных известных параметрах q найти минимум функции выигрыша по неизвестным параметрам r , а затем максимизировать результат минимизации выбором действия y_i. Стратегия y_i*(), на которой достигается максимум, и будет гарантирующей.

Вектор (y_i*() )_iN гарантирующих стратегий игроков называется максиминным равновесием.

Неизвестные параметры могут иметь очень широкое содержательное наполнение: от информации о действиях других игроков, о виде их целевых функций, до информации о правилах игры.

Рассмотрим с этой точки зрения игру с неполной информацией.

Пусть на момент принятия решения каждому игроку известен его тип r_i _i, неизвестны типы других игроков r_j _j (j i) и их стратегии. Если F_i(y₁, …, y_n, r₁, …, r_n) – функция выигрыша i-го игрока, то его гарантирующей стратегией будет стратегия

Можно заметить, что приведенное определение подходит и для игр с полной информированностью – гарантирующей стратегией i-го игрока в игре с полной информированностью будет стратегия

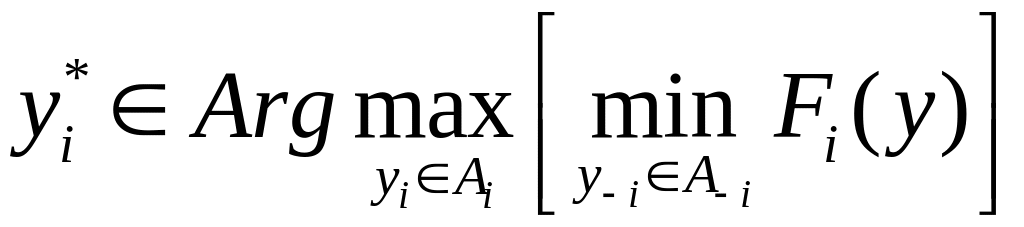
Для существования гарантирующей стратегии достаточно ограниченности функции выигрыша игрока и компактности множеств стратегий A_i и множеств типов игроков _i [21], поэтому можно говорить, что гарантирующие стратегии существуют «почти всегда».

Еще одним преимуществом МГР является то, что для вычисления гарантирующей стратегии игрока i достаточно знать только функцию его выигрыша, и не нужно знание функций выигрыша других игроков.

Недостатком МГР является его чрезмерная пессимистичность. МГР призывает игрока рассчитывать на наихудшее для него поведение противников. Это оправданно в случае антагонистических игр, но, если игрок знает, что интересы противников лишь ненамного отличаются от его интересов, предположение о том, что рациональные противники будут выбирать наихудшее для него действие, не всегда адекватно.

Байесовы игры, равновесие Байеса

Если принцип МГР используется в случае интервальной неопределенности, то ситуация, в которой, помимо знания множества возможных типов противников, каждый игрок знает вероятность реализации того или иного профиля их типов, соответствует игре в форме Байеса (или байесовой игре). Байесова игра формально определяется следующим образом [82].

Пусть имеется n игроков. Игрок i имеет тип r_i _i, принадлежащий множеству возможных типов _i данного игрока. Каждый игрок знает все множества {_i}, а также функцию представлений, (или, иначе, вер) игрока p_i(r_-i|r_i), описывающую плотность условной вероятности появления некоторого сочетания (профиля) типов других игроков в зависимости от типа игрока i. Функции выигрыша F_i(y₁, …, y_n, r₁, …, r_n)зависят как от действий y_i A_i всех игроков, так и от их типов r_i_i, и известны всем игрокам.

Определение: Игра в форме Байеса задается следующей системой: )} ( ),..., ( ); ( ),..., ( ; ,..., ; { 1 1 1 n n n K K p p N .

Рассмотренный выше пример «Аукцион» представляет собой игру в форме Байеса. В этом примере каждый из двух игроков знает функцию выигрыша противника с точностью до некоторого параметра.

Каким же будет рациональное поведение игроков в условиях байесовой игры, ведь игроки должны наилучшим образом использовать имеющуюся в их распоряжении информацию? Ответ на этот вопрос дает концепция равновесия Байеса. Стратегией игрока i в данной игре будем считать распределение ) | ( i i i i r y h h условной вероятности выбора действия yi при условии, что тип игрока равен ri. Тогда равновесием Байеса считается такой набор стратегий (.)) ..., (.), (.), ( 2 1

B

n

B B h h h , что для любого игрока i и любого его типа ri i стратегия (.) B

i h максимизирует по (.) i h функционал







i X i j

i j j

B

j i i i i i i i i i i i dr dy r y r y r r p r r y y K ) ( ) ( ) ( ) , , , ( h h ,

представляющий собой ожидаемый выигрыш игрока i с учетом его

субъективного представления о типах других игроков.

В этом определении решением считается, по сути, набор

смешанных стратегий. Можно переопределить равновесие Байеса

для чистых стратегий. Тогда стратегией будем считать функцию

yi = hi(ri), которая предписывает игроку действие yi в зависимости

от его типа ri i. В этом случае равновесие Байеса определяется

набором стратегий )) ( ..., ), ( ), ( ( 2 1 B

n

B B h h h , таким, что для любого

игрока i и любого его типа ri i стратегия ) ( i

B i r h максимизирует по hi функционал

Рис. 8. Игра с неполной информацией

Равновесие Байеса является обобщением равновесия Нэша в смешанных стратегиях на случай байесовых игр. На самом деле, оно представляет собой равновесие Нэша игры, в которой неполная информация о целевых функциях игроков заменена на неполную информацию о ходе природы. Д. Харшаньи [75] предложил считать, что в начале байесовой игры природа (или другие внешние обстоятельства) определяет типы игроков. После этого игроки должны, зная свой тип, но не зная типов противников, выбрать стратегию (см. рисунок 8).

Представление этой игры в развернутой форме для двух игроков, каждый из которых имеет два возможных типа (r11, r12 для первого игрока, r21, r22 - для второго), и два возможных действия (y11, y12 – у первого игрока, y21, y22 – у второго) приведено на рисунке 8. Для нахождения равновесий байесовой игры необходимо