III. Сведение решения матричной игры к паре двойственных задач линейного программирования.

Сведение решения матричной игры к задачам линейного программирования - наиболее эффективный прием, позволяющий использовать алгоритм симплекс-метода.

Без потери общности будем предполагать, что значение матричной игры  положительно. Согласно следствию теоремы 4.2’, оно представимо в виде

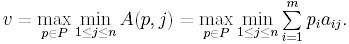
Введем вспомогательную переменную u и запишем задачу нахождения максимина как задачу линейного программирования где

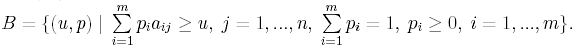
Действительно, при фиксированном p  P максимальное значение u при ограничениях (u,p)B равно

Поскольку  > 0, можно считать, что u принимает положительные значения. Сделаем замену переменных z_i = p_i/u, z = (z₁, ..., z_m). Тогда, учитывая ограничения (u, p)  B, получим

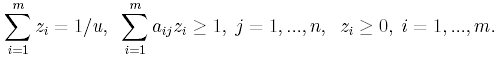
Отсюда

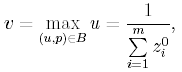
где z⁰ - оптимальное решение задачи линейного программирования

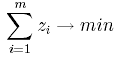
(I)

По z⁰ находим значение игры и оптимальную смешанную стратегию первого игрока:

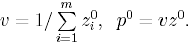
Аналогично можно получить, что

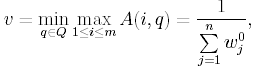
где ⁰ - оптимальное решение задачи линейного программирования

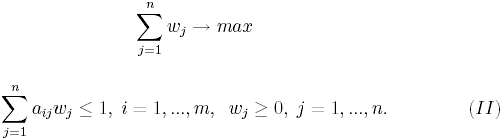
Здесь q⁰ = ⁰ - оптимальная смешанная стратегия второго игрока. Задачи (I) и (II) двойственны одна по отношению к другой.

Отметим свойство дополняющей нежесткости для оптимальных решений z⁰ и ⁰ задач (I) и (II) :

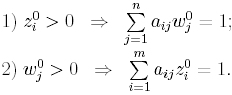
Оно непосредственно вытекает из утверждения теоремы 4.3’ после замены переменных p⁰=z⁰, q⁰ = ⁰.

П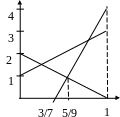 ример 5.3. Решить игру с матрицей . Отметим, что стратегия p = (1/2, 1/2) обеспечивает первому игроку положительный выигрыш. Поэтому >0. Выпишем задачи линейного программирования

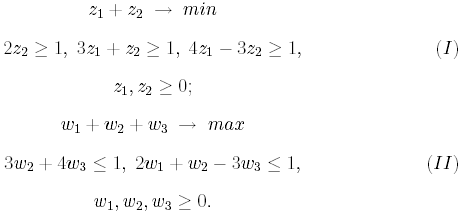
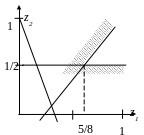
Используя графические построения на плоскости, нетрудно найти, что z⁰ = (5/8, 1/2) - оптимальное решение задачи (I). Отсюда

Найдем оптимальное решение ⁰ задачи (II). Поскольку и , по свойству дополняющей нежесткости

Поэтому

Глава II. Игры двух лиц

9. Ситуации равновесия в играх двух лиц

Понятие антагонистической игры можно значительно расширить. В игре двух лиц интересы игроков необязательно бывают противоположными. Рассматривают и игры многих лиц. Им посвящена третья глава.

Определим игру двух лиц. Пусть первый игрок имеет в своем распоряжении стратегии x из множества стратегий X, а второй игрок - стратегии y из множества стратегий Y. Будем рассматривать игру в нормальной форме. Это означает, что каждый из игроков выбирает стра-

тегию, не зная выбора партнера. Пару стратегий (x, y) будем называть ситуацией. У первого игрока имеется функция выигрыша F(x,y), а у второго - функция выигрыша G(x,y), определенные на множестве всех ситуаций XY. Каждый игрок стремится, по возможности, максимизировать свою функцию выигрыша. Таким образом, игра двух лиц в нормальной форме задается набором Г = <X, Y, F(x,y), G(x,y)>.

В антагонистической игре понятие решения мы связывали с седловой точкой функции выигрыша первого игрока. В произвольной игре двух лиц аналогом седловой точки является понятие ситуации равновесия.

Определение. Ситуация (x⁰, y⁰) называется ситуацией равновесия (равновесием по Нэшу) игры Г, если

Стратегии x⁰ и y⁰, составляющие ситуацию равновесия, будем называть равновесными. Если оба игрока придерживаются ситуации равновесия, то одному игроку от нее невыгодно отклоняться.

y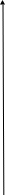

Равновесие по Нэшу

y₁

x

x₁

Пример A. Семейный спор: две точки равновесия (x₁,y₁) и (x₂,y₂).

F / G	y1	y2
x1	1 ; 2	0 ; 0
x2	0 ; 0	2 ; 1

1. Находим наиболее выгодную стратегию первого игрока: x⁰=x₂. По значениям G(x⁰,y₁) и G(x⁰,y₂) выбираем наиболее выгодную стратегию второго игрока: y⁰=y₂. Т.к. F(x₁,y⁰)<F(x⁰,y⁰) и G(x⁰,y₁)<G(x⁰,y⁰), то точка (x₂,y₂) есть точка равновесия.

2. Находим наиболее выгодную стратегию второго игрока: y⁰ = y₁. По значениям F(x₁,y⁰) и F(x₂,y⁰) выбираем наиболее выгодную стратегию первого игрока: x⁰=x₁. Т.к. F(x₂,y⁰)<F(x⁰,y⁰) и G(x⁰,y₂)<G(x⁰,y⁰), то точка (x₁,y₁) есть точка равновесия.

Пример Б. Дилемма заключенных: нет точек равновесия.

F / G	y1	y2	max G
x1	5 ; 5	-1 ; 6	6
x2	6 ; -1	0 ; 0	0
max F	6	0

1. Находим наиболее выгодную стратегию первого игрока: x⁰=x₂. По значениям G(x⁰,y₁) и G(x⁰,y₂) выбираем наиболее выгодную стратегию второго игрока: y⁰=y₂. Т.к. F(x₁,y⁰)>F(x⁰,y⁰) и G(x⁰,y₁)>G(x⁰,y⁰), то точка (x₂,y₂) не точка равновесия.

2. Находим наиболее выгодную стратегию второго игрока: y⁰=y₂. По значениям F(x₁,y⁰) и F(x₂,y⁰) выбираем наиболее выгодную стратегию первого игрока: x⁰=x₂. Т.к. F(x₁,y⁰)>F(x⁰,y⁰) и G(x⁰,y₁)>G(x⁰,y⁰), то точка (x₂,y₂) не точка равновесия.

Упражнение 9.1. Если F(x, y)  -G(x, y), то игра Г - антагонистическая. Докажите, что в антагонистической игре ситуации равновесия - это седловые точки функции F(x, y) на XY.

Обсудим, как можно использовать понятие равновесия по Нэшу с точки зрения принятия решений. В теории игр, как и во многих других теориях, можно выделить два подхода: нормативный и позитивный. Нормативный подход состоит в том, что теория дает рекомендации, как следует действовать в той или иной конфликтной ситуации. А при позитивном подходе теория пытается описать, как на самом деле происходит взаимодействие между игроками. Изначально теория игр развивалась как нормативная. И сейчас мы обсудим понятие равновесия по Нэшу именно с такой точки зрения. В этом случае правило принятия решения можно сформулировать следующим образом: в конфликтной ситуации, описываемой игрой в нормальной форме, каждому участнику следует использовать стратегию, которая входит в равновесие по Нэшу. Позитивный подход обсуждается в конце §10.

Ситуация равновесия в произвольной игре двух лиц может не обладать теми свойствами, которые характерны для седловой точки антагонистической игры.

В антагонистической игре, имеющей решение, компоненты седловой точки являются максиминной и минимаксной стратегиями игроков и, наоборот, любая пара таких стратегий образует седловую точку. Таким образом, в антагонистической игре принцип равновесия согласуется с принципом оптимизации игроками своих гарантированных результатов. Кроме того, во всех седловых точках выигрыш первого игрока один и тот же и равен значению игры. К сожалению, в общем случае ситуации равновесия не обладают указанными свойствами. Убедимся в этом на примерах. Предварительно введем понятие биматричной игры.

Определение. Игра двух лиц Г называется биматричной, если множества стратегий игроков конечны:

X = {1, ...,m}, Y = {1, ..., n}.

Здесь iX, jY - стратегии первого и второго игроков. Выигрыши игроков задаются двумя матрицами

A = (F(i, j))_mn = (aij)_mn, B = (G(i, j)) _mn = (bij) _mn .

Запишем определение ситуации равновесия в обозначениях биматричной игры.

Определение. Ситуация (i⁰, j⁰) биматричной игры Г называется ситуацией равновесия (равновесием по Нэшу), если

Всегда ли в игре двух лиц существует ситуация равновесия? В общем случае ответ - отрицательный, поскольку, например, в антагонистической игре не всегда существует седловая точка.

Приведем пример неантагонистической игры, не имеющей ситуации равновесия.

Пример 9.1. Покупатель (игрок 2) приходит на рынок за яблоками. Продавец, торгующий яблоками (игрок 1), использует пружинные весы. У него есть две стратегии:

1) честно взвесить 1 кг яблок;

2) подкрутить пружинку и обвесить покупателя на 200 грамм.

Назовем эти стратегии "честность"и "обман"соответственно. Покупатель также имеет две стратегии:

1) поверив продавцу, заплатить деньги и уйти;

2) взвесить купленные яблоки на контрольных весах и в случае обнаружения обмана звать кого-то и доказывать, что его обвесили.

Назовем эти стратегии "поверить"и "проверить"соответственно.

Определим выигрыши продавца и покупателя в каждой ситуации:

а) Продавец честно взвесил, а покупатель ему поверил. Соответствующие выигрыши обоих, равные 0, выберем в качестве начала отсчета.

б) Продавец обманул, а покупатель ему поверил. Выигрыш продавца равен 1, так как он получил дополнительную прибыль. Выигрыш покупателя равен -1, поскольку он получил меньше яблок.

в) Продавец честно взвесил, а покупатель его проверил. Выигрыш продавца равен 0. Выигрыш покупателя равен -1/2: он, во-первых, зря потратил время, а, во-вторых, глупо себя чувствует.

г) Продавец обманул, а покупатель его проверил. Выигрыш продавца равен -1, так как обнаружение обмана грозит ему определенными неприятностями (например, его могут лишить лицензии на торговлю на этом рынке). Выигрыш покупателя равен 1/2, так как, во-первых, ему возместили обвес, а, во-вторых, он испытывает моральное удовлетворение от разоблачения обманщика.

Получается следующая биматричная игра:

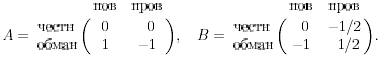
Легко проверить, что здесь нет равновесий по Нэшу.

1. Находим наиболее выгодную стратегию первого игрока: x⁰=x₂. По значениям G(x⁰,y₁) и G(x⁰,y₂) выбираем наиболее выгодную стратегию второго игрока: y⁰=y₂. Т.к. F(x₁,y⁰)>F(x⁰,y⁰) и G(x⁰,y₁)<G(x⁰,y⁰), то точка (x₂,y₂) не точка равновесия.

2. Находим наиболее выгодную стратегию второго игрока: y⁰=y₂. По значениям F(x₁,y⁰) и F(x₂,y⁰) выбираем наиболее выгодную стратегию первого игрока: x⁰=x₁. Т.к. F(x₂,y⁰)<F(x⁰,y⁰) и G(x⁰,y₁)>G(x⁰,y⁰), то точка (x₁,y₂) не точка равновесия.

В приведенном примере элементы матриц A и B удовлетворяют следующим неравенствам:

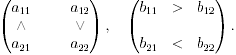
Упражнение 9.2. Проверить, что если элементы в матрицах выигрышей игроков связаны такими соотношениями, то в игре не существует равновесий по Нэшу.

Игры, подобные примеру 9.1, распространены в моделях, описывающих экономические и экологические взаимодействия. Рассмотрим пример игры, имеющей две ситуации равновесия.

Пример 9.2. Игра "семейный спор":

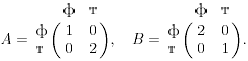
Интерпретация. Жена и муж (первый и второй игроки) обсуждают вопрос, куда пойти развлечься: на футбол (стратегия 1 ) или в театр (стратегия 2). Если идут на футбол, то жена получает 1 единицу, а муж - 2 единицы "удовольствия."Если идут в театр, то выигрыш жены - 2, а мужа - 1. Если оба идут в разные места, то выигрыши игроков - нулевые.

В игре существует две ситуации равновесия: (1,1) и (2,2). Первая из них предпочтительней второму игроку, а вторая - первому. Если игроки будут действовать независимо, то первый выберет стратегию 2, а второй - стратегию 1. В результате оба получат по нулю. Пример 9.2 показывает, что необходим какой-то механизм координации при выборе стратегии, если существует несколько равновесий по Нэшу. Поэтому игры, подобные примеру 9.2, называют также "играми на координацию".

Использование ситуаций равновесия на практике часто связывается со следующим сценарием поведения игроков. Они сначала должны договориться о ситуации равновесия, затем всякие переговоры запрещаются и игроки независимо выбирают свои стратегии, возможно нарушая принятое соглашение. Заметим, что одному игроку будет невыгодно отклоняться от своей равновесной стратегии. Если игроки придерживаются в игре такого сценария поведения, то игра Г называется бескоалиционной.

Приведем еще один пример "игры на координацию".

Пример 9.3. Игроками являются два водителя, которым надо проехать через перекресток, к которому они подъехали одновременно. Есть две стратегии пересечения перекрестка: использовать "правило правой руки", согласно которому водитель должен пропустить помеху справа (стратегия 1), или "правило левой руки", согласно которому водитель должен пропустить помеху слева (стратегия 2). Если оба водителя придерживаются одного правила, то они успешно разъедутся, но если один из них использует "правило правой руки", а другой "правило левой руки", то может возникнуть авария. Следовательно, для благоприятного исхода в таких играх у всех игроков должен быть одинаковый подход к выбору правил поведения.

Упражнение 9.3. Объяснить (см. рис. 9.1), почему выигрыши игроков в последнем примере можно задать следующими матрицами:

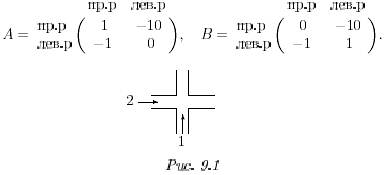
Рассмотренные в примерах 9.2 и 9.3 игры характеризуются следующими соотношениями элементов матриц выигрыша:

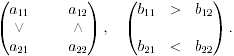
Упражнение 9.4. Проверить, что при выполнении таких соотношений в игре всегда существует два равновесия по Нэшу.

Приведем пример, который показывает, что равновесие по Нэшу может быть неэффективным с точки зрения интересов игроков.

Пример 9.4. Игра "дилемма заключенного":

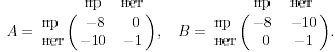
Интерпретация. Два бандита (игроки 1 и 2), подозреваемые в совершении тяжкого преступления, находятся изолированно друг от друга в предварительном заключении. Ввиду отсутствия прямых улик успех или неуспех обвинения зависит от признания (стратегия 1) или непризнания (стратегия 2) самих бандитов. Если оба бандита признаются (ситуация (1,1)), то они будут признаны виновными и приговорены к 8 годам тюрьмы. Если ни один из них не признается (ситуация (2,2)), то по обвинению в главном преступлении они будут оправданы, но обвинителю все-таки удастся доказать их виновность в некотором сопутствующем менее тяжком преступлении, например, в ношении оружия, в результате чего они будут приговорены к 1 году тюрьмы. Если, наконец, признается только один из них (ситуации (2,1) и (1,2)), то признавшийся будет освобожден (за помощь следствию), а непризнавшийся будет приговорен к отбытию максимального срока - 10 лет.

В этой игре имеется единственная ситуация равновесия (1,1): обоим признаться. Однако есть ситуация (2,2), более выгодная обоим игрокам, но не являющаяся ситуацией равновесия. Следовательно, равновесия по Нэшу могут быть неэффективны в том смысле, что за счет отклонения обоих игроков от ситуации равновесия можно улучшить выигрыши каждого из них.

Описанная в примере 9.4 игра имеет следующую структуру:

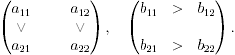
Упражнение 9.5. Проверить, что при выполнении таких соотношений в игре всегда существует единственное равновесие по Нэшу.

В связи с последним примером дадим определение ситуации, оптимальной по Парето.

Определение. Ситуация (x⁰, y⁰) игры Г называется оптимальной по Парето, если не существует такой ситуации (x, y) что выполнены неравенства

F(x, y)  F(x⁰, y⁰), G(x, y)  G(x⁰, y⁰)

и при этом хотя бы одно из них - строгое.

В примере 9.4 в ситуации (2,2) оба игрока получают по -1, что больше, чем их выигрыш -8 в ситуации равновесия (1,1). Следовательно, ситуация равновесия не является оптимальной по Парето.

Упражнение 9.6. Докажите, что в антагонистической игре любая ситуация оптимальна по Парето.

Следующий пример показывает, что не всегда равновесные стратегии являются максиминными.

Пример 9.5. Пусть

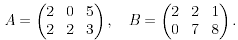
Здесь (1,1) - единственная ситуация равновесия, но стратегия 1 первого игрока не является максиминной. Действительно,

Стратегия 1 второго игрока также не является максиминной. Если игрок неблагожелательно настроен по отношению к партнеру, то он может нарушить соглашение и вместо равновесной стратегии выбрать максиминную. В результате он получит тот же выигрыш 2, что и в ситуации равновесия, а партнер получит 0.

Мы отметили три недостатка понятия равновесия по Нэшу:

1. равновесий по Нэшу в игре может не существовать;

2. равновесие по Нэшу может быть не единственно;

3. равновесие по Нэшу может быть неэффективно.

Но, несмотря на эти недостатки, указанное понятие играет центральную роль в теории принятия решений в конфликтных ситуациях.

Приведем теорему существования ситуации равновесия в игре двух лиц, которая является обобщением теоремы 2.3. Предварительно сформулируем топологическую теорему о неподвижной точке.