4. Свойства решений в смешанных стратегиях
В данном параграфе рассматриваются свойства решений в смешанных стратегиях матричных игр и непрерывных игр на прямоугольнике. Эти свойства в частных случаях позволяют находить оптимальные смешанные стратегии.
Теорема 4.1. Для того чтобы тройка (0, 0, ) была решением в смешанных стратегиях непрерывной игры Г , необходимо и достаточно, чтобы было выполнено условие
(*)
Доказательство.
Необходимость. Пусть (0, 0, ) - решение непрерывной игры в смешанных стратегиях. Тогда = F(0, 0) и по определению седловой точки
Возьмем в последних неравенствах вместо и чистые стратегии x и y. В результате получим условие (*).
Достаточность. Пусть для тройки (0, 0, ) выполнено условие (*). Проинтегрируем первое неравенство этого условия по любой стратегии , а второе - по любой стратегии и получим
Подставляя, в
частности,
= 0
и
= 0,
находим, что F(0,
0)
=
и пара (0,
0)
- седловая точка функции F(,
)
на {}
{}.
Отметим, что теорема 4.1 справедлива для произвольных смешанных расширений антагонистических игр.
Сформулируем аналогичную теорему для матричных игр.
Теорема 4.1’. Для того чтобы тройка (p0, q0, ) была решением в смешанных стратегиях игры с матрицей A, необходимо и достаточно, чтобы было выполнено условие
(*)
Упражнение 4.1. Докажите теорему 4.1’.
Отметим, что проверка выполнения условия (*) теоремы 4.1’ сводится к подсчету скалярных произведений вектора p0 на столбцы, а также вектора q0 на строки матрицы A и сравнению их с числом .
Пример 4.1.
Пусть матрица игры - циклическая:
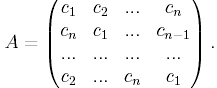
Покажем, что p0
= q0
= (1/n,
..., 1/n),
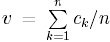- решение игры в смешанных стратегиях.
Действительно, условие (*) здесь выполнено,
поскольку все неравенства в нем выполнены
как равенства. В качестве конкретного
примера рассмотрим игру "мешок,
камень, ножницы"с матрицей
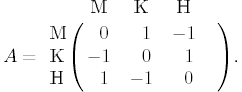
Можно дать следующую интерпретацию этой игры. Двое выбирают один из трех предметов: мешок, камень или ножницы. Каждый предмет против самого себя никакого выигрыша не дает, поэтому на диагонали стоят 0. Ножницы тупятся о камень, поэтому они проигрывают камню 1, а тот в свою очередь выигрывает у ножниц 1. Камень можно поместить в мешок, поэтому мешок выигрывает у камня 1, а камень проигрывает мешку 1. Ножницы режут мешок, поэтому они выигрывают у мешка 1, а мешок проигрывает ножницам 1.
******************
Упражнение 4.2. Пусть B - матрица, полученная прибавлением константы c ко всем элементам матрицы A. Показать, что значения соответствующих матричных игр связаны соотношением (B) = (A) + c, а оптимальные смешанные стратегии игроков совпадают.
Пример 4.2. Продавец выставляет на продажу три предмета, не представляющие для него особой ценности (старые телевизоры и т.п.). Он готов их продать даже за незначительную цену. Имеются два покупателя (игрока), располагающие одинаковыми суммами денег A. Игрок становится обладателем предмета, если предлагает за него сумму, бoльшую, чем партнер. Цель первого игрока состоит в покупке двух каких-либо предметов из трех. Цель второго игрока - воспрепятствовать этому.
Пусть x
= (x1,
x2,
x3)
X
= {x
|
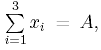xi
= A,
x1,
x2,
x3
0} - стратегия первого игрока, состоящая
в предложении суммы xi
за i-ый
предмет. Аналогичную стратегию
y=(y1,y2,y3)Y=X
использует второй игрок.
Будем писать x
y,
если какие-либо две компоненты вектора
x
больше соответствующих компонент
вектора y.
Определим функцию выигрыша первого
игрока
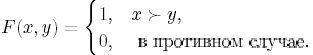
Заметим, что
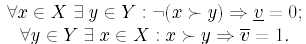
Отсюда следует, что игра не имеет решения в чистых стратегиях. Найдем ее решение в смешанных стратегиях.
Множество стратегий X (совпадающее с Y) изобразим на плоскости в виде равностороннего треугольника высоты A. Точка y имеет барицентрические координаты y1,y2,y3, определяющие ее расстояния от трех сторон треугольника. На рис. 4.1 изображены линии x1 = y1, x2 = y2, x3 = y3.
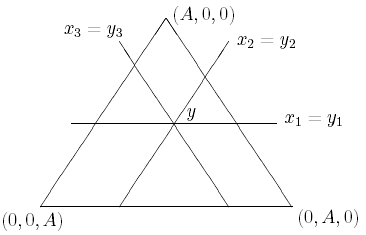
Рис. 4.1
Множество стратегий вне этих линий разобьем на два подмножества
Заметим, что X1(y) является объединением трех треугольников. Например, нижний треугольник на рис. 4.1 состоит из таких векторов x, для которых x2 > y2, x3 > y3.
Множество
представляет собой правильный шестиугольник с центром y0, совпадающим с центром треугольника X (рис. 4.2).
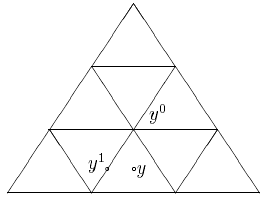
Рис. 4.2
Пусть 0 - равномерное распределение на C. Докажем, что тройка