Министерство образования Российской Федерации

Уральский Государственный Технический Университет

Кафедра “Автоматика и информационные технологии”

Курсовая работа

Вычислительная программа для сравнительного анализа работы

среднеквадратического и минимаксного метода оценивания

неизвестного параметра.

по дисциплине «Математические основы теории систем и сигналов»

Вариант №2

ВЫПОЛНИЛ:

ПРОВЕРИЛ: Кумков С.И.

Екатеринбург 2003 г.

Содержание

1. Задание………………..…………………………………….. .3

2. Постановка задачи……………..…………………………….4

3. Моделирующая программа……………..…………………...6

3.1. Последовательность вычислений………………………..….6

3.2. Блок-схема программы………………………………………8

4. Результаты моделирования……………………...……….....10

5. Приложение 1. Текст моделирующей программы…….….11

6. Список литературы………………………………………….13

Задание

Замеры неизвестной константы С_ист производятся с ошибкой Е имеющей равномерное распределение плотности вероятностей из интервала [-E_max, E_max], где E_max - максимальная величина ошибки (по модулю).

Стандартный метод обработки набора замеров {Х_i , i=1,N} заключается в нахождении усредненной оценки С_ср в соответствии с методом минимума среднеквадратического отклонения.

Минимаксное оценивание неизвестной величины заключается в определении интервала допустимых значений неизвестной величины, совместных с полученным набором замеров. Данный интервал находится как логическое произведение-пересечение интервалов неопределенности {Н_i , i=1,N} замеров {Х_i}. Причем интервал неопределенности для каждого замера строится

Н_i = [F_H (i) = Х_i - E_max , F_В (i) = Х_i + E_max]

, где F_H (i), F_В (i) – нижняя и верхняя границы интервала неопределенности.

Интервал I допустимых значений неизвестной величины имеет вид I=[I_H,I_B], где I_H, I_B – нижняя и верхняя границы. Данный интервал играет роль доверительного, а в случае необходимости его центр выдается потребителям в качестве точечной оценки неизвестной оцениваемой константы С_minmax = (I_H +I_B)/2.

Разработать алгоритмы и программу , реализующую: а) формирование массива зашумленных входных замеров; б) расчет оценки С_ср по стандартному методу; в) расчет интервала неопределенности I и оценки С_minmax ; г) определение вероятностей попадания оценки С_ср и С_minmax в заданный интервал +-5% относительно истинного значения (вероятности находятся методом статического моделирования).

ОТЧЕТ по работе должен содержать:

1. Постановку задачи: описание метод решения, выбранных алгоритмов расчетных формул, метода получения входной информации.

2. Описание последовательности вычислений и блок-схему программы.

3. Текст отлаженной программы с комментариями основных блоков.

4. Результаты отладки и контрольного расчета по разработанной программе, визуализацию и пояснение работы входных и выходных результатов каждого метода, получение оценки вероятностей.

2. Постановка задачи

Вычислительный комплекс производит замеры некоторой неизвестной константы С_ист. Замеры зашумлены и производятся с ошибками. Ошибки являются случайными величинами с равномерным распределением на заданном интервале:[ - E_max, E_max ] , значит измеренные значения X_i {i=1,N} константы С_ист также являются случайными величинами и в каждом замере X_i могут принимать одно из значений на интервалах [(С_ист – E_max), (С_ист + E_max)] – для всех замеров.

Покажем это наглядно на рис.1.

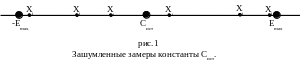
Для получения измеренных значений константы С_ист необходимо смоделировать ошибки замеров. В модели вычислительной системы, ошибки замеров будут формироваться с помощью функции Random [(Range:Word)] языка программирования Turbo Pascal 7.0 [2]. Эта функция возвращает случайное число в пределах диапазона значений, на который указывает параметр Range. Получаем модель замера X_i константы С_ист:

X_i = С_ист + 2* Е_max*(Random (1)-0.5) (1)

Создавая цикл получения X_i в пределах от 1 до N, получим набор замеров совместный с заданными условиями.

Стандартный метод обработки замеров X_i заключается в нахождении усредненной оценки С_ср в соответствии с методом минимума среднеквадратического отклонения. В соответствии с методом наилучшее математическое ожидание С_ср искомой константы С_ист вычисляется как среднее арифметическое всего набора замеров X_i [1], т.е.

(2)

При этом величина ошибки С_срerr вычисляется как среднеквадратическое отклонение [1] по формуле:

(3)

Полученная таким образом оценка С_ср искомой константы С_ист будет заключаться в интервале [С_срн=(С_ср - С_срerr), С_срв=(С_ср + С_срerr)].

Рассмотрим минимаксное оценивание измеряемой постоянной величины, заключающееся в определении интервала I допустимых значений константы, совместного с полученным набором замеров. Данный интервал I находится как логическое произведение-пересечение интервалов неопределенности {Н_i , i=1,N} замеров {Х_i}. Причем интервал неопределенности для каждого замера строится

Н_i = [F_H (i) = Х_i - E_max , F_В (i) = Х_i + E_max] (4)

, где F_H (i), F_В (i) – нижняя и верхняя границы интервала неопределенности Н_i для отдельного замера Х_i.

Интервал I допустимых значений неизвестной константы имеет вид I=[I_H,I_B], где I_H, I_B – нижняя и верхняя границы. Данный интервал играет роль доверительного, а в случае необходимости его центр выдается потребителям в качестве точечной оценки неизвестной оцениваемой константы С_minmax = (I_H +I_B)/2. Поясним это графически:

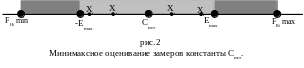
Проанализировав вышеперечисленное, можно сделать вывод, что значения верхней I_B и нижней I_H границы допустимых значений константы С_ист лежат в диапазоне от F_Hi min до F_Bi max который в 2 раза больше соответственного диапазона для стандартного метода. Вместе с тем, так как в этом методе используется логическое пересечение-произведение интервалов неопределенности для каждого замера, то у его точность должна быть не намного хуже стандартного метода. Для реализации минимаксного метода необходимо получить два массива данных, один для F_Hi , другой для F_Bi соответственно, тогда алгоритм построения произведения-пересечения будет оптимально производительным: верхняя граница допустимых значений I_B константы С_ист будет равна минимальному значению F_Bi, а нижняя граница допустимых значений I_H константы С_ист будет равна максимальному значению F_Hi. Необходимо также проверить вероятность того, что I_H = I_B , что означает точное попадание C_minmax = I_H = I_B = С_ист.

Определение вероятностей попадания полученных вышеперечисленными способами оценок С_ср и C_minmax в заданный интервал +-5% относительно истинного значения С_ист проводится методом статистического моделирования. Для равномерного распределения справедливо [1], что плотность вероятности f(x) на всем заданном интервале [a,b] постоянна, а вне интервала равна 0. Таким образом, вероятность f(x) обнаружения истинного значения случайной величины на заданном интервале [a,b] равна [1, стр. 786] следующему выражению:

(5)

Согласно классическому определению вероятности события Р(х) [1]:

(6)

Благоприятными событиями для попадания оценок С_ср и C_minmax в заданный интервал +-5% относительно истинного значения С_ист является попадание их доверительных интервалов в 5% допуск. Иначе говоря, чем большая часть доверительного интервала попадает в заданный допуск, тем больше вероятность обнаружить полученные оценки С_ср и C_minmax в заданном диапазоне ошибок. Или графически:

Следует отметить, что такой вывод сделан на том основании, что мы имеем дело с равномерным распределением, а не с более сложными видами распределения, в другом случае пришлось бы использовать более сложные математические аппараты (интегрирование и определение доверительной вероятности по специальным таблицам) для определения вероятности.