Билет №1

1.Оптимизационные задачи.

Задачей оптимизации в математике, информатике и исследовании операций называется задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Постановка задачи оптимизации

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией. Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ^* , который доставляет минимальное значение f(χ^*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество — множество

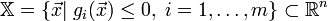
2. Целевую функцию — отображение ;

3. Критерий поиска (max или min).

Тогда решить задачу означает одно из:

1. Показать, что .

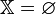2. Показать, что целевая функция не ограничена снизу.

3. Найти .

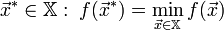4. Если , то найти .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек таких, что всюду в некоторой их окрестности для минимума и для максимума.. Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизаци.

Исслед-е опер-ций – комплексн. мат.дисциплина, заним-ся построением, анализом и применением мат.моделей принятия оптим-х реш-й при провед-и операций.

Операция-это сис-ма управл-х д-ий, объед-ные единым замыслом и напрвл-ные на достижение опред.цели.

Лин-е програм-е (ЛП).Общая задача ЛП состоит в нахождении экстремума (макс.или минимума)линейной целевой ф-ции.

Вектор х=(х1,х2,…,хn), удовл-щий с-ме1, назыв.допустимым решением или планом задачи ЛП (ЗЛП).

Мн-во всех планов назыв. допустимой обл. или обл. допустимых реш-й.

План, к-рый доставл-т макс-м (мин) целевой ф-ции назыв. оптимальным планом или оптим-м реш-ем ЗЛП. Общая задача ЛП м.б.приведена к единому стандарт-му виду, в к-ром целевая ф-ция д.б. максимизирована, а все ограничения д.б. записаны в виде равенств с неотриц-ми переменными.

Стандарт-я форма назыв. осн.задачей ЛП (ОЗЛП). Привести общую задачу ЛП к осн. очень просто:

1)минимизация целевой ф-ции f равносильна максимизации целевой ф-ции g=f.

2)ограничения в виде нерав-в

это равносильно ур-ю

при условии, что доп.переменная

. А нерав-во вида

равносильно сис-ме

3)если на нек-рую переменную 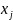не накладыв-ся условия неотриц-сти, то делают замену

Геометрический метод

м.б. применен, если модель содержит только 2перем-е. В случае 3х перем-х этот метод становится менее наглядным, а при большем числе перем-х невозможным.

Пример: предприятие изготавл-т 2вида краски(1и2). Для их произв-ва исп-ся 2исходн.продукта (АиВ). Расходы исходн.продуктов и максим-е суточные запасы указаны в таблице

Исх. продукт	Расход исх.прод-в на 1тонну краски		Суточн. запас, т
	1	2
А	1	2	6
В	2	1	8

Изучение рынка сбыта показало, что суточн.спрос на 2краску не превышает спроса на 1ю краску более чем на 1 тонну. Кроме того, установлено, что спрос на 2ю краску никогда не превыш-т 2 тонны в сутки. Цены на 1т красок равны 3у.е. для 1й краски, 2у.е. для 2й краски.Какое кол-во краски кажд.вида д-но произв-ть предприятие, чтобы доход от реализации продуктов был максим-м.

Решение: х1,х2 – кол-во 1и2краски в тоннах, проивед-х предприятием.

Целевая ф-ция

при ограничениях

Изобразим на координ-й плоскости обл.допустимых решений. Мн-во решений кажд.из нерав-в есть полуплоскость, на к-рую указыв-т стрелка. Граница полуплоскости (прямая) задается соотв-щим ур-м (когда знак нерав-ва замен-ся знаком рав-ва).

Полученная т.о. допустимая обл. –многогранник OABCDE. Необх-мо среди точек этого многогранника найти точку, в к-рой целевая ф-ция f принимает макс-е знач-е. Рассм-м так называемую линию уровня ф-ции f, т.е. линию, вдоль к-рой эта ф-ция принимает одно и тоже фиксированное знач-е c

В данном случае линия уровня – это прямая. При разл. С –линии уровня параллельны.

Точка В есть точка пересечения прямых (1) и (2).

Симплекс-метод(СМ)

Наиболее популярным универс-м алгебраич-м методом реш-я ЗЛП явл. СМ, разработанный амер. Ученым Дж.Данцигом в 1949году.

Сис-ма линейных ур-й назыв. сис-мой с базисом, если в кажд.ур-и содер-ся неизв-е с коэф-ом =1, отсутствующее в ост.ур-ях сис-м. Эти неизв-е назыв. базисными, ост-е свободными

Данная сис-ма всегда имеет решение:

к-рое назыв. базисным решением. Сис-ма линейных ур-й назыв. канонической , если она явл. сис-мой с базисом и все >= 0. Базисное решение в этом случае явл. планом, т.к. его компоненты неотриц-ны. Назовем его базисным или опорным планом канонич.с-мы. Осн. ЗЛП будем назыв. канонич-й (КЗЛП), если сис-ма лин.ур-й этой задачи канонич-я, а целевая ф-ция выражена только ч/з своб.перем-е. Решение КЗЛП симплекс-методом удобно записывать в виде симплекс таблиц(СТ). СТ предст.собой матрицу коэф-ов какнонич.сис-мы ур-й и коэ-ов при неизв-х в целевой ф-ции, а также указанием базисных неизв-х.

Рассм-м КЗЛП, состоящую в максимизации целевой ф-ции вида:

на мн-ве планов канонич.сис-мы.

Симплекс-таблица

Базис	х1 х2 …	Знач-е

Посл.строка СТ назыв. индексной. Она соотв-т ур-ю:

Алгоритм СМ:

1.Записыв-м данную КЗЛП в исходную СТ.

2. Если все эл-ты индексной строки СТ неотриц-ны, то базисный план задчи явл. оптимальным.

3.Если в индексной строке содер-ся отриц.эл-т, над к-рым в табл. Нет ниодного положит-го, то целевая ф-ция неограничена сверху на мн-ве планов и задача не имеет решений.

4. Если над каждым отриц-м эл-ом индексной строки имеется в табл.хотя бы 1положит-й, то следует перейти к новой СТ, д/к-рой базисный план не хуже предыдущего. С этой целью:

А)выбираем в таблице ключевой столбец, в основании к-рого наход-ся к-либо отриц-й эл-т индексной строки;

Б) выделяем ключевое отн-ние (мин-е из отн-ний к полож-м эл-м ключевого столбца), знаменатель к-рого будет ключ.эл-ом;

В) составляем новую СТ. Д/этого делим ключ.строку (строка, в к-рой наход-ся ключевой эл-т) на ключ.эл-т, а затем из всех остальных строк, включая индексную вычитаем полученную строку, умноженную на соотв-щий эл-т ключевого столбца (чтобы все эл-ты этого столбца, кроме ключевого стали равны 0)

5. При рассм-нии СТ непременно представится один из трех случаев, описанных в пунктах 2,3,4.

Если при этом возникнут ситуации 2или 3, то процесс решения задачи заверш-ся.

Если же возникнет ситуация пугкта 4, то процесс продолж-ся.

Замечание: в качестве ключевого столбца выбир-ся тот, к-рый отвеч-т наибольшему по модулю отриц-му эл-ту индексной строки.

Двойственные задачи

Рассм-м задачи об испол-и сырья.

Пусть имеется m видов сырья, запасы к-рых равны b1, b2,…,bm.Из этого сырья произв-т n видов продукции. Расходы сырья iтого вида на произв-во единицы продукции jго вида равны . Прибыль от продажи единицы продукции jго вида равна 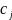. Найти такой план выпуска продукции, чтобы суммарная прибыль была максимальна. Матем.модель этой задачи имеет вид

Х1, х2,…, хn – кол-во единиц продукции соответствующего вида.

Задача 2.

Поставим целью назначить справедл-е продажные цены на все имеющиеся виды сырья и пусть – цена единицы сырья i-того вида. Потребуем, чтобы продажная цена сырья необх-го д/произв-ва продукции опред.вида была не меньше выручки, к-рую можно получить при реализации этой продукции.

Рассм-м задачу минимизации стоим-сти всего сырья.

Матем.модель:

Эти задачи явл.симметричными двойственными задачами.

Особенности этих задач:

1.Одна задача явл. задачей максимизации, др. –минимизации.

2. В задачи максимизации все нерав-ва (≤), а в задачи минимизации - ≥

3. Число неизв-х одной задачи равно числу нерав-в другой.

4. Матрицы кооэф-ов при неизв-х в нерав-вах обеих задач явл. взаимнотранспонированными.

5. Свободные члены нерав-в одной из задач равны кооэф-м соотвующих неизвестных в выражении целевой ф-ции др.задачи.

Теорема 1.

Знач-е целевой ф-ции задачи максимизации д/любого ее плана не превосходит знач-я целевой ф-ции двойственной ей задачи минимизации д/любого ее плана, т.е. f(x)≤g(y) называемое осн. нерав-ом двойственности.

Осн. теорема двойственности.

Если задача ЛП имеет конечный оптимум, то двойственная к ней также имеет конечный оптимум и оптимальные знач-я целевых ф-ций совпадают.

Если целевая ф-ция одной из двойств-х задач не ограничена, то условия др.задачи противоречивы.

Теорема о дополняющей нежесткости

Для того, чтобы допустимое решение

Двойств-х задач явл-сь оптимальными необх-мо и достат-но, чтобы выполн-сь след.соотн-ния: