4.2 Перевірка стійкості системи за критерієм Ляпунова

Критерій Ляпунова дає можливість зробити висновок про стійкість системи на основі аналізу коренів її характеристичного рівняння на основі положень «Теореми Ляпунова».

Теорема Ляпунова: Для стійкості лінійної САК необхідно, щоб усі корені характеристичного рівняння системи мали від’ємні дійсні частини. Якщо хоча б один корінь характеристичного рівняння має додатню дійсну частину, то система є нестійкою.

У випадку, якщо характеристичне рівняння має хоча б один нульовий корінь, або пару уявних коренів, то така система знаходиться на межі стійкості.

Розглянемо характеристичне рівняння досліджуваної сак:

(4.9)

визначимо дискримінант:

(4.10)

Запишемо формули для знаходження коренів рівняння:

(4.11)

(4.12)

Оскільки система має чисто уявні корені, тому її можна вважати такою, що знаходиться на межі стійкості.

4.3 Перевірка стійкості замкнутої системи за критерієм Гурвіца.

Критерій Гурвіца дозволяє визначити стійкість замкненої системи по коефіцієнтам характеристичного рівняння.

Для отримання коефіцієнтів матриці знайдемо і розв’яжемо характеристичне рівняння:

(4.13)

(4.14)

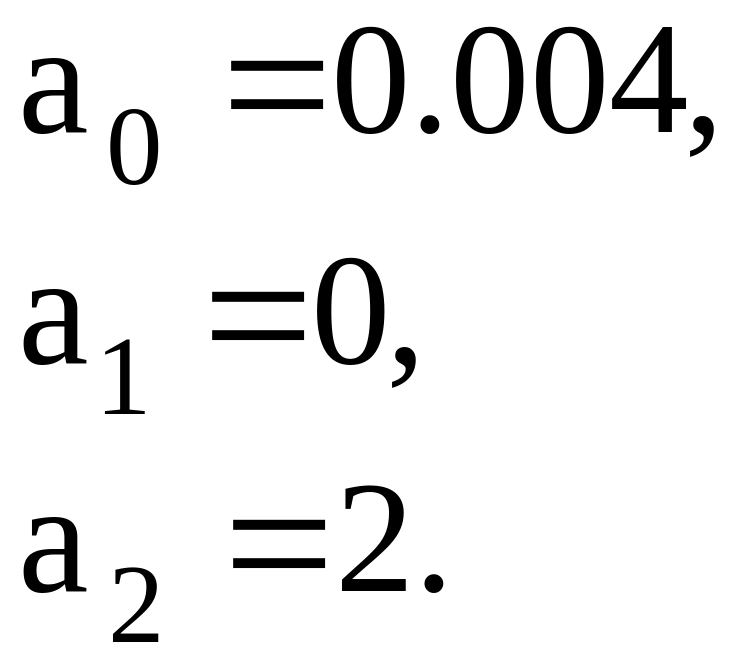
Для даного характеристичного рівняння складаємо квадратну матрицю в такому порядку: по головній діагоналі матриці виписуємо всі коефіцієнти від до ; відносно кожного елементу діагоналі донизу записуємо коефіцієнти при старших похідних; відносно кожного елементу діагоналі доверху записуємо коефіцієнти при молодших похідних.

(4.15)

Де а0, а1, а2 – коефіцієнти характеристичного рівняння.

(4.16)

За критерієм Гурвіца система знаходиться на межі стійкості оскільки із формули (4.14)

а₀=0,004, (4.17)

визначники Гурвіца дорівнюють нулю:

(4.18)

(4.19)

То можна зробити висновок,що а₀>0,то система знаходиться на межі стійкості.

4.4 Перевірка стійкості розімкнутої системи за критерієм Михайлова.

Даний критерій дає можливість судити про стійкість системи по її частотним характеристикам. Згідно критерію для стійкості системи необхідно і достатньо, щоб годограф Михайлова при зміні частоти від 0 до починав свій рух з точки, розташованої на дійсній додатній напівосі комплексної площини, обертався проти годинникової стрілки, ніде не переходив в нуль і послідовно обійшов всі n-чверті комплексної площини.

Для перевірки стійкості за критерієм Михайлова проведемо наступні дії:

(4.11)

(4.12)

Виділимо дійсну частину рівняння

(4.13)

та уявну частину рівняння :

(4.14)

Побудуємо годограф Михайлова (рисунок 4.2), для чого у вирази для знаходження дійсної та уявної частини підставимо значення діапазону частоти . Значення розрахованих точок представлене в таблиці 4.2

Таблиця 4.2 – Розрахункові точки для побудови годографа Михайлова

	0	5	10	15	20	50
	2	1.9	1.6	1.1	0.4	-8
	0	0	0	0	0	0

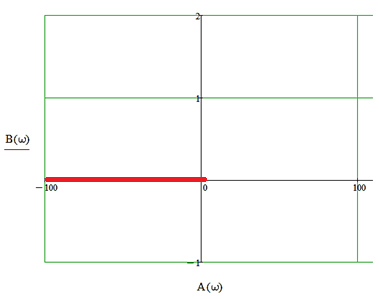
Рисунок 4.2 – Годограф Михайлова для розімкнутої системи

З рисунку 4.2 можна зробити висновок, що система знаходиться на межі стійкості, оскільки описується, рівняння першого порядку і годограф проходить по вісі абсцис у від’ємному напрямку через нульову точку площини.

5 ВИЗНАЧЕННЯ ПРЯМИХ ПОКАЗНИКІВ ЯКОСТІ ТА КОРЕКЦІЯ ЗАМКНУТОЇ СИТЕМИ

Для визначення прямих показників якості замкненої системи попередньо позначимо їх на графіку перехідної характеристики системи (рисунок 5.1).

До прямих показників якості відносять такі:

Н_min.– мінімальне значення перехідного процесу.

Н_max– максимальне значення перехідного процесу.

n – кількість піків.

f – частота.

σ – перерегулювання.

t_р – час регулювання.

t_у – час встановлення.

Рисунок 5.1–Графік перехідного процесу замкнутої системи

Типових показників якості немає, оскільки система знаходиться на межі стійкості. Але знайти деякі показники все-таки можна.

Мінімальне значення Н_min.=0,

Максимальне значення Н_max.=100,

Кількість коливань n=3. при

Частота дорівнює:

                              (5.1)

Для корекції даної системи використаємо від’ємний зворотний звязок із передаточною функцією виду:                                                         

   (5.2)

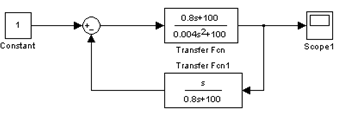
Рисунок 5.2 – Замкнена система побудована у ППП Mathlab

_{Після математичних дій, ми отримаєм вираз:}                                                     (5.3)

_{Структурна схема досліджуваної системи представлена на рисунку 5.3.}

Рисунок 5.3 – Відкорегована замкнена система побудована у ППП Mathlab

Перехідний процесс відкорегованої ситеми показаний на рисунку 5.4.

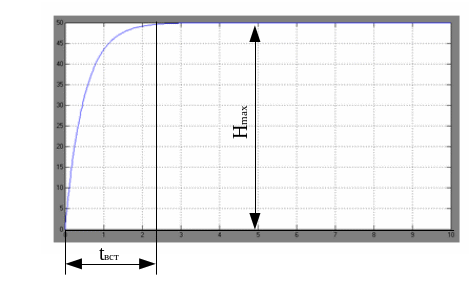
Рисунок 5.4 – Перехідний процесс відкорегованої замкненої системи

Мінімальне значення Н_min.=0,

Максимальне значення Н_max.=50,

Час встановлення

6 ЗАПАСИ СТІЙКОСТІ ЗАМКНУТОЇ СИСТЕМИ ЗА АМПЛІТУДОЮ І ЗА ФАЗОЮ

Запасом по модулю називається величина в децибелах, на яку потрібно змінити коефіцієнт перетворення САК, щоб приведена система опинилася на межі стійкості.

Для визначення запасу стійкості здійснимо побудову логарифмічних характеристик, які зображені на рисунку 6.1.

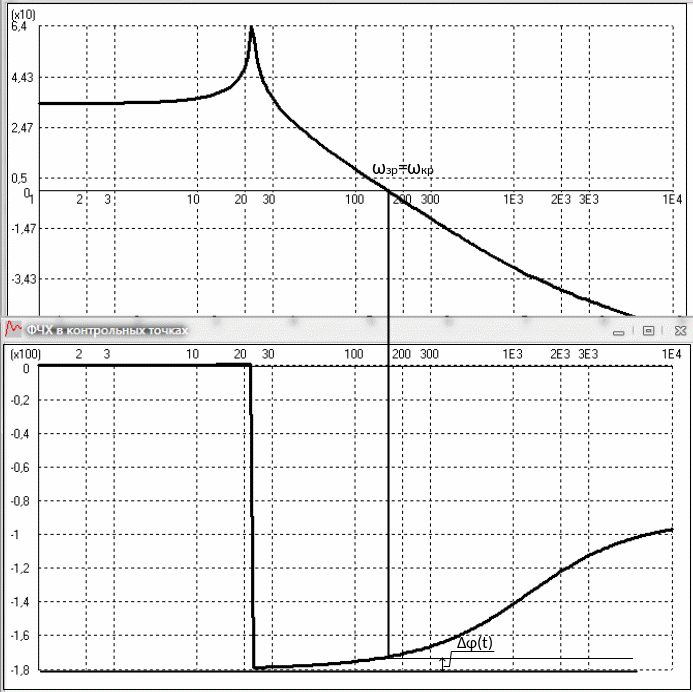
Рисунок 6.1–Графік для визначення запасу стійкості системи за амплітудою і фазою

Запасом стійкості за фазою називається кут, на який потрібно повернути амплітудно-фазову характеристику розімкненої системи, щоб замкнута САК опинилася на межі стійкості.

Визначимо запас стійкості по фазі. Для цього скористаємось наступною формулою:

(6.1)

підставивши значення отримуємо значення запасу стійкості по фазі:

(6.2)

Запас стійкості по амплітуді визначається по критичній частоті, коли фаза дорівнює -180:

(6.3)

Але оскільки крива ЛФЧХ не перетинає вісь –π(-180), а лише досягає її рівня,то можна зробити висновок що система не має запасу стійкості по амплітуді оскільки відсутня .