ВСТУП
Теорія автоматичного керування (ТАК) вивчає принципи побудови систем автоматичного керування і закономірності процесів, що в них протікають, які вона досліджує на динамічних моделях реальних систем з урахуванням умов роботи, конкретного призначення та конструктивних особливостей керування об'єкта і автоматичних пристроїв, з метою побудови працездатних і точних систем керування.
Керування будь-яким об’єктом, це виконання відносно нього дій, для того щоб досягнути потрібного стану або процесу. В якості об’єкта керування може бути літак, станок, електродвигун і т.п. Управління об’єктом з допомогою технічних засобів без участі людини називається автоматичним управлінням. сукупність об’єктів керування і засобів автоматичного управління називають системою автоматичного керування.
Системи автоматичного керування – це сукупність об’єкта керування (машина, механізм) та з’єднаних певним чином елементів, взаємодія яких забезпечує розв’язання певного завдання керування об’єктом.
Теорію керування замкнутих систем називають теорію автоматичного регулювання (ТАР). Під регулювання розуміють підтримання заданих значень регульованої величини на певному рівні.
Завданням даної курсової роботи є дослідження аналітичним шляхом частотних характеристик, побудова вагової та перехідної характеристик, перевірки стійкості системи за критеріями Гурвіца та Михайлова, визначення запасів стійкості за амплітудою та за фазою і виконання комп’ютерного моделювання – для закріплення теоретичних знань з дисципліни «Теорія автоматичного керування».
1 ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ЕЛЕМЕНТІВ ЧОТИРЬОХПОЛЮСНИКА
Для побудови та математичного запису диференціальних рівнянь окремих елементів чотириполюсника та диференціального рівняння, що зв’язує вхідну та вихідну напруги чотириполюсника, спершу запишемо вхідні дані кожного елемента даного чотириполюсника.
Вхідні дані елементів даної схеми:
(Ом),
(Ом),
(мГн).
Для лінійного чотириполюсника рівняння окремих елементів матимуть вигляд: для першого та другого активних опорів:
(1.1)
де
–
напруга на резисторі
;
– струм,
який протікає через елемент.
Напруга
на резисторі
визначається:
(1.2)
де
– напруга на резисторі
;
відповідно, для індуктивності :
(1.3)
Позначимо контурні струми, які протікають в даному чотириполюснику. Схема чотирьохполюсника із вказаними вище позначеннями приведена на рисунку 1.1.
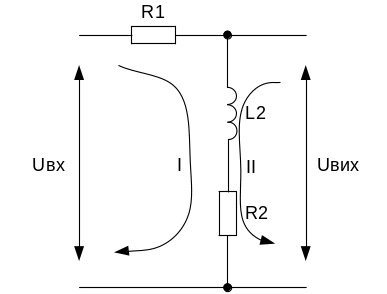
Рисунок 1.1 – Схема чотириполюсника
Запишемо рівняння вихідної та вхідної напруг:
(1.4)
(1.5)
де
,
– значення вхідної та вихідної напруги
чотириполюсника відповідно.
2 ПЕРЕДАТОЧНА ФУНКЦІЯ РОЗІМКНУТОЇ СИСТЕМИ
Перетворимо отримані в розділі 1 рівняння відносно комплексної змінної «р». Для цього використовуємо рівняння прямого перетворення Лапласа:
. (2.1)
В результаті прямого перетворення Лапласа,отримаємо:
(2.2)
(2.3)
За отриманими виразами, використовуючи відоме визначення, можна знайти вираз передаточної функції розімкнутої системи (чотириполюсника).
Передаточна функція чотириполюсника – це відношення зображень вихідної напруги до вхідної. Таким чином отримаємо передаточну функцію даного чотириполюсника:
, (2.4)
. (2.5)
Підставимо значення елементів чотириполюсника в рівняння (2.5). Передаточна функція чотириполюсника набуде вигляду:
. (2.6)
3 ВИВЕДЕННЯ ТА ПОБУДОВА ГРАФІКІВ ДИНАМІЧНИХ ХАРАКТЕРИСТИК СИСТЕМИ
3.1 Передаточна функція замкненої системи
Структурна схема системи, охопленої зворотним зв’язком, представлена на рисунку 3.1.
Рисунок 3.1 – Структурна схема системи охопленої зворотнім зв’язком
Передаточна функція послідовного з’єднання матиме вигляд:
(3.1)
Знайдемо
передаточну функцію розімкнутої системи,
згорнувши дві паралельно розташовані
ланки
та
:
(3.2)
Для виконання подальших досліджень спершу отримаємо передаточну функцію замкнутої системи шляхом послідовного згортання вище приведеної структурної схеми.
Передаточна функція системи, охопленої зворотнім зв’язком, буде мати вигляд:
(3.3)
Передаточна функція в каналі зворотного зв’язку має вигляд:
(3.4)
Підставивши наведені в завданні значення в рівняння замкнутої системи, отримаємо передаточну функцію виду:
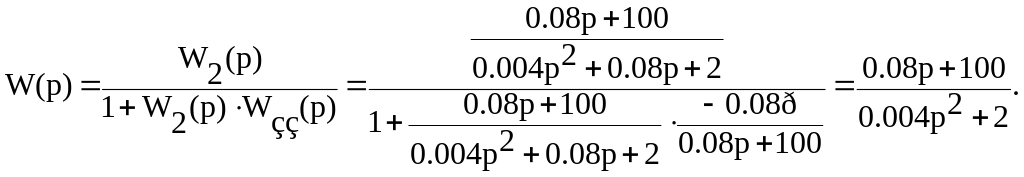(3.5)
Загальна передаточна функція системи охопленої зворотнім зв’язком матиме вигляд:
(3.6)
3.2 Частотні характеристики замкненої системи
Для отримання передаточної функції W(w), використовуючи ППП Mathcad, проведемо такі дії:
Для переходу до частотних характеристик в ППП Mathcad введемо заміну виду:
(3.7)
яка позначає відому математичну рівність виду:
(3.8)
Рівняння АФЧХ знаходимо за допомогою функції «substitute», синтаксис запису в ППП Mathcad має вигляд:
(3.9)
Тоді кінцевий вираз АФЧХ системи матиме вигляд:
(3.10)
Для виділення дійсної Р(w) і уявної Q(w) частини передаточної функції W(w) виконаємо такі дії:
Рівняння АФЧХ знаходимо за допомогою функції «complex», синтаксис запису в ППП Mathcad має вигляд:
(3.11)
отримаємо результат:
(3.12)
З отриманого виразу виділимо дійсну частину:
(3.13)
Уявна частина матиме вигляд:
(3.14)
Відповідно до формули (3.13) графік дійсної частотної характеристики(ДЧХ) матиме вигляд приведений на рисунку 3.1.
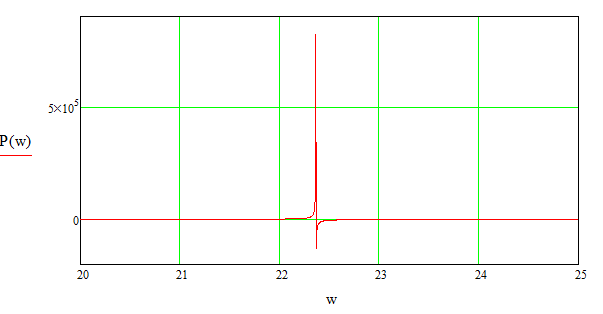
Рисунок 3.1 – Графік ДЧХ системи
Відповідно до формули (3.14) графік уявної частотної характеристики (УЧХ) матиме вигляд приведений на рисунку 3.2.
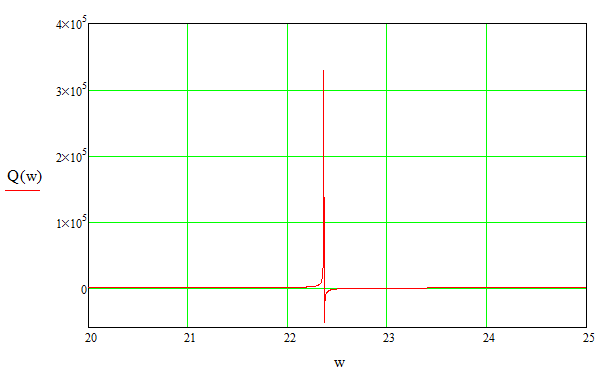
Рисунок 3.2 – Графік УЧХ системи
Для отримання амплітудо-частотної
характеристики (АЧХ)
використовуємо функцію «simplify»,
синтаксис запису в ППП Mathcad
має вигляд:
(3.15)
Тоді кінцевий вигляд рівняння АЧХ буде системи матиме вигляд:
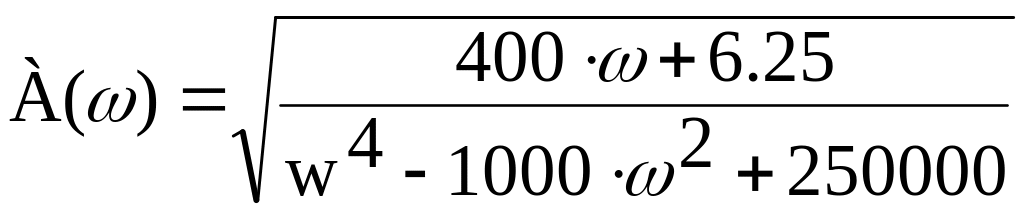(3.16)
Згідно формули (3.16) графік АЧХ матиме вигляд приведений на
рисунку 3.3.
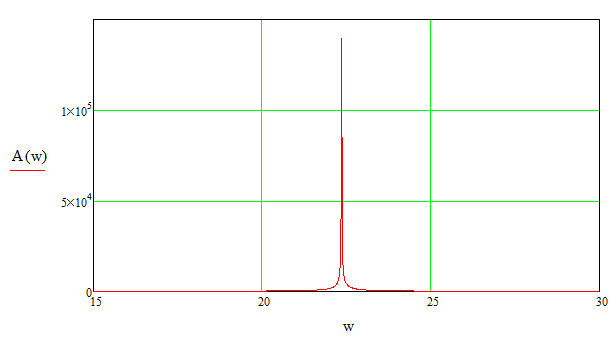
Рисунок 3.3 – Графік АЧХ системи
Для отримання фазо-частотної характеристики
(ФЧХ)
використовуємо функцію «simplify»,
синтаксис запису в ППП Mathcad
має вигляд:
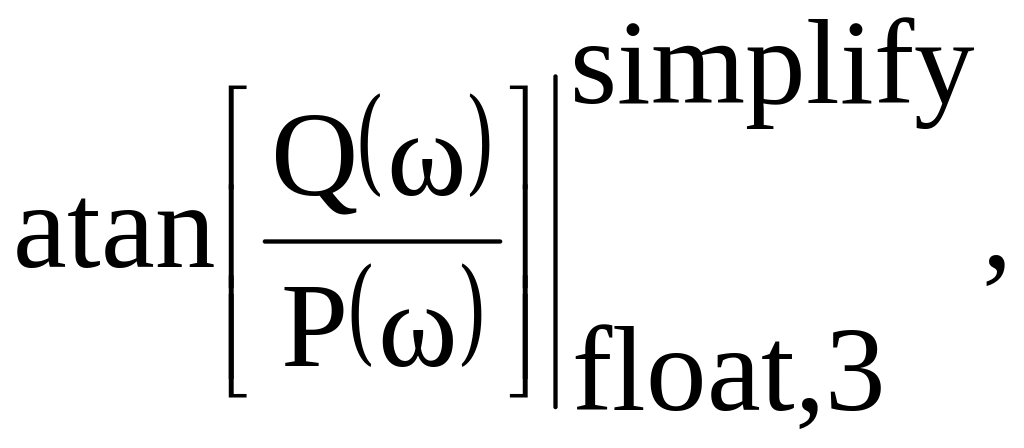(3.17)
(3.18)
Згідно формули (3.18) графік ФЧХ матиме вигляд приведений на
рисунку 3.4.
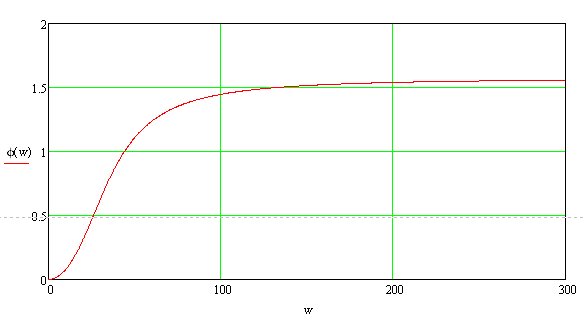
Рисунок 3.4 – Графік ФЧХ системи
Графік логарифмічної фазно-частотної характеристики (ЛФЧХ) матиме вигляд приведений на рисунку 3.5.
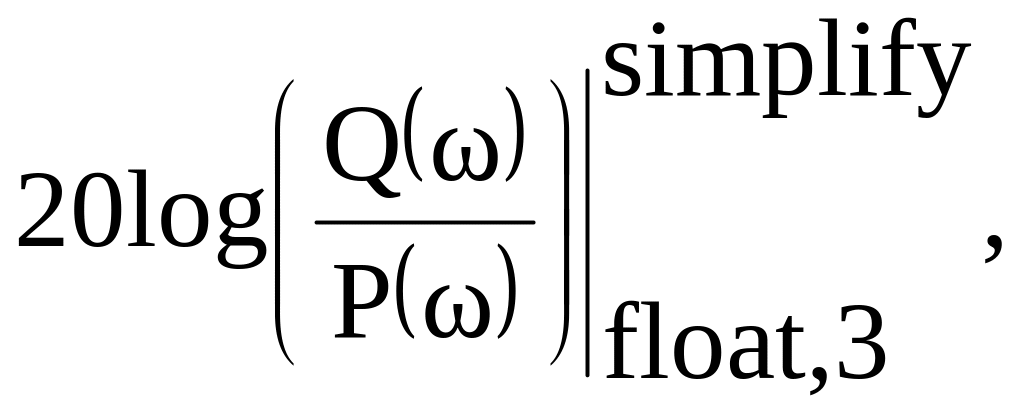(3.19)
(3.20)
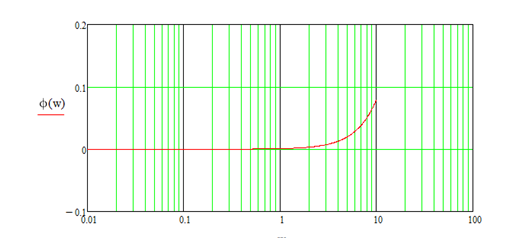
Рисунок 3.5 – Графік ЛФЧХ системи
Для отримання логарифмічної
амплітудо-частотної характеристики
(ЛАЧХ)
використовуємо функцію «simplify»,
синтаксис запису в
ППП Mathcad має вигляд:
(3.21)
(3.22)
Згідно формули (3.20) графік ЛАЧХ матиме вигляд приведений на рисунку 3.6.
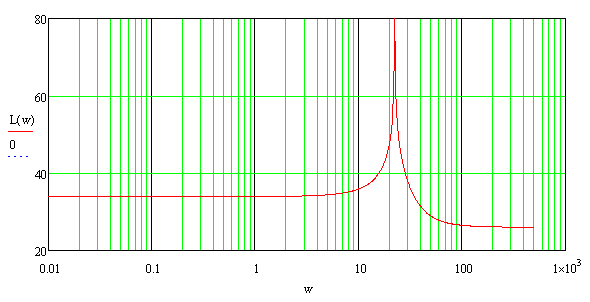
Рисунок 3.6 – Графік ЛАЧХ системи
Побудуємо графік АФЧХ матиме вигляд приведений на рисунку 3.7.
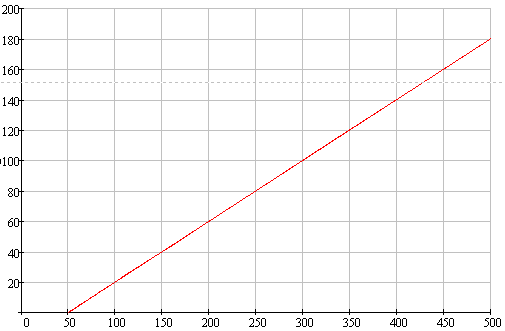
Рисунок 3.7 – Графік АФЧХ системи
3.3 Перехідна характеристика замкненої системи
Перехідної характеристики h(t) має вигляд :
(3.23)
Для отримання перехідної характеристики h(t) використовуємо функцію «invlaplase», синтаксис запису в ППП Mathcad має вигляд:
(3.24)
Після перетворень,кінцевий вираз має вигляд:
(3.25)
Згідно формули (3.23) графік перехідної характеристики матиме вигляд приведений на рисунку 3.8.
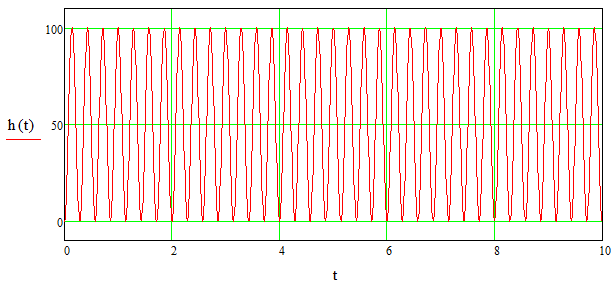
Рисунок 3.8 – Графік перехідної характеристики
Для перевірки правильності виконання побудови перехідної характеристики в ППП Mathcad проведемо розрахунок за Теоремою розкладу та побудуємо графік перехідної характеристики з отриманого результату.
Рівняння перехідної характеристики відносно зображень має вигляд:
(3.26)
(3.27)
Визначимо корені характеристичного рівняння:
(3.28)
(3.29)
Знаходимо дискримінант квадратичного рівняння:
(3.30)
Знайдемо значення поліномів характеристичного рівняння.
поліном чисельника:
(3.31)
(3.32)
(3.33)
поліноми знаменника:
(3.35)
Відштовхуючись від результатів попередніх розрахунків можемо знайти значення перехідної характеристики за теоремою розкладу. Для цього використаємо формулу:
(3.39)
(3.40)
(3.41)