4. Виды денежных потоков

Мы рассмотрели единичные платежи. Однако на практике гораздо чаще при­ходится иметь дело с их совокупностями, а потому одним из основных элементов методик финансового анализа является оценка денежного потока CF_l> CF₂,.... CF„, генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования того или иного вида активов. Эле­менты потока {CF*} могут быть либо независимыми, либо связанными опреде­ленным алгоритмом. Временные периоды чаще всего предполагаются равными. Хотя данное условие, в принципе, не является обязательным, в дальнейшем мы будем придерживаться его. Кроме того, для простоты изложения материала предполагается, что элементы денежного потока являются однонаправленными, т. е. нет чередования оттоков и притоков денежных средств. Также считается, что генерируемые в рамках одного временного периода поступления имеют место либо в его начале, либо в его конце, т. е. они не распределены внутри периода, а сконцентрированы на одной из его границ. В первом случае поток называется потоком цренумерандо, или авансовым, во втором — потоком постнумерандо (рис. 6.7).

г

Рис. 6.7. Графическое представление потоков постнумерандо и пренумерандо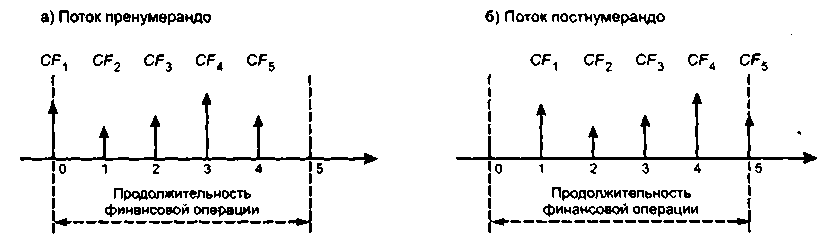

В каждой из приведенных на рис. 6.7 ситуаций финансовая операция, в ре­зультате которой будут иметь место притоки денежных средств CFk, осуществля­ется в виде пяти базисных периодов, при этом ее начало имеет место в начале 1 -го базисного периода (отмечено цифрой 0), а конец — в конце 5-го базисного перио­да (отмечено цифрой 5). По сравнению с (а) в случае (б) денежный поток как бы сдвинут влево на один интервал; это означает, что денежные притоки (или отто­ки) будут иметь место раньше.

На практике большее распространение получил поток постнумерандо; в част­ности, именно этот поток лежит в основе методик анализа инвестиционных проек­тов. Некоторые объяснения этому можно дать, исходя из общих принципов учета, согласно которым принято подводить итоги и оценивать финансовый результат того или иного действия по окончании очередного отчетного периода. Что касает­ся поступления денежных средств в счет оплаты, то на практике оно чаще всего распределено во времени неравномерно и потому удобнее условно отнести все по­ступления к концу периода. Благодаря этому соглашению формируются равные временные периоды, что позволяет разработать удобные формализованные алго­ритмы оценки. Поток пренумерандо имеет значение при анализе схем накопления денежных средств для последующего их инвестирования.

Практически любая финансовая операция (FO) может быть выражена в терми­нах денежного потока и описана следующей моделью;

Модель (6.22) может быть использована для оценки внутренней стоимости финансового актива, определения доходности финансовой операции или финансо­вого актива, расчета целесообразности принятия или непринятия инвестиционно го проекта и др. В основе соответствующих счетных алгоритмов — операции нара­щения и дисконтирования, связанные с оценкой соответствующего денежного по тока. Оценка потока может выполняться в рамках решения двух задач: (а) пря

мой, т. е. проводится оценка с позиции будущего (реализуется схема наращения):

(б) обратной, т. е. проводится оценка с позиции настоящего (реализуется схема дисконтирования).

Прямая задача предполагает суммарную оценку наращенного денежного пото­ка, т. е. в ее основе лежит будущая стоимость. В частности, если денежный поток представляет собой регулярные начисления процентов на вложенный капитал (Р) по схеме сложных процентов, то в основе суммарной оценки наращенного денеж­ного потока лежит формула (6.6), применяемая к каждому элементу потока.

Для наглядности приведем пример типовой ситуации. Предприниматель имеет возможность делать периодические взносы в банк в течение длительного периода и пытается оценить, какая сумма будет накоплена им к концу этого периода. По­добные расчеты представляют собой пример решения прямой задачи.

Обратная задача предполагает суммарную оценку дисконтированного (приве­денного) денежного потока. Поскольку отдельные элементы денежного потока ге­нерируются в разные временные интервалы, а деньги имеют временную ценность, непосредственное их суммирование невозможно. Дисконтирование денежного по­тока к одному моменту времени осуществляется с помощью формулы (6.20), при­меняемой к каждому элементу потока. Основным результатом расчета является определение общей величины приведенного денежного потока. Используемые при этом расчетные формулы различны в зависимости от вида потока — иостнумеран- до или пренумерандо.

Один из типовых примеров решения обратной задачи формулируется следую­щим образом. Инвестор имеет возможность получить в будущем серию платежей (доходы, проценты). Спрашивается: какую сумму готов заплатить инвестор сего­дня за возможность получения в будущем этой серии платежей?

Необходимо особо подчеркнуть, что ключевым моментом в рассмотренных схемах является предпосылка о том, что анализ ведется с позиции разумного ин­вестора, т. е. инвестора, не накапливающего полученные денежные средства в каком-нибудь сундуке, подобно небезызвестному Плюшкину, а немедленно инве­стирующего их с целью получения дополнительного дохода. Именно этим объяс­няется тот факт, что при оценке потоков в обоих случаях (при наращении и при дисконтировании) предполагается капитализация по схеме сложных процентов.