2. Дисконтированная стоимость единичного платежа

Оценивая целесообразность финансовых вложений в тот или иной вил бизне­са, исходят из того, является ли это вложение более прибыльным (при допусти­мом уровне риска), чем вложения в государственные ценные бумаги. Используя несложные методы, пытаются проанализировать будущие доходы при минималь­ном, безопасном уровне доходности.

Основная идея этих методов заключается в оценке будущих поступлений CF„ (например, в виде прибыли, процентов, дивидендов) с позиции текущего момен­та. При этом, сделав финансовые вложения, инвестор обычно руководствуется тремя посылами: (а) происходит перманентное обесценение денег (инфляция);

(б) темп изменения цен на сырье, материалы и основные средства, используемые предприятием, может существенно отличаться от темпа инфляции; (в) желатель­но периодическое начисление (или поступление) дохода, причем в размере не ниже определенного минимума. Базируясь на этих посылах, инвестор должен оценить, какими будут его доходы в будущем, какую максимально возможную сумму допустимо вложить в данное дело исходя из прогнозируемой его рента­бельности.

Ключевым в оценке подобных финансовых операций является умение оценки единичного платежа, ожидаемого к получению в будущем. Как уже отмечалось, здесь необходимо учесть фактор времени. В результате появляется понятие дис­контированной стоимости единичного платежа (Present Value of a Single Amount). Этим понятием обозначается оценка суммы, ожидаемой к получению в будущем, с позиции некоторого предшествующего момента времени. При этом предполагает­ся, что промежуток между этими временными моментами разделен на t равных интервалов (рис. 6.6). Чаще всего временные моменты О и и совпадают.

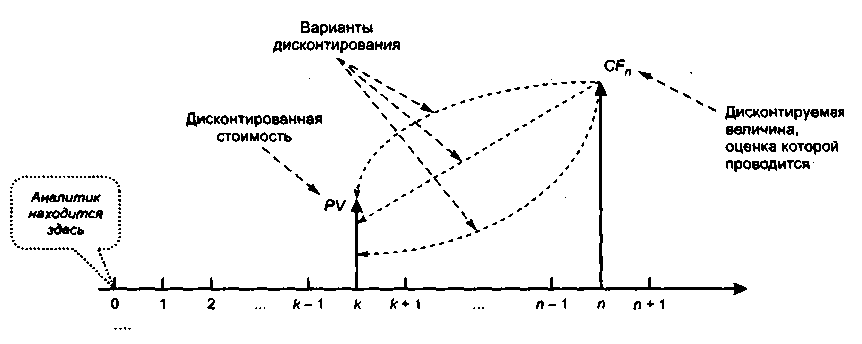
Рис. 6.6. Иллюстрация формирования дисконтированной стоимости

Подчеркнем, что но сути единичный платеж представляет собой частный слу­чай денежного потока {CF_k, k = t 2, ..., «}, когда CF_k = 0 при k п. В инвестици­онных расчетах, сопровождающих проекты инвестирования и финансирования базовой является схема сложных процентов, применяемая и для наращения, и для дисконтирования, а потому расчет дисконтированной стоимости ведется по фор­муле (6.20), являющейся следствием форму (6.6).

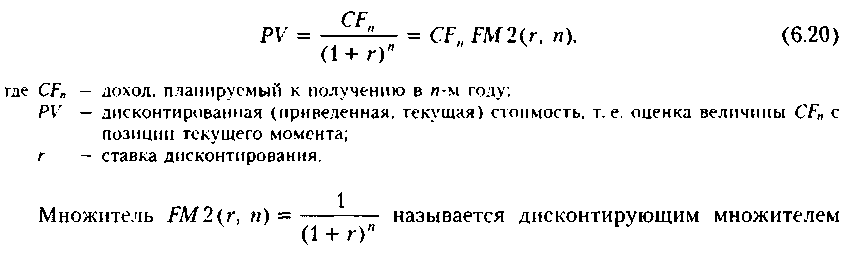
для единичного платежа. Как и в случае с множителем FM\(r, п), несложно по­нять, что значения дисконтирующего множителя не зависят от суммовых вели­чин, а потому их можно табулировать для различных комбинаций {г, «}, что обес­печивает упрощение расчетов на практике (см. Приложение 3). Экономиче­ский смысл дисконтирующего множителя FM2(r, п) заключается в следующем. Он показывает сегодняшнюю цену одной денежной единицы будущего, т. е. чему, с иозиции текущего момента, равна одна денежная единица (например, один рубль), циркулирующая в сфере бизнеса п периодов спустя от момента, на ко­торый осуществляется дисконтирование (обычно он совпадает с моментом рас­чета), при заданных процентной ставке (доходности) г и частоте начисления про­цента.

Величина дисконтированной стоимости зависит от ставки дисконтирования: чем больше ставка, тем меньше дисконтированная стоимость. Отсюда следует важный вывод: каждому фиксированному значению ожидаемой в будущем к полу­чению величины может соответствовать несколько значений дисконтированной стоимости, в зависимости от того, какая ставка дисконтирования выбрана анали­тиком. Иными словами, дисконтированная стоимость не есть жестко предопреде­ленная величина, она многозначна. Это свойство операции дисконтирования будет использоваться нами неоднократно при характеристике методов оценки финансо­вых активов.

Экономический смысл операции, проиллюстрированной на рис. 6.6, очевиден: величина PV означает оценку величины CF„ с позиции более раннего момента вре­мени; при этом принимается во внимание временная ценность денежных средств. Последнее означает, что PV практически всегда должна быть меньше CF„ (по­скольку знаменатель дроби больше единицы), т. е. РV означает более осторожную оценку обещаемой в будущем к поступлению величины CF„ (несложно понять, что совпадение величин CF„ и PV, привязанных к разным моментам времени, возмож­но лишь при г = 0).

В отношении отмеченных на оси абсцисс точек 0, к и п можно сказать следую­щее. В принципе, точка 0 может находиться в любом месте по отношению к ин­тервалу {£, /г}. Единственное условие, которое должно выполняться, таково: п > к. На практике чаще всего временные моменты 0 и k совпадают.

Как и в случае с наращением, дисконтирование может осуществляться с помо­щью разных функциональных зависимостей; кроме того, может по-разному дро­биться общая продолжительность финансовой операции на базисные периоды. Все это будет приводить к вполне естественному различию в результате дисконти­рования, т. е. сумма PV будет меняться. В финансовых операциях (особенно долго­срочного характера) в дисконтировании применяют схему сложных процентов, а базисным периодом считается год.

Пример

Инвестору через 4 года понадобится сумма 4500 тыс. руб. Один из вариантов ее накопления — банковский депозит. Какую сумму надо разместить на депозите, если банк предлагает ежегодное начисление процентов по ставке 12% годовых? Решение

Таким образом, в банк надо вложить 2862 тыс. руб., чтобы через 4 года полу­чить 4500 тыс. руб.: величина 2862 тыс. руб. представляет собой дисконтирован­ную стоимость величины 4500 тыс. руб. Для инвестора с учетом временного фак­тора и приемлемой доходности две эти величины равны по своей ценности.

Заметим, что если условия банка меняются, меняется и значение дисконтиро­ванной величины. Предположим, что договором предусматривается (1) полугодо­вое, (2) ежеквартальное начисление процентов. В этом случае значения дисконти­рованной стоимости будут соответственно равны: вариант (1)

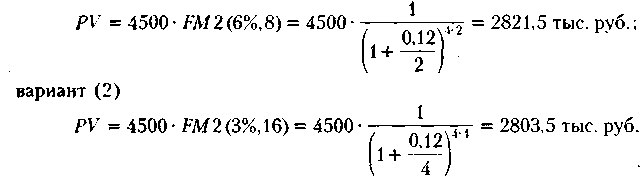
Видим, что более частое начисление процентов приводит к меныиему значе­нию дисконтированной стоимости. Это и понятно, поскольку ожидаемая и дис­контированная стоимости отличаются на величину процентов, сумма которых при использовании схемы сложных процентов тем больше, чем чаще идет начисление. Если инвестору доступно более частое начисление процентов, он дает и более ос­торожную оценку (т. е. дисконтированную стоимость) ожидаемого в будущем платежа. Степень осторожности в данном случае проявляется в относительном за­нижении дисконтированной стоимости.

Как уже отмечалось, дисконтирование означает, что для инвестора сумма PV в данный момент времени и сумма CF„ через п лет (в общем случае — базисных пе­риодов) одинаковы по своей ценности. А потому, используя формулу (6.20), мож­но приводить в сопоставимый вид оценку доходов от инвестиций, ожидаемых к поступлению в течение ряда лет. В этом случае ставка дисконтирования численно равна процентной ставке, устанавливаемой инвестором, т. е. тому относительному размеру дохода, который инвестор хочет или может получить на инвестируемый им капитал.

Определяя ставку дисконтирования, обычно исходят из так называемого безо­пасного, или гарантированного, уровня доходности финансовых инвестиций, кото­рый обеспечивается государственным банком по вкладам или при операциях с ценными бумагами. При этом может даваться надбавка за риск, причем чем более рисковым считается рассматриваемый проект или финансовый контракт, тем больше размер премии за риск. Процентная ставка rd, используемая в качестве ставки дисконтирования, будет в этом случае иметь следующий вид:

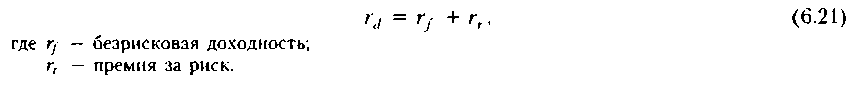
Пример

На вашем счете в банке 200 тыс. руб. Банк платит 11% годовых. Вам предла­гают войт» всем вашим капиталом в организацию венчурного предприятия. Пред­ставленные экономические расчеты показывают, что через 6 лет ваш капитал уд­воится. Стоит ли принимать это предложение?

Решение

Оценка данной ситуации может быть сделана либо с позиции будущего, либо с позиции настоящего. В первом случае анализ основан на сравнении двух сумм — получаемых от вложения в рисковое предприятие и в банковское учреж­дение с гарантированным доходом. Первая сумма равна 400 тыс. руб., вторая на­ходится по формуле (6.6):

Приведенный расчет свидетельствует об экономической выгоде сделанного вам предложения. Однако необходимо по возможности учесть фактор риска.

Второй вариант анализа основан на дисконтированных оценках. Предпо­ложим, что финансовый консультант рекомендует оценить риск участия в вен­чурном предприятии путем введения премии в размере 3% к безрисковой до­ходности, т. е. к ставке, обещаемой банком. Таким образом, ставка дискон­тирования будет равна 14%. Тогда по формуле (6.20) можно рассчитать при­веденную стоимость ожидаемого поступления (PV⁷) при участии в венчурном предприятии:

Иными словами, вы вложите в венчурное предприятие 200 тыс. руб., а обрат­но получите сумму, дисконтированная стоимость которой равна 182,4 тыс. руб., т. е. меньше величины исходной инвестиции. Инвестиция не окупается. При та­ких исходных посылах предложение об участии в венчурном предприятии для вас невыгодно.