4. Будущая и дисконтированная стоимости: экономический смысл и техника расчета

В предыдущих разделах главы мы ознакомились с логикой операций нараще­ния и дисконтирования, с разными схемами их реализации. В дальнейшем мы увидим, что в числе ключевых аспектов деятельности финансового менеджера яв­ляется умение оценивать некоторый платеж (или последовательность платежей) с позиции настоящего и будущего. Поэтому прежде всего обобщим приведенные в предыдущих разделах сведения о таких понятиях, как будущая и дисконтирован­ная стоимости.

1. Будущая стоимость единичного платежа

Рассмотрим более подробно сущность будущей стоимости как одного из клю­чевых понятий в финансовых вычислениях. Существуют различные ее определе­ния. В частности, под будущей стоимостью (Future Value) можно понимать стои­мость в некоторый момент времени, рассматриваемую с позиции будущего, при условии ее наращения по некоторой ставке. Можно дать иное определение: буду­щая стоимость — это сумма первоначального капитала и начисленного на него процентного дохода, получаемая в результате осуществления процесса наращения в течение и базисных периодов (n > l) по ставке г. Сразу же заметим, что нараще­ние может осуществляться с применением разных схем. В специальной литерату­ре иногда используется синоним — «наращенная стоимость» (Accumulated Value). Данное понятие применяется в отношении как единичного платежа, так и денеж­ного потока, т. е. серии платежей.

Подавляющее большинство финансовых операций в экономике представляют собой комбинации двух типовых процессов — мобилизации финансовых ресурсов и их инвестирования. В любом случае подразумевается, что предоставленные ре­сурсы должны быть не только возвращены, но должны принести определенный доход кредитору. Отсюда возникает необходимость в расчете будущей стоимости инвестируемой суммы как ответ на вопрос, а стоит ли участвовать в данной фи­нансовой операции. Величина вознаграждения зависит от трех параметров:

(а) продолжительности финансовой операции, (б) процентной ставки, (в) схемы начисления вознаграждения. Очевидно, что критическую роль играет процентная ставка: если г — О, то независимо от двух других параметров инвестируемая и воз­вращаемая суммы окажутся равными.

Понятие будущей стоимости особенно широко используется при оценке целе­сообразности некоторой инвестиции. Дело в том, что любая инвестиция представ­ляет собой вложение денежных средств (прямо или косвенно) в надежде, что в бу­дущем инвестор сможет получить определенный доход, оправдывающий омертв­ление исходной суммы в данной инвестиции. Поскольку возможностей инвести­рования обычно много, возникает вопрос о предпочтительности того или иного варианта. Один из способов решения этого вопроса — расчет будущей стоимости исходной инвестиции в условиях сравниваемых вариантов инвестирования.

Если PV — это исходная сумма денежных средств, инвестированная в некото­рый проект на срок п базисных периодов, a FV — сумма, полученная как нараще­ние величины PV по некоторой ставке г, то FV как раз и будет трактоваться как будущая стоимость величины PV (рис. 6.5). Прежде всего необходимо сделать два замечания.

Рис. в. 5. Иллюстрация формирования будущей стоимости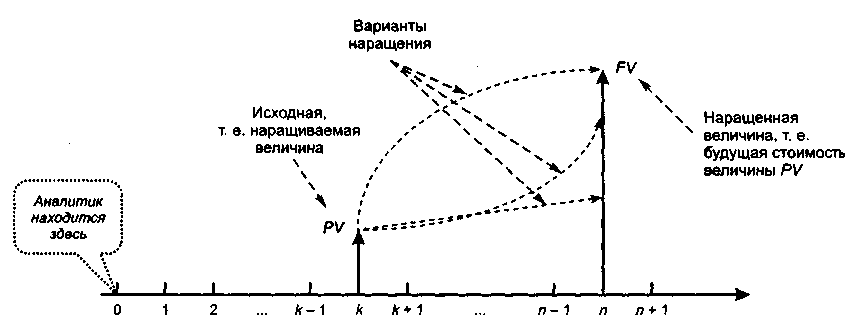

Во-первых, как видно из рисунка, наращение может осуществляться с помо­щью различных функциональных зависимостей; кроме того, может по-разному дробиться общая продолжительность финансовой операции на базисные периоды. Все это будет приводить к вполне естественному различию в результате нараще­ния, т. е, сумма FV будет меняться. В финансовых операциях (особенно долгосроч­ного характера) в наращении обычно применяют схему сложных процентов, а ба­зисным периодом считается год. На практике, однако, наибольшее распростране­ние получили два типовых варианта наращения, известных как схема простых процентов и схема сложных процентов. В первом случае не предполагается капи­тализации процентов, во втором — она предполагается, т. е. базой для очередного начисления процентов является не только исходная сумма PV, но и ранее начис­ленные проценты.

Во-вторых, на рис. 6.5 выделено три ключевых момента времени:

• в точке 0 находится аналитик;

• в точке к находится наращиваемая величина PV;

• в точке п находится будущая стоимость исходной величины PV.

В принципе точка 0 может находиться в любом месте но отношению к интер­валу {&, и}. Единственное условие, которое должно выполняться, таково: п > к. На практике чаще всего временные моменты 0 и к совпадают.

Экономический смысл величины FV таков: FV представляет собой сумму, ко­торую инвестор хотел бы получить по окончании финансовой операции, в кото­рую он вложил сумму PV. Иными словами, с учетом временной ценности денег и устраивающей инвестора нормы прибыли суммы PV «сегодня» и FV «завтра» рав­ны по своей ценности.

Можно привести следующий образный пример. Предположим, что работнику предлагают выбрать вариант оплаты его работы: (a) PV руб. сегодня; (б) FV руб. через некоторое время в будущем. Если процентная ставка устраивает работника, т. е. рассматривается им как оптимальная, которую он всегда и без риска сможет получить, то ему безразличен выбор между величинами PV и FV (заметим, что ставка г в данном случае играет роль показателя эффективности).

Строго говоря, при обосновании целесообразности некоторой финансовой опе­рации в терминах величин PV ** FV предполагается, что потребности текущего по­требления удовлетворены, и во внимание принимается чисто инвестиционный ас­пект этой операции (если сумма PV «сегодня» нужна для того, чтобы, образно го­воря, не умереть с голоду, то, естественно, ни о какой FV «завтра» уже речи идти не может).

Что касается техники расчета будущей стоимости, то она должна задаваться кредитором. Это вполне естественно, поскольку тот, кто предоставляет денежные средства в долг (иначе: инвестирует их), имеет право определять и величину воз­награждения за это. Однако на практике данное утверждение выполняется далеко не всегда. Так, банки, принимая вклады и выступая по сути в роли заемщика, сами задают процентные ставки и схемы начисления. Обосновывается это тем, что банк акцентирует внимание на функции сбережения, т. е. он предоставляет услугу клиенту по сохранению его средств, но поскольку банк все же использует эти средства в своих инвестиционных проектах, он предлагает клиенту некоторое воз­награждение. Как мы видели ранее, основными являются две схемы наращения — простых и сложных процентов. В долгосрочных проектах инвестирования и фи­нансирования естественным является применение схемы сложных процентов; в этом случае базовой расчетной формулой является формула (6.10).