3. Внутригодовые процентные начисления

В практике выплаты доходов на вложенный капитал нередко оговариваются величина годового процента и количество периодов начисления процентов. В этом случае расчет наращенной суммы FV„ ведется по формуле сложных процентов по

подынтервалам и но ставке, равной пропорциональной доле исходном годовом ставки, по формуле

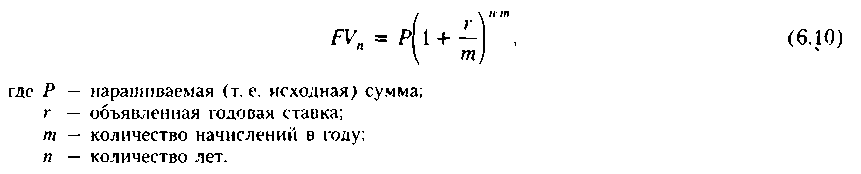
Вновь обращаем внимание читателя на то обстоятельство, что в формулах на­ращения и дисконтирования должно соблюдаться соответствие между процентной ставкой и продолжительностью базисного периода. Так, переход от годового на­числения процентов к квартальному (т = 4) предполагает переход к квартальной ставке, что как раз и имеет место в формуле (6.10).

Пример

В условиях предыдущего примера проанализировать, изменится ли величи­на капитала к копну 2-летнего периода, если бы проценты начислялись ежеквар­тально.

В этом случае начисление будет проводиться 8 раз по ставке сумма к концу 2-летнего периода составит

Таким образом, можно сделать несколько практических выводов:

• при начислении процентов: 12% годовых не эквивалентно 1% в месяц (по­добное ошибочное отождествление довольно распространено среди начинаю­щих бизнесменов);

• чем чаще идет начисление но схеме сложных процентов, тем больше итого­вая накопленная сумма (обращаем внимание на то, что речь идет не о выпла­те, а о начислении).

Заметим, что для простых процентов такие выводы не имеют места. Одно из характерных свойств наращения по простым процентам заключается в том, что наращенная сумма не изменяется с увеличением частоты начислений простых процентов. Например, наращение простыми процентами ежегодно но ставке 10% годовых дает тот же результат, что и ежеквартальное наращение простыми про­центами по ставке 2,5% за квартал. При наращении по сложным процентам еже­квартальное начисление доставляет больший результат, чем ежегодное.

4. Начисление процентов за дробное число лет

Довольно обыденными являются финансовые контракты, заключаемые на пе­риод, отличающийся от целого числа лет. В этом случае проценты могут начис­ляться одним из двух методов:

Возможны финансовые контракты, в которых начисление процентов осуществ­ляется по внутригодовым подпериодам, а продолжительность общего периода дей­ствия контракта не равна целому числу подпериодов. В этом случае также воз­можно использование двух схем наращения исходной суммы Р:

1} схема сложных ппоиентов

• по схеме сложных процентов

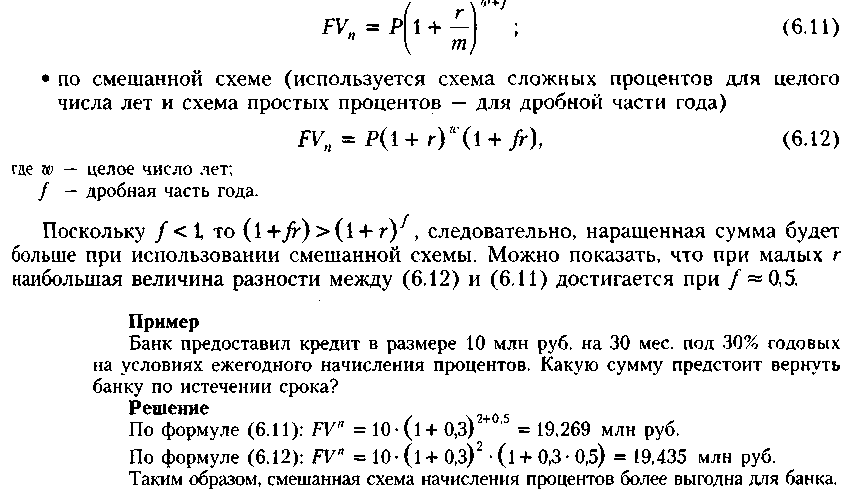
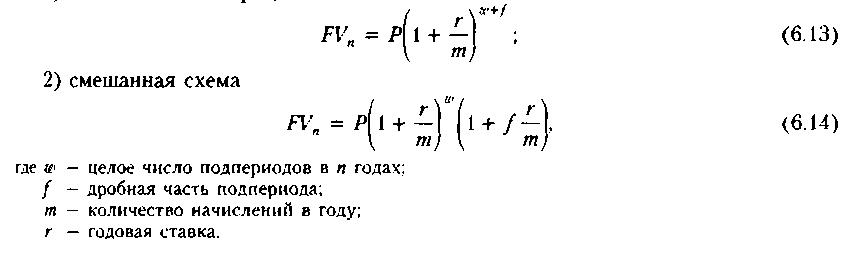
5. Непрерывное начисление процентов

Все рассмотренные выше проценты называются дискретными, поскольку их начисление осуществляется за фиксированный промежуток времени (год, квартал, месяц, день, даже час). Уменьшая этот промежуток (период начисления) и увеличивая частоту начисления процентов, можно перейти к так называемым непрерывным процентам.

Чтобы отличить непрерывную ставку от обычной (дискретной), вводят специ­альное обозначение непрерывной ставки — S и называют ее силой роста. Таким образом, формула для нахождения наращенной суммы за п лет при непрерывном начислении процентов принимает вид

Формулой (6.15) пользуются и в тех случаях, когда и не является целым чис­лом. Таким образом, при непрерывном начислении процентов в пределах одного года используется следующая базовая формула:

Пример

Рассчитать накопленную сумму для различных вариантов начисления про­центов за один год, если исходная сумма Р = 1000 руб. и г = 10%.

Решение

Результаты, полученные для некоторых вариантов, приведем в виде таблицы, причем в предпоследнем столбце вычислены разности между наращениями с дан­ным числом начисления процентов и базисным, а в последнем столбце указаны разности между наращенными суммами двух соседних строчек.

Уже отмечалось, что в зависимости от частоты начисления процентов нараще­ние суммы осуществляется разными темпами, причем с возрастанием частоты на­копленная сумма увеличивается. Максимально возможное наращение осуществля­ется при бесконечном дроблении годового интервала. Из формулы (6.10) следует

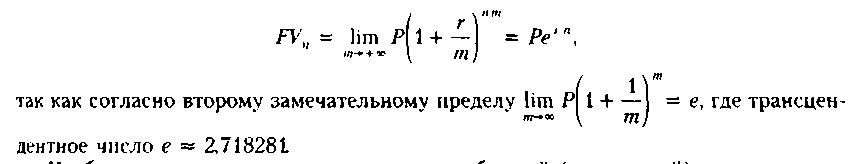
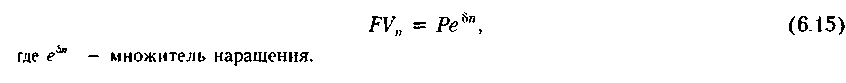
Как и следовало ожидать, приведенные расчеты подтверждают наличие пря­мой зависимости между частотой начисления процентов и накопленной суммой. Последний столбец таблицы показывает, что с увеличением частоты начисления темп прироста накопленной суммы уменьшается. В частности, видно, что переход от ежедневного к непрерывному начислению процентов не имеет какого-либо зна­чимого эффекта.

Изменение накапливаемой суммы в зависимости от частоты начисления пока­зано на рис. 6.4. Сравнительная характеристика и интерпретация приведенных гра­фиков очевидны, вместе с тем эти графики позволяют наглядно представить влия­ние частоты начисления процентов. При дискретном наращении каждая ступенька характеризует прирост основной суммы в результате очередного начисления, при­чем величина ступеньки все время возрастает. В рамках одного года одной сту­пеньке на левом графике соответствуют две ступеньки на среднем графике мень­шего размера, однако в сумме они превышают эту ступеньку однократного начис­ления. Таким образом, ордината точки, соответствующей концу трехлетнего перио­да, на среднем графике будет выше, чем на левом. Еще более быстрым темпом идет наращение ири непрерывном начислении, что и показывает график справа.

Рис. 6.4. Различные варианты начисления процентов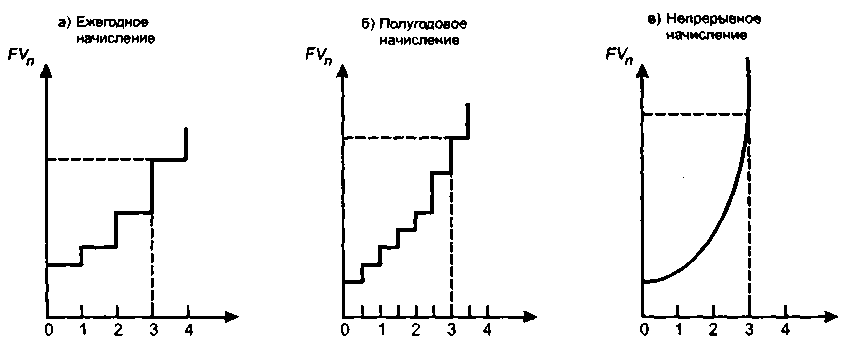

Несложно найти связь между силой роста 8 и годовой процентной ставкой г в случае однократного начисления процентов в рамках одного года (и = 1, т = 1). Применение 5 и г к одной и той же исходной сумме Р должно дать одинаковый результат FV. Приравнивая наращенные суммы в формулах (6.10) и (6.16), полу­чим

Непрерывное начисление процентов может использоваться при анализе сложных финансовых задач (например, обоснование и выбор инвестиционных решений). Оценивая работу финансового учреждения за период, в котором платежи поступают многократно, целесообразно предполагать, что накапливаемые суммы непрерывно меняются во времени, и применять непрерывное начисление процентов.

Бывают ситуации, когда непрерывное начисление процентов применяется непосредственно при работе с клиентами. Так, в начале 1975 г. в США [Шарп, Александер, Бэйли, с. 140] ставка процентных выплат но займам и депозитам сро­ком 6—10 лет была ограничена величиной 7,75% годовых, однако не лимитирова­лось число начислений процентов в течение года, чем и воспользовались компа­нии в целях привлечения вкладчиков. Одна из компаний предлагала непрерывное начисление процентов при годовой ставке 7,75%, которая в этих условиях стала непрерывной и представляла собой силу роста. Обозначая 5 = 0,0775, получим г=б'^0,0775— 1= 1,0806, т. е. компания установила процентную годовую ставку /' = 8,06%.