2. Области применения схемы простых процентов

На практике многие финансовые операции выполняются в рамках одного года, при этом могут использоваться различные схемы и методы начисления процентов. Рассмотрим часто встречающиеся ситуации, когда активно применяется схема простых процентов.

Краткосрочный кредит. В этом случае денежные средства заемщику предос­тавляются на срок до одного года и, как правило, с однократным начислением процентов. Как отмечалось выше, в этом случае для кредитора, диктующего чаще всего условия финансового контракта, более выгодна схема простых процентов; при этом в расчетах используют промежуточную процентную ставку, которая рав­на доле годовой ставки, пропорциональной доле временного интервала в году.

Общий алгоритм наращения некоторой исходной суммы по схеме простых процентов при заданной доходности г (в долях единицы) описывается форму­лой (6.5). Если п < 1 (это, напомним, и есть ситуация, когда схема простых про­центов более предпочтительна по сравнению со схемой сложных процентов), фор­мулу (6.5) можно представить следующим образом:

Для понимания сути краткосрочной операции наращения капитала, вероятно, наиболее наглядно последнее представление в (6.7), из которого видно, что получае­мое по итогам операции наращение рассчитывается умножением исходного капитала

Р на произведение дневной ставки на продолжительность финансовой операции

(t). Заметим в этой связи, что в представлении (6.7) выполнено упоминавшееся в комментарии к формулам (6.1) и (6.2) правило о соответствии ставки и периода; про­должительность операции оценена в днях, потому сделан переход к дневной ставке.

Определяя продолжительность финансовой операции, принято день выдачи и день погашения кредита считать за один день. В зависимости от того, чему берет­ся равной продолжительность года (квартала, месяца), размер промежуточной процентной ставки может быть различным. Возможны два варианта:

• точный процент, определяемый, исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);

• обыкновенный процент, определяемый, исходя из приближенного числа дней в году, квартале и месяце (соответственно 360, 90, 30).

При определении продолжительности периода, на который выдан кредит, так­же возможны два варианта:

• принимается в расчет точное число дней пользования кредитом (расчет ве­дется по дням);

• принимается в расчет приблизительное число дней пользования кредитом (исходя из продолжительности месяца в 30 дней).

Для упрощения процедуры расчета точного числа дней пользуются специаль­ными таблицами (одна для обычного года, другая — для високосного), в которых все дни в году последовательно пронумерованы. Продолжительность финансовой операции определяется вычитанием номера первого дня из номера последнего дня (см. Приложение 4).

В том случае, когда в расчетах используется точный процент, берется и точная величина продолжительности финансовой операции; при использовании обыкно­венного процента может применяться как точное, так и приближенное число дней пользования кредитом. Таким образом, расчет может выполняться одним из трех способов:

• обыкновенный процент с точным числом дней (применяется в Бельгии, Франции);

• обыкновенный процент с приближенным числом дней (Германия, Дания, Швеция);

• точный процент с точным числом дней (Великобритания, США).

В практическом смысле эффект от выбора того или иного способа зависит от значительности суммы, фигурирующей в финансовой операции. Но и так ясно, что использование обыкновенных процентов с точным числом дней ссуды, как правило, дает больший результат, чем применение обыкновенных процентов с приближенным числом дней пользования кредитом.

Пример

Предоставлен кредит в размере 7 млн руб, 10 февраля с погашением 10 июня под 20% годовых (год невисокосный). Рассчитать разными способами сумму к по­гашению (FV).

Решение

Величина уплачиваемых за пользование кредитом процентов зависит от числа дней, которое берется в расчет. Точное число дней определяется по таблице с номе­рами дней года (см. Приложение 4): 161 —41 = 120 дн. Приближенное число дней кредита рассчитывается следующим образом: 18 дней февраля (59 —41)+ 90 дн. (по 30 дней каждого из трех месяцев: март, апрель, май) + 10 дней июня - 118 дн.

Возможные варианты возврата долга определяются с помощью формулы

(6.7):

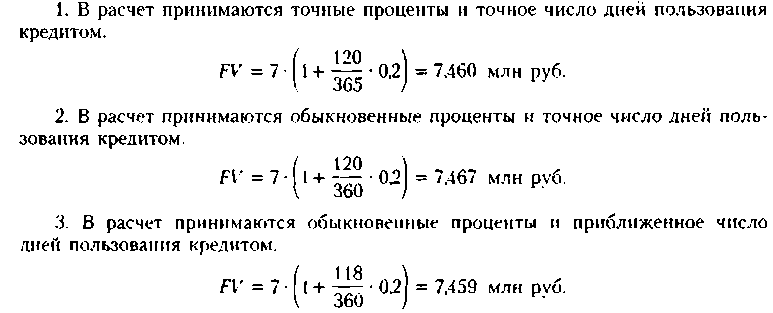
Векселедержатель предъявил для учета вексель на сумму 50 тыс. руб. со сро­ком погашения 28.09.2006 г. Вексель предъявлен 13.09.2006 г. Банк согласился учесть вексель по учетной ставке 30% годовых. Определить сумму, которую век­селедержатель получит от банка.

Величина этой суммы рассчитывается по формуле (6.8) и составит

Разность между FV (номинальной величиной векселя) и PV (дисконтирован­ной величиной векселя) представляет собой комиссионные, удерживаемые бан­ком в свою пользу за предоставленную услугу; в данном примере она составила 625 руб.

Учет векселя банком. Это еще одна весьма распространенная операция крат­косрочного характера, для оценки которой используется схема простых процентов, с тем лишь отличием, что в расчете применяется дисконтная ставка. Одна из при­чин состоит в том, что векселя могут оформляться по-разному, однако чаще всего банку приходится иметь дело с суммой к погашению, т. е. с величиной FV. Схема действий в этом случае может быть следующей.

Пример

Владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его, т. е. купить, удерживая в свою пользу часть вексельной суммы, которая нередко также называется дисконтом. В этом случае банк предлагает владельцу сумму (PV), исчисляемую, исходя из объявленной банком ставки дисконтирова­ния (</). Очевидно, что чем выше значение дисконтной ставки, тем большую сум­му удерживает банк в свою пользу. Расчет выдаваемой банком суммы ведется с помощью одного из представлений формулы (6.8), являющейся следствием фор­мулы (6.4):

Можно выполнить и более глубокий факторный анализ. Дело в том, что доход банка при учете векселя складывается из двух частей: процентов по векселю, при­читающихся за время, оставшееся до момента погашения векселя, и собственно комиссионных за предоставленную услугу. Как уже упоминалось выше, теорети­ческая дисконтная ставка меньше процентной. Однако на практике, устанавливая дисконтную ставку, банк, как правило, повышает ее в зависимости от условий, на которых выдан вексель, риска, связанного с его погашением, комиссионных, кото­рые банк считает целесообразным получить за оказанную услугу, и т. п. Посколь­ку величина процентов по векселю за период с момента учета до момента погаше­ния предопределена, банк может варьировать лишь размером комиссионных пу­тем изменения учетной ставки. Прежде чем рассмотреть пример, изложим логику факторного анализа дохода банка в этом случае.

Введем следующие обозначения: PV — стоимость векселя в момент его оформ­ления; Р\ — теоретическая стоимость векселя в момент учета; Рг — предлагаемая банком сумма в обмен на вексель; FV — стоимость векселя к погашению; Л,, — об­щий доход банка от операции.

Рис. 6.3. Логика факторного разложения дохода банка при учете векселя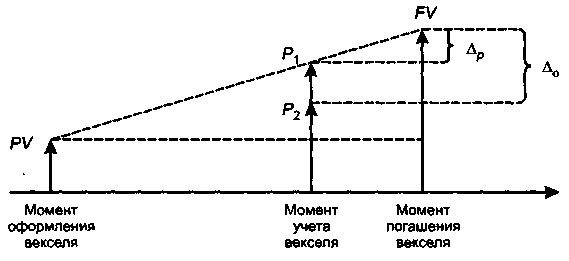

Скорость наращения стоимости векселя, т. е. наклон прямой {PV, /У}, зависит от уровня процентной ставки г, согласованной между векселедателем и векселе­держателем. По мере приближения срока погашения векселя его теоретическая стоимость постоянно возрастает на сумму причитающихся за истекший период процентов; таким образом, в момент учета векселя она составит величину Р\, кото­рую можно рассчитать по формуле (6.7). Таким образом, учитывая вексель в бан­ке, его владелец теоретически мог бы рассчитывать на сумму Pi, а факт ее получе­ния означай бы, что с момента учета векселя кредитором векселедателя фактиче­ски становится банк. Вряд ли такое положение устраивает менеджеров банка, по­скольку не очевидно, что заложенная в векселе доходность в размере ставки г будет привлекательна для банка. Именно поэтому предлагаемая банком сумма Р2, которая рассчитывается по формуле (6.8), исходя из стоимости векселя к погаше­нию и предлагаемой банком дисконтной ставки d, в принципе не связанной со ставкой г, в подавляющем большинстве случаев меньше теоретической стоимости векселя. Разность Д ₍ = (Р, — Р₂) представляет собой сумму комиссионных, полу­чаемых банком за услугу, оказываемую векселедержателю. С позиции последнего, эта сумма представляет собой затраты, т. е. плату за возможность более быстрого получения наличных. Помимо комиссионных банк получает проценты за период с момента учета до момента погашения векселя, сумма которых рассчитывается по формуле: А_р = FV - Р_{. Таким образом, общий доход банка от операции составит Д „ = Д_р + A_f — FV — Р₂. Отметим, что реальные потери векселедержателя со­ставляют величину Д _г = - Р₂, а не сумму (FV — Р₂), как это кажется на пер­

вый взгляд. Дело в том, что с момента учета векселя кредитором становится банк, поэтому ему и передаются проценты за оставшийся период.

Пример

Предприятие продало товар на условиях потребительского кредита с оформ­лением простого векселя: номинальная стоимость 150 тыс. руб., срок векселя — 60 дней, ставка процента за предоставленный кредит — 15% годовых. Через 45 дней с момента оформления векселя предприятие решило учесть вексель в банке; предложенная банком дисконтная ставка составляет: (1) 20%; (2) 25% го­довых. Рассчитать суммы, получаемые предприятием и банком, если используют­ся обыкновенные проценты с точным числом дней.

Дисконтирование, осуществляемое по формуле (6.8), называется банковским дисконтированием, в отличие от математического дисконтирования, являющегося процессом, обратным к наращению первоначального капитала. При математиче­ском дисконтировании решается задача нахождения такой величины капитала Р, которая через п лет при наращении по схеме простых процентов по процентной ставке г будет равна R,,. Решая (6.5) относительно Р, получим