2. Процентные ставки и методы их начисления

Ссудозаемные операции, составляющие основу коммерческих вычислений, имеют давнюю историю. Именно в этих операциях и проявляется прежде всего необходимость учета временной ценности денег. Несмотря на то что в основе рас­четов при анализе эффективности ссудозаемных операций заложены простейшие, на первый взгляд, схемы начисления процентов, эти расчеты многообразны ввиду вариабельности условий финансовых контрактов в отношении частоты и способов начисления, а также вариантов предоставления и погашения ссуд.

1. Понятия простого и сложного процентов

Предоставляя свои денежные средства в долг, их владелец получает опреде­ленный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Поскольку стандартным временным интерва­лом в финансовых операциях является один год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Из­вестны две основные схемы дискретного начисления: схема простых процентов (simple interest) и схема сложных процентов (compound interest).

Схема простых процентов предполагает неизменность базы, с которой проис* ходит начисление. Пусть исходный инвестируемый капитал равен Р, требуемая доходность — г (в долях единицы). Считается, что инвестиция сделана на услови­ях простого процента, если инвестированный капитал ежегодно увеличивается на величину Рг. Таким образом, размер инвестированного капитала (R„) через и лет будет равен

Считается, что инвестиция сделана на условиях сложною процента, если оче­редной годовой доход исчисляется не с исходной величины инвестированного ка­питала, а с общей суммы, включающей ранее начисленные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т. е. база, с которой начисляются проценты, все время возрас­тает. Следовательно, размер инвестированного капитала будет равен

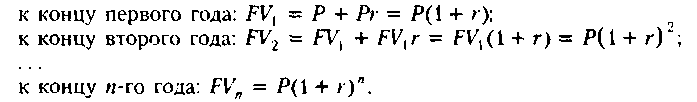
Как же соотносятся величины R„ и FV_n? Это чрезвычайно важно знать при проведении финансовых операций. Все зависит от величины п. Сравним множите­ли наращения по простым и сложным процентам, т. е. сравним (1 + пг) и (1 + г)”. Очевидно, что при п — 1 эти множители совпадают и равны (1 + г). Можно пока-

Рис. 6.2. Простая и сложная схемы наращения капитала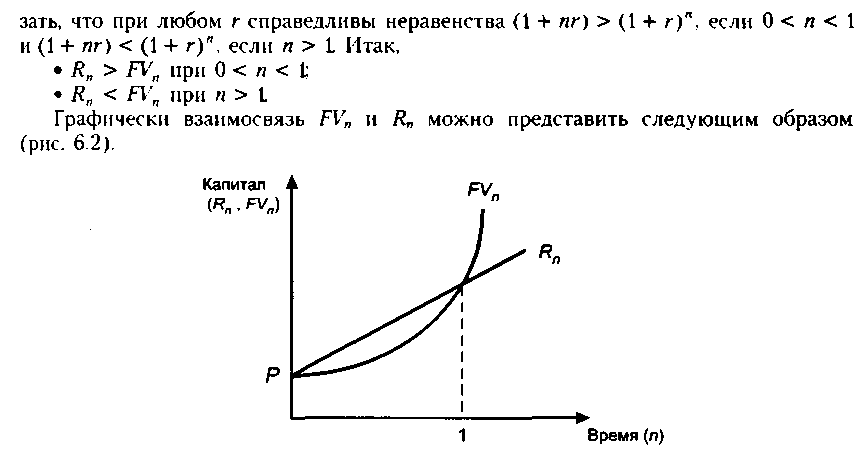

Таким образом, в случае ежегодного начисления процентов для лица, предос­тавляющего кредит:

• более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода):

• более выгодной является схема сложных процентов, если срок ссуды превы­шает один год (проценты начисляются ежегодно);

• обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

В случае краткосрочных ссуд со сроком погашения до одного года в качестве показателя п берется величина, характеризующая удельный вес длины подиериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина различных вре­менных интервалов в расчетах может округляться: месяц — 30 дней; квартал — 90 дней; полугодие — 180 дней; год — 360 (365 или 366) дней.

Пример

Рассчитать наращенную сумму с исходной суммы в 1 тыс. долл. при размеще­нии ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 20%; б) периоды наращения: 90 дней, 180 дней, 1 год, 5 лет, 10 лет. Полагать, что в году 360 дней.

Результаты расчетов имеют следующий вид.

Таким образом, если денежные средства размещены в банке на срок 90 дней (менее одного года), то наращенная сумма составит: при использовании схемы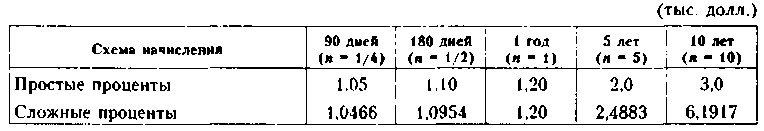

простых процентов — 1,05 тыс. долл.; при использовании схемы сложных процен­тов — 1,0466 тыс. долл. Следовательно, более выгодна первая схема (разница — 3,4 долл.). Если срок размещения денежных средств превышает один год. ситуа­ция меняется диаметрально: более выгодна схема сложных процентов, причем на­ращение в этом случае идет очень быстрыми темпами. Так, при ставке в 20% го­довых удвоение исходной суммы происходит следующим темпом: при использо­вании схемы простых процентов за 5 лет, а при использовании схемы сложных процентов — менее чем за 4 года.

Использование в расчетах сложного процента в случае многократного его на­числения более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их на­числения целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.

Итак, формула наращения по схеме сложных процентов имеет вид

Множитель FMl(r, п) = (1 + г)” инвариантен по отношению к суммовым вели­чинам, а потому для удобства пользования его можно табулировать для различ­ных комбинаций г и п (см. Приложение 3), Этот множитель называется мультип­лицирующим множителем для единичного платежа. Формула сложных процентов является одной из базовых формул в финансовых вычислениях.

Экономический смысл множителя FM 1(г, п): он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т. п.) через п перио­дов при заданной процентной ставке г, т. е. он оценивает будущую стоимость од­ной денежной единицы. Подчеркнем, что при пользовании этой и последующими финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки. Так, если базисным периодом начисления процентов является квартал, то в расчетах должна использоваться квартальная ставка.

В практических расчетах для наглядной и быстрой оценки эффективности предлагаемой ставки наращения при реализации схемы сложных процентов поль­зуются приблизительным расчетом времени, необходимого для удвоения инве­стированной суммы, известным как правило 72-х. Это правило заключается в

следующем: если г — процентная ставка, выраженная в процентах, то

представляет собой число периодов, за которое исходная сумма приблизительно удвоится. Это правило хорошо срабатывает для небольших значений г (до 20%). Так, если годовая ставка г = 12%, то к = 6 годам. Подчеркнем, что здесь речь идет о периодах начисления процентов и соответствующей данному периоду ставке. Если базисным периодом, т. е. периодом наращения, является половина года, то в расчете должна использоваться полугодовая ставка. Следует также обратить внимание на то, что хотя в большинстве финансовых расчетов процентная ставка берется в долях единицы, в формуле алгоритма правила 72-х ставка взята в про­центах.