2. Оценка аннуитета с изменяющейся величиной платежа

На практике возможны ситуации, когда величина платежа меняется со време­нем в сторону увеличения или уменьшения. В частности, при заключении догово­ров аренды в условиях инфляции может предусматриваться периодическое увели­чение платежа, компенсирующее негативное влияние изменения цен. Оценка ан­нуитета в этом случае может выполняться путем несложных расчетов с помощью финансовых таблиц. Технику вычислений рассмотрим на примере.

Пример

Сдан участок в аренду на 10 лет. Арендная плата будет осуществляться ежегод­но по схеме постнумерандо на следующих условиях: в первые 6 лет по 10 тыс. долл., в оставшиеся 4 года по 11 тыс. долл. Требуется оценить дисконтированную стои­мость этого договора, если процентная ставка, используемая аналитиком, равна 15%.

Решение

Решать данную задачу можно разными способами, в зависимости от того, ка­кие аннуитеты будут выделены аналитиком. Общая схема денежного потока пред­ставлена на рис. 6.14.

Рис. в. 14. Аннуитет с изменяющейся величиной платежа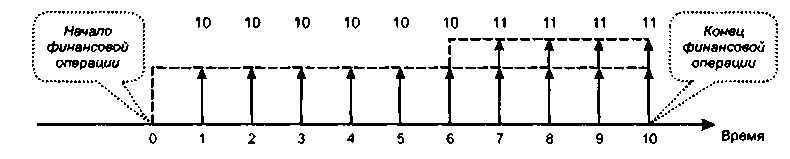

Прежде всего отметим, что дисконтированная стоимость денежного потока должна оцениваться с позиции начала первого временного интервала. Рассмотрим два варианта решения из нескольких возможных. Все варианты основываются на свойстве аддитивности рассмотренных алгоритмов в отношении величины аннуи­тетного платежа.

• Исходный поток можно представить себе как сумму двух аннуитетов: первый имеет А = 10 и продолжается 10 лет; второй имеет А = 1 и продолжается 4 года. По формуле (6.35) можно оценить дисконтированную стоимость каждого аннуитета. Однако второй аннуитет в этом случае будет оценен с позиции начала 7-го года, поэтому полученную сумму (т. е. единичный платеж) необходимо дисконтировать с помощью формулы (6.20) к началу 1-го года. В этом случае оценки двух аннуитетов будут приведены к одному моменту времени, а их сумма даст оценку дисконтированной стоимости исходного денежного потока.

• Исходный поток можно представить себе как разность двух аннуитетов: первый имеет А = 11 и продолжается 10 лет; второй имеет А — 1 и, начавшись в i-м году, заканчивается в 6-м. В этом случае расчет выглядит так:

Очевидно, что итоговый результат не зависит от способа расчета. Экономиче­ский смысл расчетов заключается в следующем. На момент начала действия догово­ра его ценность равна 51,42 тыс. долл., т. е. за эту сумму можно было бы продать данный договор. С учетом временной ценности денег и приемлемости процентной ставки в 15% (как отдачи на вложенный капитал) единовременно получаемая сумма 51,42 тыс. долл. равносильна получению в течение 11 лет серии оговоренных плате­жей (в первые 6 лет по 10 тыс. долл., в оставшиеся 4 года по 11 тыс. долл.).

6.8. Логика оценки денежного потока в нетиповых ситуациях

Как следует из приведенных выше рассуждений, величина оценки любого де­нежного потока вариабельна и зависит от ряда более или менее очевидных факто­ров, параметров, условий и ситуаций. К очевидным параметрам относятся прогно­зируемая продолжительность потока, величины прогнозируемых притоков (отго- ков), задаваемая процентная ставка (или ставки), принимаемая к расчету схема наращения или дисконтирования. К числу неочевидных, но весьма реалистичных ситуаций относится ситуация, когда имеет место несовпадение моментов начисле­ния процентов и поступления платежей. Например, требуется оценить величину аннуитета продолжительностью 5 лет, при этом аннуитетные платежи поступают ежеквартально, а начисление процентов ведется раз в год. Несложно понять, что в общем случае возможны три ситуации:

• моменты поступления платежей и моменты начисления процентов совпада­ют, т. е. поступления и начисления осуществляются с одинаковой частотой (например, полугодовые поступления и полугодовое начисление процентов);

• платежи поступают более часто по сравнению с начислением процентов (на­пример, полугодовые поступления и ежегодное начисление процентов);

• платежи поступают более редко по сравнению с начислением процентов (на­пример, полугодовые поступления и ежеквартальное начисление процентов).

Первая ситуация наиболее прозрачна. Например, если речь идет об аннуитете, удается оценить поток с помощью несложных процедур с привлечением фактор­ных и дисконтирующих множителей. Вторая и третья ситуации уже менее очевид­ны и требуют некоторых усилий. Технику вычислений в упомянутых ситуациях рассмотрим на примерах; при этом предполагается, что финансовые операции осу- ществляются опытными участниками рынка, действующими исходя из очевидного требования максимизации возможного дохода (минимизации возможных затрат). В частности, выражением данной предпосылки является применение, как правило, схемы сложных процентов.

Пример

Периодически в течение 3 лет в банк делается вклад по схеме пренумерандо в сумме 400 тыс. руб. Какая сумма будет на счете к концу операции, если предла­гаемая банком процентная ставка наращения равна 12% годовых? Рассмотреть три ситуации: (1) поступления ежегодные (единовременная сумма 400 тыс. руб. в год вносится на счет в начале каждого года), начисление процентов ежегодное;

2. поступления ежеквартальные (по 100 тыс. руб. в квартал в течение 3 лет), на­числение процентов ежегодное; (3) поступления ежегодные (единовременная сум- ма 400 тыс. руб. в год), начисление процентов ежеквартальное.

Решение

Прежде чем читатель познакомится с результатами расчетов, предлагаем ему попытаться спрогнозировать ожидаемые результаты на качественном уровне, т. е. ответить на вопрос: в какой из ситуаций по окончании операции на счете будет накоплена большая (меньшая) сумма и почему?

Ситуация 1

Это типовой вариант финансовой операции со следующими характеристика­ми: денежный поток представляет собой аннуитет пренумерандо с величиной ан­нуитетного платежа 400 тыс. руб.; число элементов потока равно трем; базовый интервал — год; ставка наращения — 12% (см. рис. 6.15).

Рис. 6.15. Поток пренумерандо при совпадении частот поступления платежей и начисления процентов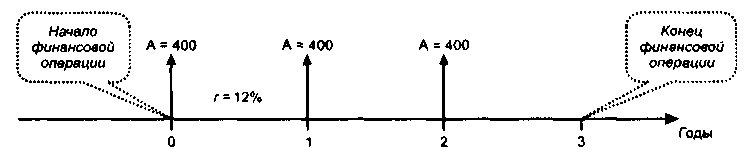

Оценка будущей стоимости данного потока может быть сделана с помощью формулы (6.34):

Ситуация 2

Финансовая операция начинается в момент 0 и заканчивается в момент 12. Характеристики денежного потока таковы: поток представляет собой аннуитет пренумерандо с величиной аннуитетного платежа .4 = 100 тыс. руб.; число эле­ментов потока равно 12; базисный интервал — квартал (см, рис. 6.16),

Рис. 6. 16. Поток пренумерандо при поквартальных взносах и годовом начислении процентов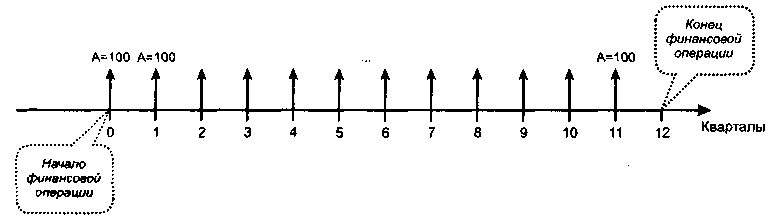

Здесь простейшие типовые формулы оценки будущей стоимости (как в си­туации 1) аннуитета уже не применимы, поскольку начисления процентов осу­ществляются лишь в моменты 4, 8 и 12. Для того чтобы понять логику нараще­ния в этом случае, рассмотрим сепаратно один произвольный год, например пер­вый. Денежный поток будет выглядеть следующим образом (рис. 6.17): (CF_k - Л, k = 1.2,... 12)

Рис. 6.17. Поток пренумерандо в рамках произвольного года, рассматриваемого сепаратно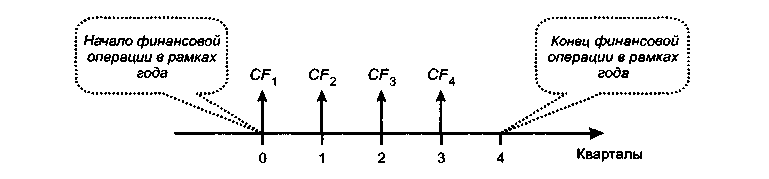

Логика начисления процентов такова. Платеж С Ft, находится в банке один квартал, а потому при единовременном начислении процентов в конце года к нему должна быть применена квартальная ставка. Аналогично в отношении платежей CF3, CF-,, CF, должны применяться соответственно ставка полугодовая, три четверти годовой ставки и годовая ставка. А потому к концу года на счете будет находиться сумма

Подобное имеет место и в отношении других лет, рассматриваемых сепаратно, А потому исходный поток пренумерандо с величиной платежа 100 тыс. руб. и ба­зисным интервалом квартал трансформируется в поток постнумерандо (рис. 6.18)

с тремя аннуитетным к платежами, величиной платежа 430 тыс. руб., ставкой на­ращения 12% и базисным интервалом в 1 год.

Рис. 6.18. Трансформация исходного потока с поквартальной разбивкой взносов в поток постнумерандо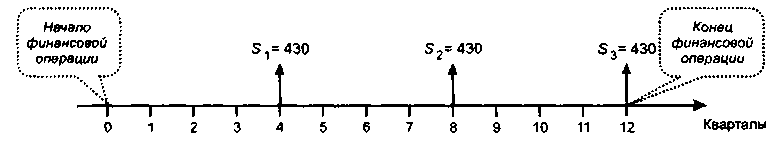

Имеем аннуитет постнумерандо, будущая стоимость которого рассчитывается по формуле (6.30):

Сравнивая результаты расчетов в ситуациях I и 2, можно заметить, что вто­рая накопленная сумма оказалась меньше первой. Приведенный выше разбор счетного алгоритма объясняет причину этого. Разбиение головой суммы на 4 час­ти приводило к тому, что во второй ситуации относительно меньшая сумма в среднем была в распоряжении банка, поэтому естественно, что и меньшая сумма процентов была начислена.

Ситуация 3

Если рассматривать каждый год сепаратно, для расчета суммы, накопленной к концу года на счете, надо воспользоваться формулой (6.10). В разд. 6.3 было по­казано, что номинальной ставке с внутрнгодовыми начислениями соответствует эффективная ставка, исчисляемая по формуле (6.18) и предусматривающая одно­кратное начисление

Таким образом, оцениваемый денежный поток представляет собой аннуитет пре­нумерандо с тремя аннуитетными платежами, величиной платежа А = 400 тыс. руб., базисным интервалом в 1 год и ставкой наращения г_е ~ 12,55% (рис. 6.19).

Рис. 6.19. Исходный поток при переходе к эффективной процентной ставке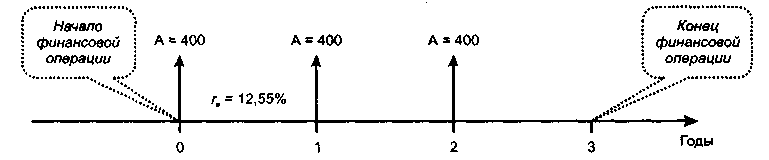

Для расчета итоговой суммы, накопленной на счете к концу 3-летнего перио­да, воспользуемся формулами (6.34) и (6.31):

Сравнивая сумму, исчисленную в данной ситуации, с предыдущими расчет­ными суммами, видим, что и здесь получили вполне оправданный результат. Си­туация 3 является самой выгодной с позиции накопления денежных средств, а причина выгодности в большей частоте начисления процентов.

В теории финансовых вычислений разработаны унифицированные формулы, позволяющие упростить расчеты в случаях, когда имеет место несовпадение мо­ментов поступления платежей (т. е. элементов денежного потока) и начисления процентов. Для потоков постнумерандо и пренумерандо в случае применения схе­мы сложных процентов эти формулы имеют соответственно вид

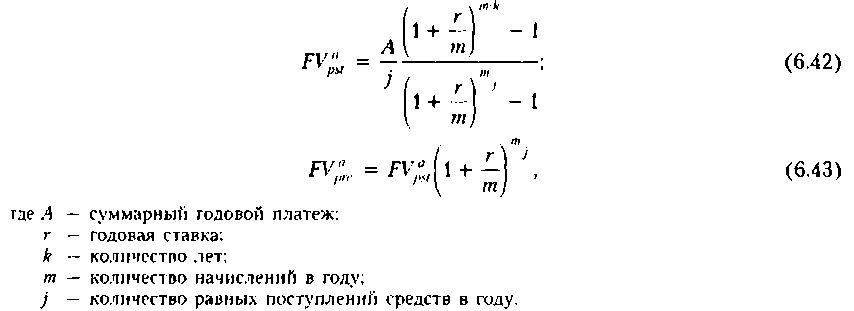
Предлагаем читателю самостоятельно сделать расчеты с помощью формул (6.42) и (6.43) для данных только что рассмотренного примера (возможные незна­чительные расхождения объясняются приблизительностью значений факторных множителей из финансовых таблиц).

Несмотря на наличие специальных формул, мы посчитали целесообразным в подробностях рассмотреть логику и технику расчетов в примере. Причина в том, что нередко счетные формулы применяются механически, необдуманно. Подобное может приводить к заведомо неверным результатам. По нашему глубокому убеж­дению, финансовый аналитик должен уметь прогнозировать на качественном уровне исчисляемые результаты. Дело в том, что нередко для принятия решений финансового характера собственно цифра (число) не столь уж важна (например, с позиции точности). Важна тенденция, важно понимать логику операции, дейст­вия, алгоритма и заранее (если это возможно) делать суждение о том, что данная операция более выгодна, нежели альтернативная. Если хочется знать, насколько она выгодна, требуется более или менее точный расчет.

Что касается сути проблемы соотношения частот поступления платежей и на­числения процентов, проанализированной в примере, то несложно сделать очевид­ное обобщение: целесообразно выровнять продолжительность периода начисления процентов и периода поступления платежа. Для понимания логики процентных начислений можно, например, руководствоваться следующими правилами:

• если элементы денежного потока поступают более часто по сравнению с начис­лением процентов, рекомендуется исходный поток привести к условному пото­ку, в котором момент поступления очередного платежа будет совпадать с мо­ментом начисления процентов в исходном потоке (иными словами, необходимо промежуточные платежи в рамках одного интервала между смежными момен­тами начисления процентов свести к очередному моменту начисления процен­тов), и далее воспользоваться стандартными формулами оценки аннуитета;

• если проценты начисляются более часто по сравнению с поступлением ан­нуитетных платежей, можно воспользоваться формулами оценки аннуитета, в которых номинальная процентная ставка заменена на соответствующую эф­фективную ставку.

В заключение главы отметим, что приводимые в книге обозначения фактор­ных множителей FM\(r, п), FM2(r, и), FM3(r, л), FA/4 (г, п) являются условными; в англоязычной и переводной литературе широко распространены следующие обо­значения (в порядке соответствия); FVIF(r, п), PVIF(r, я), FVIFA(r, п), PVlFA(r, п), представляющие собой аббревиатуры соответствующих англоязычных наименова­ний этих множителей: Future-Value Interest Factor, Future-Value Interest Factor for an Annuity, Present-Value Interest Factor, Present-Value Interest Factor for an Annuity.

Заканчивая изложение материалов главы, еще раз сформулируем ключевые моменты, которые необходимо иметь в виду при проведении финансовых и ком­мерческих расчетов:

• проводя количественное обоснование той или иной финансовой операции, необходимо контролировать соответствие процентной ставки и продолжи­тельности базисного периода;

• необходимо отдавать себе отчет в том, в каких единицах (процент или доля единицы) следует включать в расчет данные о процентных ставках;

• реальная эффективность финансовой сделки характеризуется эффективной годовой процентной ставкой, однако во многих финансовых контрактах речь чаще всего идет о номинальной ставке, которая в большинстве случаев отли­чается от эффективной;

• заключая контракт, целесообразно уточнять, о какой ставке (процентной, учетной, эффективной и др.) идет речь, или по крайней мере отдавать себе отчет в этом;

• ни одна из схем начисления процентов не является универсальной и пригод­ной на все случаи жизни, т. е. нельзя определенно и однозначно отдавать приоритет той или иной схеме. Все зависит от конкретных обстоятельств;

• при анализе денежных потоков в большинстве случаев его элементы не мо­гут быть просуммированы непосредственно. Должна быть учтена временная компонента;

• начало денежного потока и момент, на который делается оценка или к кото­рому приводится денежный поток (потоки), могут не совпадать;

• приведение денежных потоков в сравнительном анализе, в принципе, может делаться по отношению к любому моменту времени, однако, как правило, выбирается либо начало, либо конец периода действия одного из денежных потоков.

Наконец, хотелось бы особо подчеркнуть, что многие из рассмотренных алго­ритмов финансовой математики не являются чем-то принципиально новым для отечественной науки и практики. Любопытному читателю можно порекомендо­вать обратиться к трудам профессора Н. С. Лунского, плодотворно работавшего в области теории и практики коммерческих и финансовых вычислений в первой четверти XX в. Лунского по праву можно считать одним из родоначальников фи­нансового анализа в России (см. Библиографию).

Материалы для самостоятельной работы

Дайте определение следующим ключевым понятиям: наращение, дисконтирование, процентная ставка, учетная ставка, правило 72-х, дискретное начисление, непрерывное на­числение, сила роста, эффективная ставка, будущая стоимость, дисконтированная стои­мость, мультиплицирующий множитель, дисконтирующий множитель, поток пренумерандо, поток постнумерандо, аннуитет, метод депозитной книжки.

Вопросы для обсуждения

1. Зачем надо учитывать временную ценность денежных средств?

2. Как соотносятся между собой процентная и учетная ставки?

3. В чем состоит принципиальная разница между схемами простых и сложных про­центов?

4. Какой тип наращения предпочтителен при хранении денег в банке?

5. В чем разница между точным и обыкновенным процентами?

6. Вы располагаете данными о сумме, которую можно получить через 5 лет, и хотите продать этот контракт немедленно. Какими расчетными формулами целесообразно воспользоваться и почему?

7. Какое начисление процентов — более или менее частое — и при каких условиях бо­лее выгодно?

8. Какая схема и почему более выгодна при начислении процентов за дробное число лет?

9. В чем смысл эффективной годовой процентной ставки? От чего зависит ее величина?

10. Какие виды денежных потоков вы знаете?

11. Что такое финансовые таблицы и как ими пользоваться?

12. Могут ли совпадать будущая и дисконтированная стоимости? Если да, то при каких условиях?

13. Поясните правило 72-х.

14. В чем смысл прямой и обратной задач оценки денежного потока?

15. Зависят ли данные в финансовых таблицах от вида денежного потока?

16. Связаны ли между собой значения будущей стоимости потоков пренумерандо и по­стнумерандо?

17. Поясните метод депозитной книжки.