2. Метод депозитной книжки

Можно дать иную интерпретацию расчета дисконтированной стоимости ан­нуитета с помощью метода депозитной книжки, логика которого такова. Сумма, положенная на депозит, приносит доход в виде процентов. При снятии с депозита некоторой суммы базовая величина, с которой начисляются проценты, уменьшает­ся. Как раз эта ситуация имеет место в случае с аннуитетом. Текущая стоимость аннуитета — это величина депозита с общей суммой причитающихся процентов, ежегодно уменьшающаяся на равные суммы. Эта сумма годового платежа включа­ет начисленные за очередной период проценты, а также некоторую часть основной суммы долга. Таким образом, погашение исходного долга осуществляется посте­пенно, в течение всего срока действия аннуитета. Структура годового платежа по­стоянно меняется. В начальные периоды в нем преобладают начисленные за оче­редной период проценты; с течением времени доля процентных платежей постоян­но уменьшается и повышается доля погашаемой части основного долга. Логику и счетные процедуры метода рассмотрим на примере.

Пример

В банке получена ссуда на 5 лет в сумме 20 ООО долл. под 13% годовых, на­числяемых по схеме сложных процентов на непогашенный остаток. Возвращать надо равными суммами в конце каждого года. Требуется определить величину го­дового платежа.

Решение

Если обозначить за А величину искомого годового платежа, то данный фи­нансовый контракт можно представить в виде следующей схемы (рис. 6.13).

Рис. 6.13. Схема к методу депозитной книжки

Заметим прежде всего, что на рис. 6.13 фактически изображены два денежных потока: первый связан с оттоком денежных средств и состоит из одного элемента, равного величине инвестиции в сумме 20 тыс. долл.; второй связан с притоками денежных средств и представлен аннуитетом постнумерандо (рассуждения приве-дены с позиции банка). Иными словами, стрелка, демонстрирующая отток денеж­ных средств, ие является элементом денежного потока, демонстрирующего посту­пления, т. е. сформулированное выше правило о совпадении числа стрелок н чис­ла базисных интервалов в контексте одного потока здесь выполнено.

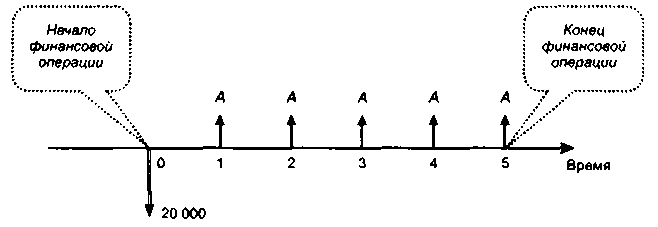
Для лучшего понимания логики метода депозитной книжки целесообразно рассуждать с позиции кредитора. Для банка данный контракт представляет со­бой инвестицию в размере 20 ООО долл., т. е. отток денежных средств, что и пока­зано на схеме. В дальнейшем в течение 5 лет банк будет ежегодно получать в конце года сумму А, причем каждый годовой платеж будет включать проценты за истекший год и часть основной суммы долга. Так, поскольку в течение перво­го года заемщик пользовался кредитом в размере 20 ООО долл., то платеж, кото­рый будет сделан в конце этого года, состоит из двух частей: процентов за год в сумме 2600 долл. (13% от 20 000 долл.) и погашаемой части долга в сумме (А - 2600) долл. В следующем году расчет будет повторен при условии, что раз­мер кредита, которым пользуется заемщик, составит уже меньшую сумму по сравнению с первым годом, а именно (20000 — А + 2600)долл. Отсюда видно, что с течением времени сумма уплачиваемых процентов снижается, а доля платежа в счет погашения долга возрастает. Из схемы на рис, 6.13 видно, что мы имеем дело с аннуитетом постнумерандо, о котором известна его текущая стоимость, процентная ставка н продолжительность действия. Поэтому для нахождения ве­личины годового платежа А можно воспользоваться формулой (6.35):

Динамика платежей показана в таблице. Отметим, что данные в ходе вычис­лений округлялись, поэтому величина процентов в последней строке найдена ба­лансовым методом.

Метод депозитной книжки

Данная таблица позволяет ответить на целый ряд дополнительных вопросов, представляющих определенный интерес для прогнозирования денежных потоков. В частности, можно рассчитать общую сумму процентных платежей, величину процентного платежа в k-м периоде, долю кредита, погашенную в первые k лет, н т. п.