2. Оценка потока пренумерандо

Логика оценки денежного потока в этом случае аналогична вышеописанной. Некоторое расхождение в вычислительных формулах объясняется сдвигом эле­ментов потока к началу соответствующих базисных подынтервалов. Для прямой задачи схема наращения приведена на рис. 6.10.

Рис. 6.10. Схема наращения элементов денежного потока пренумерандо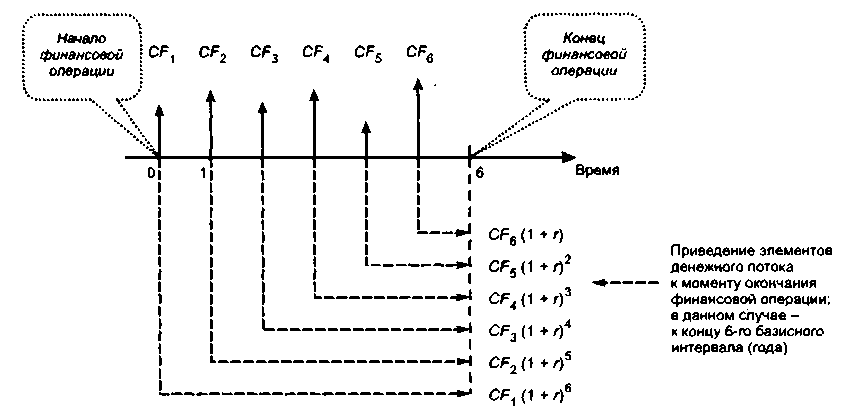

Сравнивая рис. 6.8 и 6.10, несложно понять, что различие между потоками пост- и пренумерандо заключается лишь в том, что поток пренумерандо сдвинут влево на один интервал. Это приводит к дополнительному однократному начисле­нию процентов, а формула расчета будущей стоимости потока пренумерандо будет иметь вид (это видно из рис. 6.10)

Отсюда с очевидностью следует, что в общем случае

Итак, взаимосвязь между стоимостными оценками потоков пост- и пренуме- рандо выражается следующей формулой:

Иными словами, схема потока пренумерандо более выгодна для накопления денежных средств, нежели схема постнумерандо.

Для обратной задачи схема дисконтирования, т. е. приведения всех элементов исходного потока в точку 0, может быть представлена рис. 6.11.

Рис. 6.11. Схема дисконтирования элементов денежного потока пренумерандо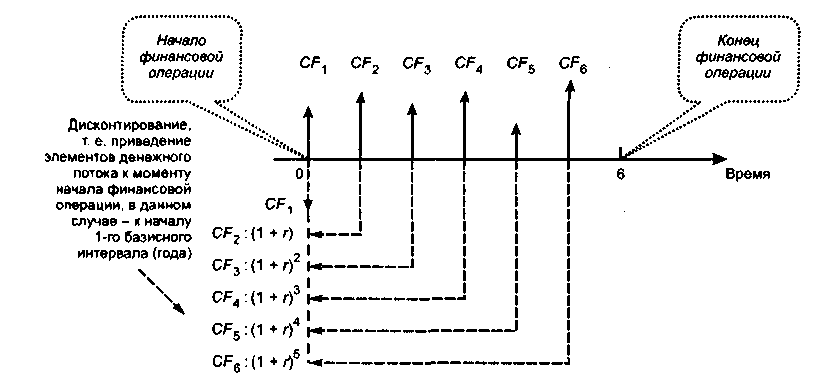

Сравнивая рис. 6.11 и 6.9, вновь видим, что различие между потоками пост- и пренумерандо заключается лишь в том, что поток пренумерандо сдвинут влево на один интервал. Это приводит к уменьшению делителя на величину (1 + г). Дейст­вительно, элемент CF\ уже находится в начале 1 -го базисного интервала, т. е. в точ­ке 0, а потому дисконтирование не требуется; элемент CF^ отдален от точки 0 на один интервал, а потому его дисконтирование сводится к делению на (1 + г), и т. д. После приведения всех элементов потока в точку 0 их можно просуммировать.

Таким образом, в общем виде формула для исчисления дисконтированной стоимости потока поенумеоанло имеет следующее поелставление:

Иными словами, как и в случае с будущей стоимостью, дисконтированная стоимость потока пренумерандо превышает дисконтированную стоимость соответ­ствующего потока постнумерандо на величину (1 -I- г). Так, если в предыдущем примере предположить, что исходный поток представляет собой поток пренуме­рандо, то его дисконтированная стоимость будет равна

4. Оценка аннуитетов

Одним из ключевых понятий в финансовых и коммерческих расчетах является понятие аннуитета. Логика, заложенная в схему аннуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестици­онных проектов, а также в анализе аренды.

1. Оценка срочного аннуитета

Аннуитет (иногда в литературе используются термины «рента», «финансовая рента») представляет собой частный случай денежного потока. Известны два под­хода к его определению. Согласно первому подходу аннуитет представляет собой однонаправленный денежный поток, элементы которого имеют место через рав­ные временные интервалы. Второй подход накладывает дополнительное ограниче­ние: элементы денежного потока одинаковы по величине. В дальнейшем изложе­нии материала мы будем придерживаться именно второго подхода.

Любой элемент денежного потока называется членом аннуитета (членом рен­ты), а величина постоянного временного интервала между двумя его последова­тельными элементами называется периодом аннуитета (периодом ренты). Если каждый элемент аннуитета имеет место в конце соответствующего периода, ан­нуитет называется аннуитетом постнумерандо (Ordinary Annuity); если в начале периода — аннуитетом пренумерандо (Annuity Due). Аннуитет, все элементы ко­торого равны между собой, называется постоянным; если равенства нет, аннуитет носит название переменного.

Пример аннуитета пренумерандо: накопление денег на банковском счете, когда вклады делаются, например, в начале каждого месяца. Пример аннуитета постну­мерандо: регулярное получение процентов по ценной бумаге (по вкладу) по ито­гам очередного месяца.

Если число равных временных интервалов ограничено, аннуитет называет­ся срочным; в противном случае аннуитет носит название бессрочного. Для срочного аннуитета: CF_{ = CF₂ = ... = CF„ = А. Графическое представление сроч­ного аннуитета пост- и пренумерандо приведено на рис. 6.12. Вновь обращаем внимание читателя на то, что в обоих случаях финансовая операция, описывае­мая аннуитетом, начинается в точке 0 и заканчивается в точке п (грубо говоря, делая графические построения и проводя расчеты, всегда надо помнить о нехит­ром правиле: число стрелок и количество базисных интервалов должно совпа­дать).

Примером срочного аннуитета постнумерандо могут служить регулярно посту­пающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истече­нии очередного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления суммы для крупной покупки.

Исторически вначале рассматривались ежегодные денежные поступления (ба­зисный период принимался равным одному году), что и послужило основой для поименования потока аннуитетом («год» на латинском языке — anno). В дальней­шем в качестве периода стал выступать любой промежуток времени при сохране­нии прежнего названия.

Рис. 6.12. Виды срочных аннуитетов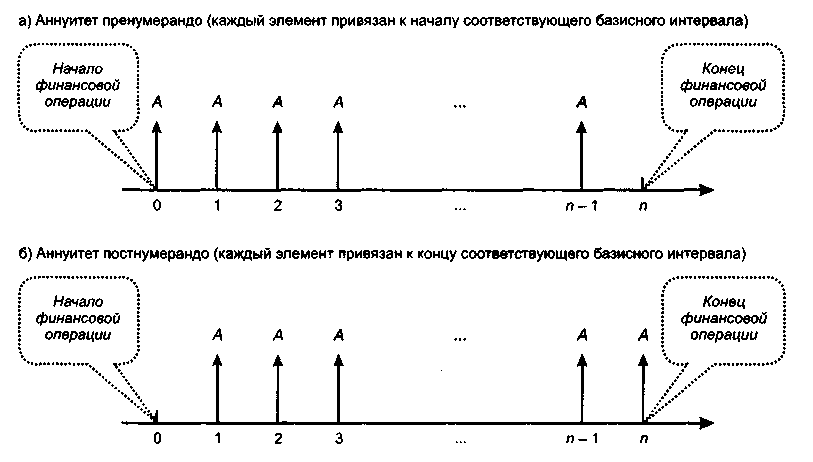

Как и в случае с нетипизированным денежным потоком, в отношении аннуите­тов имеют место прямая и обратная задача. Специфика аннуитета (равенство де­нежных поступлений) позволяет вывести стандартизованные формулы, сущест­венно упрощающие счетные процедуры. Логика рассуждений точно такова, как и в разд. 6.6.

Будущая стоимость аннуитета постнумерандо (т. е. денежного потока постну­мерандо с равными элементами) представляет собой сумму наращенных элемен­тов потока, исчисляемую в предположении, что: (а) все элементы одинаковы,

(б) каждый элемент потока начинается в конце соответствующего базисного ин­тервала и (в) наращение осуществляется по схеме сложных процентов с использо­ванием заданной процентной ставки г.

Для демонстрации логики расчета можно воспользоваться графиком на рис. 6.8 в предположении, что CF_h = ,4 = const, а горизонт планирования равен п.

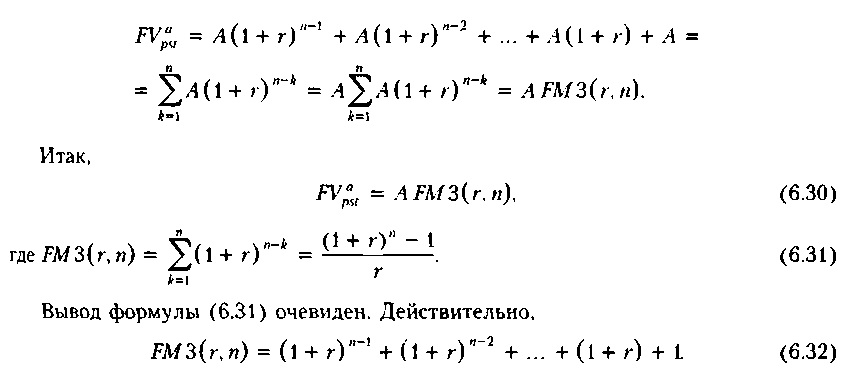
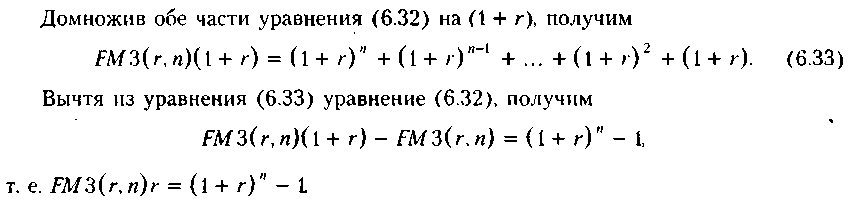
Отсюда и следует формула (6.31).

Экономический смысл FM3{r, и), называемого мультиплицирующим множите­лем для аннуитета, заключается в следующем. Он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что проводится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель FM3(r,n) часто используется в финансовых вы­числениях. Его значения зависят лишь от процентной ставки г и срока п действия аннуитета, причем с увеличением каждого из этих параметров величина FM3(r, п) возрастает. Значения множителя для различных сочетаний г и и можно табулиро­вать (см. Приложение 3).

Из (6.30) следует, что FM3(r, п) показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления А. В связи с этим множитель FM3(r. п) называют также коэффициентом аккумуляции вкладов.

Будущая стоимость аннуитета пренумерандо (т. е. денежного потока пренуме­рандо с равными элементами) представляет собой сумму наращенных элементов потока, исчисляемую в предположении, что: (а) все элементы одинаковы, (б) каж­дый элемент потока начинается в начале соответствующего базисного интервала и

(в) наращение осуществляется по схеме сложных процентов с использованием за­данной процентной ставки г.

Для демонстрации логики расчета можно воспользоваться графиком на рис. 6.10 в предположении, что CF_k — А = const. Как было показано в разд. 6.6, значения будущей стоимости потоков пренумерандо и постнумерандо отличаются на множитель (1 + г), т. е. будущая стоимость денежного потока пренумерандо рас* считывается по формуле

Дисконтированная стоимость аннуитета постнумерандо (Present Value of Ordinary Annuity) (т. e. денежного потока постнумерандо с равными элементами) представляет собой сумму приведенных к началу финансовой операции элементов потока, исчисляемую в предположении, что: (а) все элементы одинаковы, (б) каж­дый элемент потока начинается в конце соответствующего базисного интервала и

(в) дисконтирование осуществляется по схеме сложных процентов с использова­нием заданной процентной ставки г.

Для демонстрации логики расчета можно воспользоваться графиком на рис. 6.9 в предположении, что CF_k = А = const, а горизонт планирования равен п.

Отсюда и следует формула (6.36).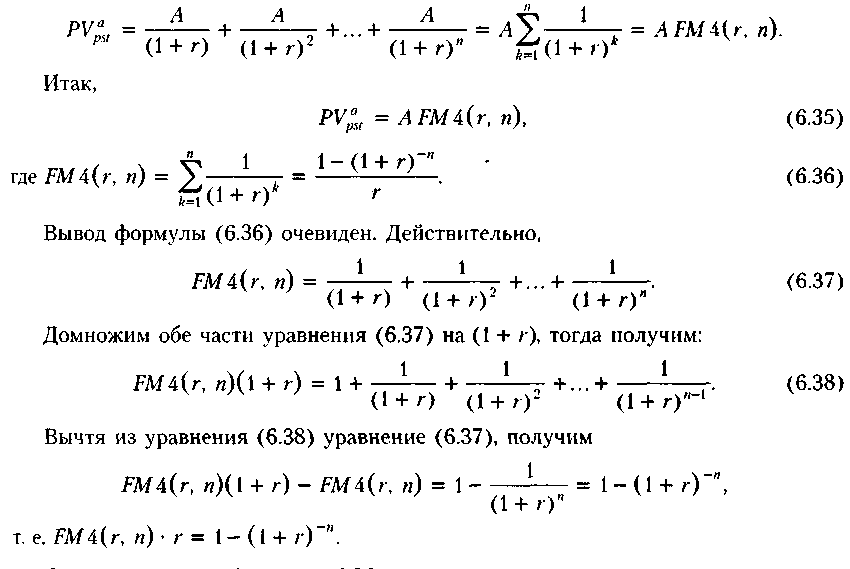

Экономический смысл FMA(r, п), называемого дисконтирующим множите­лем для аннуитета, заключается в следующем. Он показывает, чему равна, с по­зиции текущего момента (т. е. момента, на который осуществляется дисконтиро­вание), суммарная величина срочного аннуитета в одну денежную единицу (на­пример, один рубль), продолжающихся п равных базисных периодов с заданной процентной ставкой г. Множитель FMA(r, п) часто используется в финансовых вычислениях, и поскольку его значения в общем виде зависят лишь от г и п, они табулированы. Благодаря этому существенно упрощаются расчеты (см. Прило­жение 3).

При одном денежном поступлении и, следовательно,

Поскольку FM4(0, п) = и, то мри г = 0 справедливо PV“_st = п - А. Кстати, отсюда следует очевидное и с финансовой точки зрения утверждение:

Дисконтирующий множитель FMA (г, к) полезно интерпретировать как вели­чину капитала, поместив который в банк под сложную процентную ставку г, мож­но обеспечить регулярные выплаты в размере одной денежной единицы в течение п периодов (выплаты проводятся в конце каждого периода).

Дисконтированная стоимость аннуитета пренумерандо (Present Value of Annuity Due) (т. e. денежного потока пренумерандо с равными элементами) пред­ставляет собой сумму дисконтированных элементов потока, исчисляемую в пред­положении, что: (а) все элементы одинаковы, (б) каждый элемент потока начина­ется в начале соответствующего базисного интервала и (в) дисконтирование осу­ществляется по схеме сложных процентов с использованием заданной процентной ставки г.

Для демонстрации логики расчета можно воспользоваться графиком на рис. 6.11 в предположении, что CF_k = А = const, а горизонт планирования равен п. Вновь вспомним о том, что значения дисконтированной стоимости потоков прену­мерандо и постнумерандо отличаются на множитель (1 + г), т. е. дисконтированная стоимость денежного потока пренумерандо рассчитывается по формуле

Общие замечания. Из приведенных в данном разделе формул видно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке — постнумерандо или пренумерандо. Дело в том, что содержание любой базовой финансовой таблицы инвариантно к этому фактору. Однако при примене­нии расчетных формул или финансовых таблиц необходимо строго следить за схе­мой поступления денежных платежей, поскольку величина будущей или дискон­тированной стоимости аннуитета зависит от его вида.

Многие практические задачи могут быть решены разными способами, в зави­симости от того, какой денежный поток выделен аналитиком. Рассмотрим пример.

Пример

Вам предложено инвестировать 100 тыс. руб. на срок 5 лет при условии воз­врата этой суммы частями (ежегодно по 20 тыс. руб.). По истечении 5 лет выпла­чивается дополнительное вознаграждение в размере 30 тыс. руб. Принимать ли это предложение, если можно безопасно депонировать деньги в банк из расчета 12% годовых?