4. Оценка денежного потока с неравными поступлениями

Ситуация, когда денежные поступления по годам варьируют, является наибо­лее распространенной. Общая постановка задачи в этом случае такова.

Пусть CF_{, CF₂, ..., CF„ — денежный поток; г — ставка дисконтирования. По­ток, все элементы которого с помощью дисконтирующих множителей приведены к одному моменту времени, а именно — к настоящему моменту времени, называется дисконтированным (иногда используется термин «приведенный»). Требуется найти стоимость данного денежного потока с позиции будущего и с позиции настоящего.

1. Оценка потока постнумерандо

Прямая задача предполагает оценку с позиции будущего, т. е. на конец периода и, когда реализуется схема наращения, которую можно представить следующим образом (рис, 6.8).

Рис. 6.8. Схема наращения элементов денежного потока постнумерандо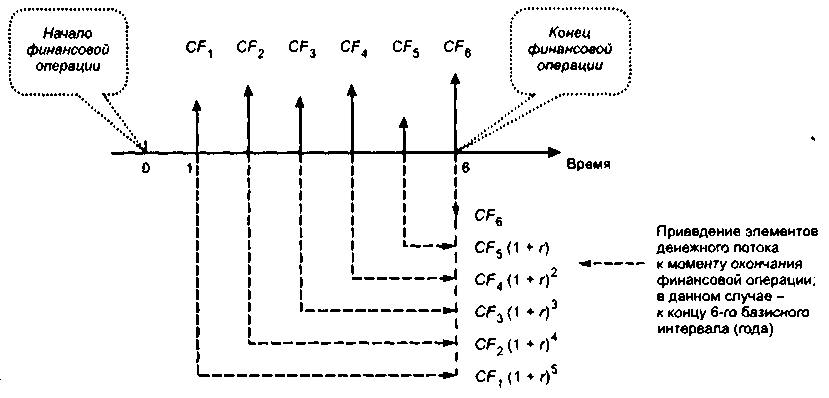

Представим себе, что множество {CF_k}, к — 1, 2, .... п — это совокупность пе­риодических денежных взносов в банк на депозит. Какая сумма будет в концу данной операции? Предполагается, что инвестор безусловно знаком с понятием временной ценности денег и, кроме того, хотел бы получить некоторое вознаграж­дение за отвлечение своих собственных средств. Простое суммирование элементов потока {CFj} невозможно, поскольку они находятся в разных временных интерва­лах, что обусловливает их несопоставимость из-за временной ценности денег. Эта несопоставимость устраняется с помощью наращения по схеме сложных процен­тов. Поскольку имеем поток постнумерандо, это означает, что финансовая опера- ция заканчивается в конце последнего базисного периода (на рис. 6.8 это конец 6-го периода). Элемент CF& уже находится в этой точке, поэтому наращения не требуется; элемент CF$ находится в конце 5-го периода, а потому по истечении 6-го периода на эту сумму будут начислены проценты по ставке г. Сумма CF_A тре­бует двукратного начисления, и т.д. После приведения всех элементов потока в точку 6 их можно просуммировать.

Таким образом, общая формула для исчисления будущей стоимости потока постнумерандо имеет следующий вид:

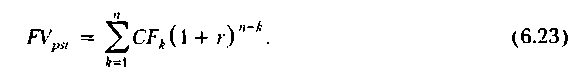
Обратная задача подразумевает оценку с позиции текущего момента, т. е. на начало периода 1. В этом случае реализуется схема дисконтирования, т. е. все эле­менты ожидаемого денежного потока сводятся к началу финансовой операции — в точку 0. Схема дисконтирования для исходного потока постнумерандо имеет сле­дующий вид (рис. 6.9). Заметим, что в общем случае равенство элементов потока не предполагается, а логика рассуждений такова.

Пусть имеем исходный денежный поток CF_V СР₂, ..., CF„. Представим себе, что это совокупность регулярных доходов по ценной бумаге, которую инвестору предлагают купить. Инвестор хочет понять, сколько он готов заплатить за воз­можность обладания данным потоком. Речь идет о грамотном участнике рынка, который знаком с понятием временной ценности денег и, кроме того, хотел бы по­лучить приемлемое вознаграждение за единовременное отвлечение своих собст­венных средств, неизбежное при покупке ценной бумаги. Очевидно, что напраши­вающееся простое суммирование элементов потока CFk невозможно, поскольку они находятся в разных временных интервалах, что обусловливает их несопоста­вимость (в частности, из-за временной ценности денег). Эта несопоставимость устраняется с помощью дисконтирования по схеме сложных процентов.

Рис. 6.9. Схема дисконтирования элементов денежного потока постнумерандо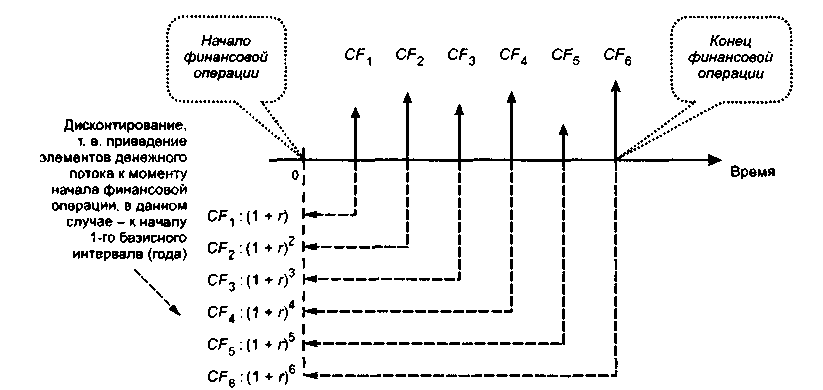

Финансовая операция подразделяется на п базисных периодов, к концу каждо­го из которых привязан очередной платеж CF* (на рис. 6.9 это 6 периодов). Расчет дисконтированной стоимости данного потока сводится к приведению каждого его элемента к началу финансовой операции, т. е. в точку 0, т. е. к делению на множи­тель (1 + г) в соответствующей степени.

Элемент CF\ отдален от точки приведения на один интервал, потому он делит­ся на (1 + г); элемент CF-, отдален двумя интервалами, а потому делится на (1 + г)², и т. д. После приведения всех элементов потока в точку 0 их можно про­суммировать.

Таким образом, общая формула для исчисления дисконтированной стоимости потока постнумерандо имеет следующий вид:

)

Если использовать дисконтирующий множитель для единичного платежа, то формулу (6.24) можно переписать в следующем виде:

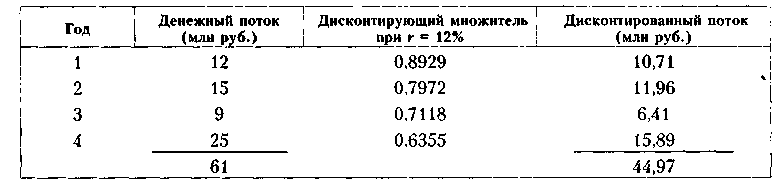
Пример

Рассчитать дисконтированную стоимость денежного потока постнумерандо (млн руб.): 12, 15, 9, 25, если ставка дисконтирования г = 12%.

Решение

Результаты расчетов приведены в таблице.

Как видим, чем дальше от начала финансовой операции отстоит элемент де­нежного потока, тем более осторожна его оценка. Все элементы дисконтированно­го потока уже приведены в точку 0, а потому их можно просуммировать, а полу­ченную сумму 44,97 млн руб. можно сравнивать, например, с запрашиваемой сум­мой инвестиции.