Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.
Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной
Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны)
Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ).
Признаки равенства треугольников.
Треугольники равны, если у них соответственно равны:
a) двум сторонам и уголу между ними;
b) по стороне и двум прилежащим к ней углам
c) трем сторонам.
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. c 2 = a 2 + b 2 .
Часть плоскости, ограниченная окружностью, называется кругом.
Касательная. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания
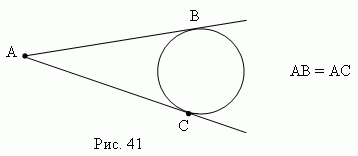
2) Из точки, лежащей вне круга, можно провести две касательные к одной и той же окружности; их отрезки равны ( рис.41 ).
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.42 ).
Сектор – это часть круга, ограниченная дугой AmB и двумя радиусами OA и OB, проведенными к концам этой дуги ( рис.43 ).
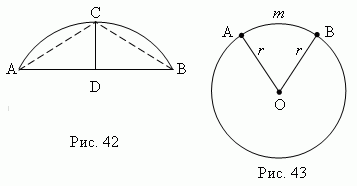
Параллелограмм ( ABCD, рис.32 ) – это четырёхугольник, противоположные стороны которого попарно параллельны
Свойства параллелограмма.
1. Противоположные стороны параллелограмма равны ( AB = CD, AD = BC ).
2.
Противоположные углы параллелограмма
равны (
![]() A
=
C,
B
=
D
).
A
=
C,
B
=
D
).
3. Диагонали параллелограмма делятся в точке их пересечения пополам ( AO = OC, BO = OD ).
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон: AC² + BD² = AB² + BC² + CD² + AD² .

Прямоугольник.
Если один из углов параллелограмма прямой, то все остальные углы также прямые. Такой параллелограмм называется прямоугольником ( рис.33 ) .
сновные свойства прямоугольника.
Стороны прямоугольника являются одновременно его высотами.
Диагонали прямоугольника равны: AC = BD.
Квадрат диагонали прямоугольника равен сумме квадратов его сторон
AC 2 = AD 2 + DC 2 .
Ромб.
Если все стороны параллелограмма
равны, то этот параллелограмм называется
ромбом ( рис.34 ) . Диагонали ромба
взаимно перпендикулярны (
AC
![]() BD
) и делят их углы пополам (
DCA
=
BCA,
ABD
=
CBD
и т.д. ).
BD
) и делят их углы пополам (
DCA
=
BCA,
ABD
=
CBD
и т.д. ).
Квадрат – это параллелограмм с прямыми углами и равными сторонами ( рис.35 ). Квадрат является частным случаем прямоугольника и ромба одновременно; поэтому он обладает всеми их вышеперечисленными свойствами.
Трапеция - это четырёхугольник, у которого две противоположные стороны параллельны ( рис.36 ).
Средняя линия треугольника – это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине его основания и параллельна ему
(с 9 кл) Вписанным в круг называется многоугольник, вершины которого расположены на окружности ( рис.54 )
Описанным около круга называется многоугольник, стороны которого являются касательными к окружности ( рис.55 ).
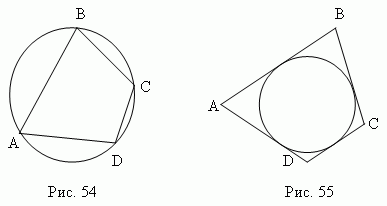
окружность, проходящая через вершины многоугольника ( рис.54 ), называется описанной около многоугольника;
окружность, для которой стороны многоугольника являются касательными ( рис.55 ), называется вписанной в многоугольник.
67)(с 9 кл) Правильный многоугольник – это многоугольник с равными сторонами и углами.
68)( с 10 кл) Двугранный угол. Фигура, образованная двумя полуплоскостями Q и R, проходящими через одну и ту же прямую MN ( рис.74 ), называется двугранным углом.
Прямая MN называется ребром двугранного угла; полуплоскости Q и R – его гранями. Плоскость P, перпендикулярная к ребру MN, даёт в её пересечении с полуплоскостями Q и R угол AOB.
Угол AOB называется линейным углом двугранного угла.
Двугранный угол измеряется своим линейным углом.

69) Углы между плоскостями.
Две плоскости называются перпендикулярными, если они образуют прямой угол.
Угол между двумя параллельными плоскостями принимается равным нулю.