Загальні вимоги до математичних моделей.
Адекватність. Модель вважається адекватною, якщо відбиває задані властивості об'єкта з прийнятною точністю. Точність визначається як ступінь збігу значень вихідних параметрів моделі й об'єкта.
Універсальність. Якщо адекватність характеризується положенням і розмірами ОА, то універсальність моделі визначається числом і складом зовнішніх і вихідних параметрів, що враховуються в моделі.
Економічність. Вона характеризується витратами обчислювальних ресурсів для її реалізації, що включають витрати машинного часу і пам'яті .
Інформативність.
Адекватність моделі. Критерії адекватності.
Відповідність моделі типовим відомим випадкам
Правильність результатів при граничних значення впливових величин.
Зменшення методичної похибки при врахувнні додаткових факторів(Якщо вона збільшилась – модель неадекватна).
Методичні похибки моделювання.
Характеристики моделей – Адекватність, Складність, Універсальність, Точність (х-ся похибками: обчислювальні, апроксимації, невизначеність даних, методичні – виникають внаслідок нехтування важливимим факторами)
Чутливість, складність, універсальність моделі.
Чутливість моделі – відображення залежності вихідних значень від конкретних вхідних впливів.
Складність моделі – це к-сть зв’язків та елементів, ступінь розрядності(структ. моделі); це вхідні змінні, вихідні змінні, к-сть операцій(функт. моделі); це к-сть даних, к-сть параметрів цих даних і к-сть зв’язків цих даних(інформ. моделі).
Універсальність – визначається потужністю множини об’єктів, що описуються цією моделлю.
Схеми як структурні моделі.
Описують склад системи та зв’язки між елементами.
Основні типи схем: структурні, функціональні, принципові, схеми з’єднувань, загальні, розташування, програм, даних, взаємодії.
Структурні моделі найчастіше зображуються у вигляді графів.
19-20) Графи і графові моделі. Види графів
Граф – це наочне подання елементів системи і зв’язків між ними.
Зв’язки між вершинами бувають двосторонніми і односторонніми. Односторонні зв»язки познач. <- і називаються дугами. Граф в якому є хоч одна дуга наз. Орієнтованим, в якому всі зв’язки двохсторонні – неорієнтованими.
Графи можуть бути зв’язаними і незв’язаними.
Зв’язаний граф – це такий, у якому між кожною парою вершин існує неперервна послідовність вершин і ребер яка дозволяє «пройти» від одної вершини до другої. Ця послідовність вершин і ребер наз. шляхом. Якщо існує така пара вершин між якими немає шляху – граф незв’язний
Характерні частини графа (підграфи).
При аналізі графів складну систему розкладаємо на частини. Підграфи в яких ребра не перетинаються називаються планарними. Шлях у графів в якому поч.. вершина співпадає з кінцевою наз. – циклом.
Цикл який проходить через усі вершини графа по одному разу називається Гамільтона, а цикл який проходить через усі ребра графи називається Ейлера. Підграф без циклів називається деревом. Дерево графа яке містить усі вершини наз. кістяковим деревом.
Граф описується за допомогою матриць. Матриця інциденції показує зв’язок між вершинами та ребрами.
Матриця суміжності – ц квадратна матриця яка відображає зв’язок між вершинами.
Для зважених графів використовується матриця вагів.
21- 22) способи формалізації структурних моделей. Операції над графами.
Оскільки граф як формальний опис структурної моделі є сукупністю двох множин,то операції над структурними моделями, як операції над відповідними вершинами.
1) Операція вилучення ребра 2) операція вилучення вершини 3) операція введення ребра
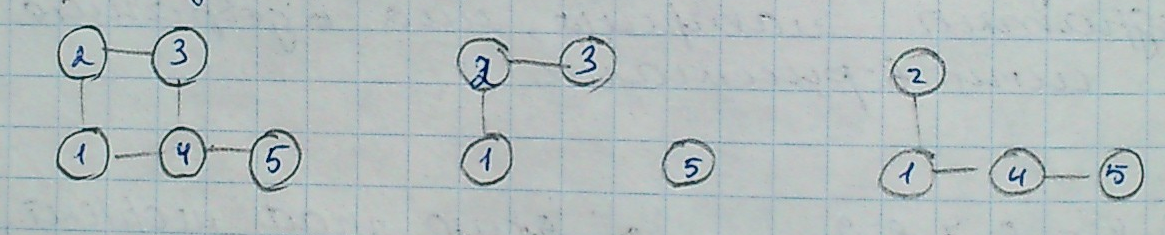
4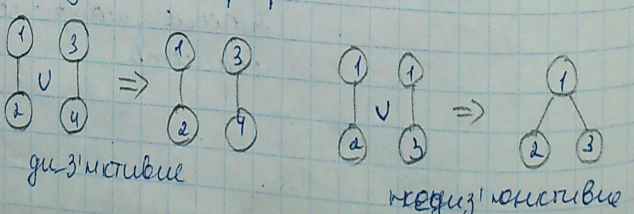
)
Операція введення вершини в ребрах
5) операція об’єднання графів
4) Операція об’єднання графів
6) добуток графів 7) Операція злиття вершин 8) Роздвоєння вершин
9) Операція з’єднання графів (на відміну від опер. об’єднання графів, з’єднання – не однозначне (ми додаємо ребра)).
10)доповнення графів.
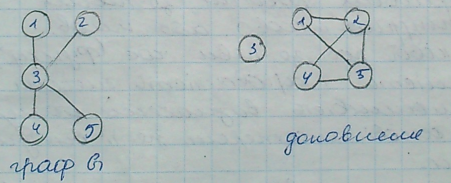
Може розглядатись у двох вар.: доповнення графа відносно іншого заданого графа; доповнення відносно універсального або повнозв’язного графа.
Універсальний граф – це граф у якого є ребра між кожною парою вершин.