- •Л.Е. Нестерова, и.В. Матвеев
- •Глава 1. Дифференциальные уравненимя первого порядка 6
- •Глава 2. Понижение порядка дифференциальных уравнений 48
- •Глава 3. Линейные дифференциальные уравнения высших порядков 55
- •Глава 4. Системы дифференциальных уравнений 82
- •Введение
- •Глава 1. Дифференциальные уравненимя первого порядка Основные понятия и определения
- •Уравнения с разделенными и разделяющимися переменными
- •Дифференциальные уравнения, однородные относительно х,уи приводящиеся к ним
- •Обобщенные однородные дифференциальные уравнения.
- •Линейные уравнения первого порядка и приводящие к ним
- •Уравнения в полных дифференциалах
- •Уравнения первого порядка n-степени, не разрешенные относительно производной
- •Задача Коши для дифференциального уравнения 1-го порядка.
- •Особые точки. Особые решения
- •Метод Пикара
- •Численные методы решения задачи Коши
- •Контрольные вопросы
- •Глава 2. Понижение порядка дифференциальных уравнений Уравнения высшего порядка. Общие сведения
- •Уравнения высших порядков, допускающие понижение порядка
- •Контрольные вопросы
- •Глава 3. Линейные дифференциальные уравнения высших порядков Основные понятия и определения
- •Линейные однородные дифференциальные уравнения. Свойства решений линейных однородных дифференциальных уравнений
- •Линейная зависимость функций. Определитель Вронского и его применения
- •Фундаментальная система решений линейного однородного дифференциального уравнения
- •Теорема о структуре общего решения линейного однородного дифференциального уравнения
- •Свойства решений линейного неоднородного дифференциального уравнения
- •Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных
- •Линейные однородные дифференциальные уравненияn-порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравненияn -го порядка с постоянными коэффициентами
- •Контрольные вопросы
- •Глава 4. Системы дифференциальных уравнений Основные понятия и определения
- •Интегрирование нормальных систем дифференциальных уравнений методом исключения неизвестных.
- •Линейные системы дифференциальных уравнений
- •Свойства решений линейных однородных систем дифференциальных уравнений
- •Фундаментальная система решений линейной однородной системы дифференциальных уравнений
- •Теорема о структуре общего решения линейной однородной системы дифференциальных уравнений
- •Линейные неоднородные системы дифференциальных уравнений
- •Интегрирование линейных неоднородных систем дифференциальных уравнений методом вариации постоянных
- •Линейные неоднородные системы дифференциальных уравнений с постоянными коэффициентами
- •Контрольные вопросы
- •Список литературы
Особые точки. Особые решения
Если
дифференциальное уравнение
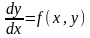 в некоторой области
в некоторой области
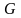 удовлетворяет всем условиям теоремы
Пикара, то через каждую точку этой
области проходит единственная интегральная
кривая и тогда эти точки области
называют обыкновенными.
удовлетворяет всем условиям теоремы
Пикара, то через каждую точку этой
области проходит единственная интегральная
кривая и тогда эти точки области
называют обыкновенными.
Наряду с этими, рассматривают точки, через которые не проходит не одной интегральной кривой или проходит не единственная интегральная кривая. Такие точки называются особыми.
Интегральная кривая, сплошь состоящая из особых точек, называется особой интегральной кривой. Решение, графиком которого является особая кривая, называется особым решением.
Особое решение следует искать, выделяя такие совокупности точек, в которых нарушаются условия теоремы Пикара.
Из двух условий, при которых существует единственное решение задачи Коши первое условие (непрерывность правой части) нарушается гораздо реже чем второе условие (условие Липшица).
Вместо второго условия можно рассматривать более грубое условие ограниченности производной правой части по y, т.е.
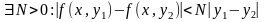
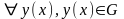 .
.
Точки,
в которых нарушается условие ограниченности
производной можно определить из уравнения
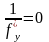 .
.
Заметим, что условия теоремы Пикара являются лишь достаточными, но не необходимыми, потому не все точки, в которых нарушаются эти условия, являются особыми точками.
Поведение интегральных кривых в окрестности особой точки может быть весьма разнообразным.
Некоторые
типы особых точек.1.
Уравнение
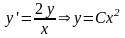 ,
интегральные кривые в этом случае
представляют собой семейство парабол
с вершиной в начале координат. Точка
(0,0) является особой точкой и называется
узлом.
,
интегральные кривые в этом случае
представляют собой семейство парабол
с вершиной в начале координат. Точка
(0,0) является особой точкой и называется
узлом.
2.
Уравнение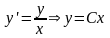 ,
интегральные кривые в этом случае
представляют собой семейство прямых,
проходящих через начало координат
(отличие от предыдущего случая в том,
что любая интегральная кривая в особой
точке имеет свое направление). Точка
(0,0) является особой точкой и называется
дикритическим
узлом.
,
интегральные кривые в этом случае
представляют собой семейство прямых,
проходящих через начало координат
(отличие от предыдущего случая в том,
что любая интегральная кривая в особой
точке имеет свое направление). Точка
(0,0) является особой точкой и называется
дикритическим
узлом.
3.
Уравнение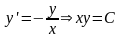 ,
интегральные кривые в этом случае
представляют собой семейство
гипербол, асимптотами которых служат
оси координат x=0,y=0.
Точка (0,0) является особой точкой и
называется седловиной.
,
интегральные кривые в этом случае
представляют собой семейство
гипербол, асимптотами которых служат
оси координат x=0,y=0.
Точка (0,0) является особой точкой и
называется седловиной.
4.
Уравнение 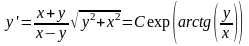 ,
интегральные кривые в этом случае
представляют собой семейство
логарифмических спиралей вокруг начала
координат. Точка (0,0) является особой
точкой и называется фокусом.
,
интегральные кривые в этом случае
представляют собой семейство
логарифмических спиралей вокруг начала
координат. Точка (0,0) является особой
точкой и называется фокусом.
5. Уравнение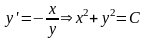 .
Через саму особую точку (0,0) не проходит
ни одной интегральной кривой. Точка
(0,0) является особой точкой и называется
центром. Интегральные кривые в этом
случае представляют собой концентрические
окружности.
.
Через саму особую точку (0,0) не проходит
ни одной интегральной кривой. Точка
(0,0) является особой точкой и называется
центром. Интегральные кривые в этом
случае представляют собой концентрические
окружности.
Метод Пикара
Процесс
нахождения решения по методу Пикара
основан на использовании интегрального
уравнения
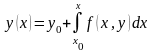 и
сводится к построению последовательного
приближения Пикара по формуле
и
сводится к построению последовательного
приближения Пикара по формуле
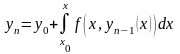 ,
n=1,2,…
,
n=1,2,…
Пример 1.
Пусть задано дифференциальное уравнение и начальные условия вида (задача Коши)
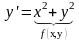 ,
,
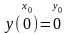 .
.
Тогда
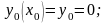
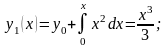
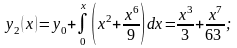
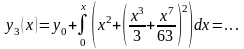
Метод Пикара имеет просто вычисляемую погрешность
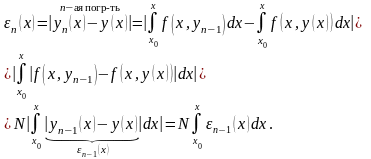 .
.
То есть погрешность на n-ом шаге вычисляется через погрешность на предыдущем шаге по формуле
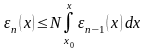 ,
n=1,2,…
,
n=1,2,…
Теперь вычислим погрешность для нулевого, первого, второго и n-ого приближения (на 0-м, 1-м и n-шаге):
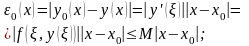
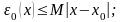
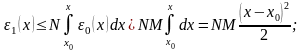
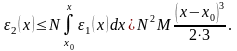
Тогда
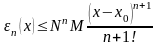 -формула
для вычисления погрешности.
-формула
для вычисления погрешности.
Пример 2. Найти решение задачи Коши
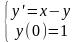 ,
,
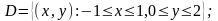
построить
4-е приближение
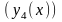 по методу Пикара и оценить погрешность.
по методу Пикара и оценить погрешность.
Решение.
Максимальное значение функции в области D
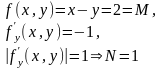
N– оценка постоянной Липшица,
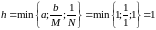 –
интервал
определения решения.
–
интервал
определения решения.
Погрешность на 4-м шаге
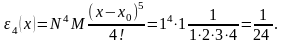
Четвёртое приближение по методу Пикара строится следующим образом:
1)
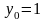 ;
;
2)
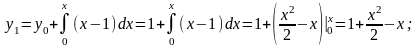
3)
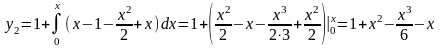 ;
;
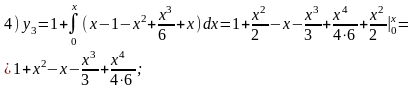
5)