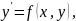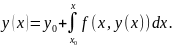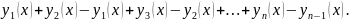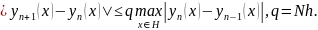- •Л.Е. Нестерова, и.В. Матвеев
- •Глава 1. Дифференциальные уравненимя первого порядка 6
- •Глава 2. Понижение порядка дифференциальных уравнений 48
- •Глава 3. Линейные дифференциальные уравнения высших порядков 55
- •Глава 4. Системы дифференциальных уравнений 82
- •Введение
- •Глава 1. Дифференциальные уравненимя первого порядка Основные понятия и определения
- •Уравнения с разделенными и разделяющимися переменными
- •Дифференциальные уравнения, однородные относительно х,уи приводящиеся к ним
- •Обобщенные однородные дифференциальные уравнения.
- •Линейные уравнения первого порядка и приводящие к ним
- •Уравнения в полных дифференциалах
- •Уравнения первого порядка n-степени, не разрешенные относительно производной
- •Задача Коши для дифференциального уравнения 1-го порядка.
- •Особые точки. Особые решения
- •Метод Пикара
- •Численные методы решения задачи Коши
- •Контрольные вопросы
- •Глава 2. Понижение порядка дифференциальных уравнений Уравнения высшего порядка. Общие сведения
- •Уравнения высших порядков, допускающие понижение порядка
- •Контрольные вопросы
- •Глава 3. Линейные дифференциальные уравнения высших порядков Основные понятия и определения
- •Линейные однородные дифференциальные уравнения. Свойства решений линейных однородных дифференциальных уравнений
- •Линейная зависимость функций. Определитель Вронского и его применения
- •Фундаментальная система решений линейного однородного дифференциального уравнения
- •Теорема о структуре общего решения линейного однородного дифференциального уравнения
- •Свойства решений линейного неоднородного дифференциального уравнения
- •Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных
- •Линейные однородные дифференциальные уравненияn-порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравненияn -го порядка с постоянными коэффициентами
- •Контрольные вопросы
- •Глава 4. Системы дифференциальных уравнений Основные понятия и определения
- •Интегрирование нормальных систем дифференциальных уравнений методом исключения неизвестных.
- •Линейные системы дифференциальных уравнений
- •Свойства решений линейных однородных систем дифференциальных уравнений
- •Фундаментальная система решений линейной однородной системы дифференциальных уравнений
- •Теорема о структуре общего решения линейной однородной системы дифференциальных уравнений
- •Линейные неоднородные системы дифференциальных уравнений
- •Интегрирование линейных неоднородных систем дифференциальных уравнений методом вариации постоянных
- •Линейные неоднородные системы дифференциальных уравнений с постоянными коэффициентами
- •Контрольные вопросы
- •Список литературы
Задача Коши для дифференциального уравнения 1-го порядка.
Теорема о существовании единственного решения задачи Коши
Функция
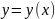 удовлетворяет условию
Липшица на
удовлетворяет условию
Липшица на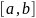 ,если
,если
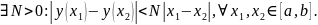
Лемма 1. Если функция удовлетворяет условию Липшшица на , то она будет непрерывной на этом отрезке.
Лемма 2. Если функция дифференцируема на ,то есть
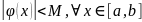 ,
то эта функция удовлетворяет условию
Липшица.
,
то эта функция удовлетворяет условию
Липшица.
Рассмотрим задачу Коши
|
(1.54) |
|
(1.55) |
- задачу нахождения решения(1.54), удовлетворяющее условию (1.55).
Для задачи Коши существует ряд теорем о существовании и единственности ее решения.
Из всех теорем наиболее удачной является теорема Пикара, так как эта теорема наряду с доказательством позволяет построить приближённый метод нахождения решения задачи Коши.
Теорема
Пикара.
Пусть
функция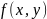 ,
то есть правая часть дифференциального
уравнения (1.54) определена и непрерывна
в области
,
то есть правая часть дифференциального
уравнения (1.54) определена и непрерывна
в области
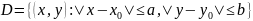 и
в каждой точке этой области удовлетворяет
условию Липшица по
, то есть
и
в каждой точке этой области удовлетворяет
условию Липшица по
, то есть
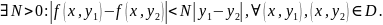
Тогда существует единственное решение дифференциального уравнения (1.54), удовлетворяющее начальному условию (1.55), определённое в интервале
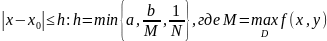
Доказательство.
Дана задача Коши
|
(1.56) |
|
(1.57) |
Пусть является решением задачи Коши (1),(2).
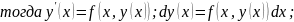 интегрируя,
получим
интегрируя,
получим
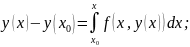 тогда
тогда
|
(1.58) |
Уравнение (1.58), в котором искомая функция входит под знак интеграла, называется интегральным уравнением.
Интегральное уравнение (1.58) эквивалентно задачи Коши (1.56), (1.57).
Построим
последовательность функций
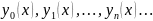 ,здесь
,здесь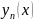 –
–
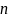 -ое
последовательное приближения Пикара(примем
в качестве
-ое
последовательное приближения Пикара(примем
в качестве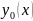 начальное
условие). То есть:
начальное
условие). То есть:
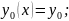
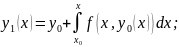
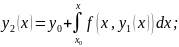
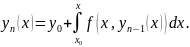
Пусть
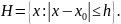
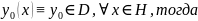
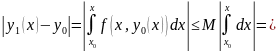
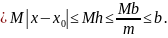
Следовательно,
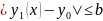 .
.
Значит
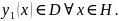
Пусть
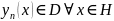
Тогда
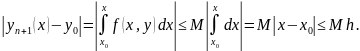
Следовательно,
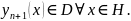
Таким
образом, доказано, что построенная
последовательность функций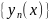 ,являющаяся
последовательным приближением Пикара,
существует.
,являющаяся
последовательным приближением Пикара,
существует.
Докажем, что последовательность функции сходится к некоторой непрерывной функции, то есть
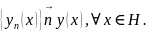
Для
этого представим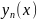 следующим
образом
следующим
образом
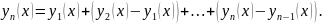
Для того, чтобы доказать сходимость последовательности, достаточно доказать, что сходится ряд
|
(1.59) |
Рассмотрим
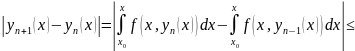
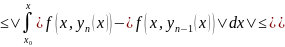
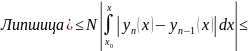
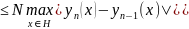 hили
hили
|
|
Выберем С так, чтобы выполнялись условия
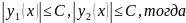
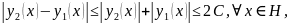
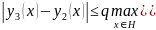
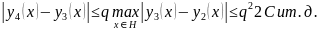
Таким образом, доказано, что члены ряда (1.59) по абсолютной величине не превышают соответствующих членов ряда
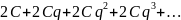 ,
,
который
будет сходиться при условии, что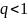 то есть
то есть
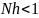 .
.
Но
тогда в соответствии признаком
Вейерштрасса функциональный ряд(1.59)
сходится равномерно на Н, и пределом
или суммой этого ряда является функция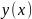 ,
непрерывная на
,
непрерывная на
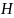 ,
то есть
,
то есть
Докажем,
что эта функция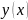 является
решением интегрального уравнения (3),
то есть
является
решением интегрального уравнения (3),
то есть
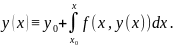
Рассмотрим n-ое приближения Пикара
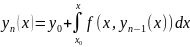
и
перейдём к пределу при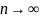
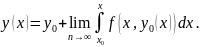
Чтобы
доказать, что
–решение уравнения (1.58),необходимо
показать, что
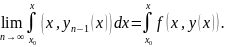
Для этого рассмотрим разность интегралов
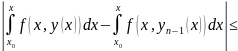
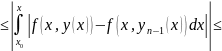
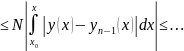
Далее в силу равномерной сходимости последовательности
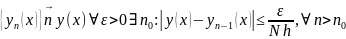 ,
имеем
,
имеем
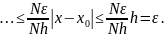
Таким
образом, мы доказали, что каково ни было
выбрано
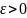 ,
можно указать номер
,
можно указать номер
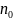 начиная с которого выполняется
неравенство:
начиная с которого выполняется
неравенство:
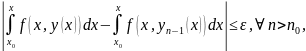
а это и означает, что
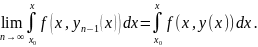
Таким образом, доказано, что функция , являющаяся пределом последовательности ,есть не что иное, как решение интегрального уравнения(1.58), а значит и решение задачи Коши(1.56), (1.57).Тем самым мы доказали, что решение существует.
Докажем единственность решения. Рассуждаем от противного.
Предположим
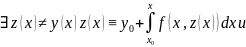
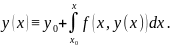
Вычтем эти уравнения почленно и вычислим модуль разности
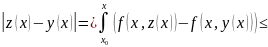
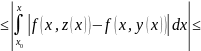
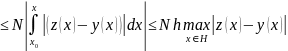 .
.
Таким
образом, мы получили оценочную формулу
из которой следует, что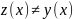 при
при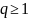 ,
но это противоречит полученному ранее
условию.
,
но это противоречит полученному ранее
условию.
Полученное противоречие доказывает, что другого решения, отличного от не существует.