Интегрирование нормальных систем дифференциальных уравнений методом исключения неизвестных.

Этот метод называется иногда методом сведения системы дифференциальных уравнений к дифференциальному уравнению высшего порядка.

Этот метод является наиболее универсальным методом интегрирования нормальных систем дифференциальных уравнений.

Из уравнений системы путём дифференцирования исключают все неизвестные функции кроме одной, относительно которой получают одно дифференциальное уравнение n-го порядка.

Полученное уравнение интегрируют известными способами. В результате находим одну неизвестную функцию. Остальные неизвестные функции находят по возможности без интегрирования из формул, полученных при исключении неизвестных функций.

Пример. Найти решение нормальной системы дифференциальных уравнений.

Решение.

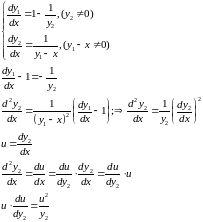
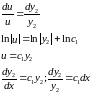
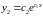- найдена первая неизвестная функция.

Подставляем найденную функцию во второе уравнение системы и получаем:

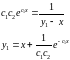
Найдена вторая неизвестная функция, тем самым найдено решение заданной нормальной системы дифференциальных уравнения.

Линейные системы дифференциальных уравнений

Линейной системой дифференциальных уравнений называют систему таких уравнений, в которой неизвестные функции и их производные входят линейно.

Таким образом, нормальная линейная система запишется в виде

(4.5)

Введем обозначение

, ,

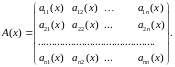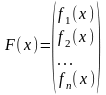тогда систему (4.5) можно записать в матричной форме

(4.6)

Для того чтобы система (4.5)с заданными начальными условиями имела единственное решение, достаточно, чтобы функции a_ij(x), i, j = 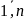были непрерывными на рассматриваемом отрезке [a,b].

Свойства решений линейных однородных систем дифференциальных уравнений

Линейная система (4.6) в случае, если 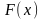тождественно равна 0, называется линейной однородной системой дифференциальных уравнений(ЛОСДУ).

(4.7)

где a_ij(x) - непрерывные на [a,b] функции.

Такие системы обладают свойствами, которые могут быть сформулированы в виде следующих теорем:

Теорема 1. Если вектор-функции 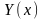является решением линейной однородной системы дифференциальных уравнений (4.7), то вектор-функция 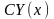, гдеС- произвольная постоянная, также является решением этой системы.

Доказательство.

Пусть - решение системы (4.7), тогда _.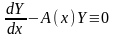

Покажем, что также является решением системы (4.7).

Подставим в систему (4.7) вектор-функцию , получим:

_.

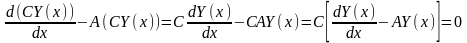Следовательно, если - решение системы (4.7), то и - также решение системы (4.7).

Теорема 2.Сумма двух решений линейной однородной системы дифференциальных уравнений есть также решение этой системы.

Доказательство.

Пусть 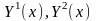вектор-функции, являющиеся решением системы (4.7).

Доказательство аналогично доказательству второго свойства решений ЛОДУ n-го порядка, рассмотренного в главе 3.

Теорема 3. Линейная комбинация с произвольными постоянными коэффициентами решений 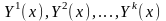ЛОСДУ является решением этой системы.

Доказательство.

Пусть есть решения системы (4.7). Покажем, что функция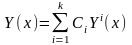 является решением системы (4.7).

Дальнейшее доказательство аналогично доказательству третьего свойства решений ЛОДУ n-го порядка, рассмотренного в главе 3.

Теорема 4.Пусть линейная однородная система дифференциальных уравнений (4.7) имеет комплексное решение: 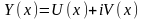, тогда действительная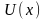 и мнимая 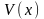части этого комплексного решения в отдельности также являются решениями этой системы. Здесь и - действительные вектор-функции

Доказательство.

Доказательство аналогично доказательству четвертого свойства решений ЛОДУ n-го порядка, рассмотренного в главе 3.