3. Криптоалгоритмы замены

Простые шифры включают в себя шифры перестановки, шифры замены и шифры гаммирования.

Шифр перестановки – это шифр, при помощи которого изменяется только порядок следования символов исходного текста, не изменяя их самих.

Шифр замены – это шифр, который осуществляется путем замены каждого символа открытого сообщения на другие символы.

Шифр гаммирования заключается в генерации гаммы шифра с помощью датчика псевдослучайных чисел и наложении полученной гаммы на открытые данные обратимым образом (например используя сложение по модулю 2).

Рассмотрим подробнее шифры замены.

Шифрами замены называют такие шифры, которые осуществляются путем замены каждого символа открытого сообщения на другие символы – шифрообозначения. Формально шифр замены можно описать следующим образом. Для каждой буквы а исходного алфавита строится некоторое множество символов M_a, которое называется множеством шифрообозначений для буквы а. Таблица является ключом шифра замены. Зная её, можно осуществить как зашифрование, так и расшифрование. При зашифрование каждая буква а открытого сообщения, начиная с первой, заменяется любым символом из множества M_a . За счет этого можно получить различные варианты зашифрованного сообщения для одного и того же открытого сообщения.

Таблица 1 – Шифры простой замены

А	Б	…	Я
Ма	Мб	…	Мя

В этом простейшем случае множество шифрообозначений M_a состоит из одного элемента.

Подстановка Цезаря.

Шифр Цезаря - один из самых простых и наиболее широко известных методов шифрования. Шифр Цезаря - это вид шифра подстановки, в котором каждый символ в открытом тексте заменяется буквой находящейся на некоторое постоянное число позиций правее него в алфавите.

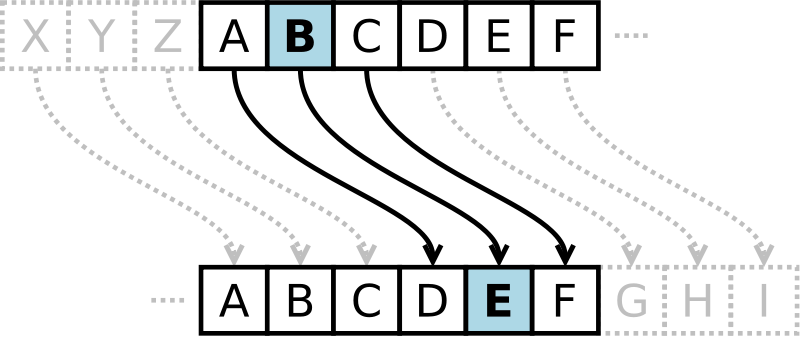
Рисунок 2 – Шифр Цезаря

Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки со своими генералами.

Математическая модель:

Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:

где x– символ открытого текста, y– символ шифрованного текста, n— мощность алфавита, а k— ключ.

Пример:

Шифрование с использованием ключа k = 3. Буква «С» «сдвигается» на три буквы вперед и становится буквой «Ф». Твердый знак, перемещённый на три буквы вперед, становится буквой «Э», и так далее:

Исходный алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

Шифрованный: ГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВ

Оригинальный текст:

Съешь же ещё этих мягких французских булок, да выпей чаю.

Шифрованный текст получается путём замены каждой буквы оригинального текста соответствующей буквой шифрованного алфавита:

Фэзыя йз зьи ахлш пвёнлш чугрщцкфнлш дцосн, жг еютзм ъгб .

Аффинная подстановка Цезаря

Аффинный шифр — это частный случай более общего многоалфавитного шифра подстановки. В аффинном шифре каждой букве алфавита размера m ставится в соответствие число из диапазона 0..m − 1. Затем при помощи модульной арифметики для каждого числа, соответствующего букве исходного алфавита, вычисляется новое число, которое заменит старое в шифротексте. Функция шифрования для каждой буквы

где модуль m — размер алфавита, а пара a и b — ключ шифра. Значение a должно быть выбрано таким, что a и m — взаимно простые числа.

Функция расшифрования:

где – обратное к a число по модулю m. То есть оно удовлетворяет уравнению:

Обратное к a число существует только в том случае, когда a и m — взаимно простые. Значит, при отсутствии ограничений на выбор числа a расшифрование может оказаться невозможным.

Пример:

В следующих примерах используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице. Таблица 2 – Алфавит

А	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25

Зашифрование

В этом примере необходимо зашифровать сообщение "ATTACK AT DAWN", используя упомянутое выше соответствие между буквами и числами, и значения a = 3, b = 4 и m = 26, так как в используемом алфавите 26 букв. Только на число a наложены ограничения, так как оно должно быть взаимно простым с 26. Возможные значения a: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 и 25. Значение b может быть любым, только если a не равно единице, так как это сдвиг шифра. Итак, для нашего примера функция шифрования:

y = E(x) = (3x + 4) mod 26.

Первый шаг зашифрования — запись чисел, соответствующих каждой букве сообщения. Затем, для каждого значения x найдем значение (3x + 4) и для каждого символа возьмем остаток от деления (3x + 4) на 26. Последний шаг процесса шифрования заключается в подстановке вместо каждого числа соответствующей ему буквы. В этом примере шифротекст будет "EJJEKIEJNESR". Таблица ниже показывает все шаги по зашифрованию сообщения аффинным шифром.

Таблица 3 – Шаги по зашифрованию сообщения аффинным шифром

Сообщение	A	T	T	А	C	K	A	T	D	A	W	N
x	0	19	19	0	2	10	0	19	3	0	22	13
3x + 4	4	61	61	4	10	34	4	61	13	4	70	43
(3x + 4)mod 26	4	9	9	4	10	8	4	9	13	4	18	17
Шифротекст	E	J	J	E	K	I	E	J	N	E	S	R

Расшифрование

Для расшифрования возьмем шифротекст из примера с шифрованием. Функция расшифрования будет D(y) = a ^{− 1}(y − b) mod 26, где a ^{− 1} = 9, b = 4 и m = 26. Для начала запишем численные значения для каждой буквы шифротекста. Затем рассчитаем для каждого символа 9(y − 4) и возьмем остаток от деления этого числа на 26.. Последний шаг операции расшифрования для шифротескста — поставить в соответствие числам буквы. Сообщение после расшифрования будет "ATTACKATDAWN". Таблица ниже показывает выполнение шагов.

Таблица 4 – Шаги по расшифрованию сообщения аффинным шифром

шифротекст	E	J	J	E	K	I	E	J	N	E	S	R
y	4	9	9	4	10	8	4	9	13	4	18	17
9(y − 4)	0	45	45	0	54	36	0	45	81	0	126	117
9(y − 4) mod 26	0	19	19	0	2	10	0	19	3	0	22	13
сообщение	A	T	T	А	C	K	A	T	D	A	W	N