Расчёт валов. Факторы, влияющие на критические скорости

Расчёт вала сводится к решению задач:

1. Известны скорости вращения, определить диаметр;

2. Известные геометрические параметры, определить скорости при которых деформации максимальные.

Из практики замечено, что при увеличении угловой скорости вал увеличивает прогиб. Затем при каком-то значении скорости количественные значения и деформация начинает уменьшаться. Вал занимает положение устойчивого равновесия.

Эта мгновение и резкие изменения деформаций соответствуют максимальным скоростям. Скорости называются критическими.

Определение критичных скоростей

При определении критичных скоростей в принципе используют метод Данкерли и метод Рейлея.

Метод Рейлея (энергетический метод) заключается в том, что используется закон сохранения энергии.

Предполагается, что в любой момент времени сумма кинетической и потенциальной энергии, накапливаемая системой за счёт динамических деформаций, есть величина постоянная, используется метод наложения.

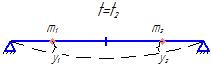
На однопролётный вал закрепляются 2-е массы и . Предполагается, что в какой-то момент времени под действием динамических нагрузок вал прогибается и получает деформации и .

В этом методе задается величина предполагаемых деформаций «у». В основу метода положено условие, что известно соотношение между деформациями и колеблющимися массами.

В какой-то момент времени система находится в положении динамического равновесия. Считается, что в этот момент потенциальная энергия U=0. .

Т.к. сумма кинетической и потенциальной энергии величина постоянная, то максимальному значению ( .

В какой-то момент времени деформации переходят по другую сторону относительно центральной оси вала и в какой-то момент занимают положение равновесия, т.е. все точки системы меняют знак подобно самоцентрированию.

В этом случае в данный момент их скорости равны нулю и T=0,

; ; ;

При расчётах предполагается, что деформации и потенциальная энергия вырывается через работу внешних сил. За внешние силы принимается момент инерции системы.

После преобразований: ;

Метод Данкерли:

;

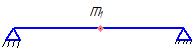
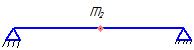
После преобразований: ;

На основании приближенных методов Данкерли и Рейлея за основу расчёта критических скоростей берётся скорость: и ;

; ;

Факторы, влияющие на критические скорости

В реальных условиях масса вала, соизмерима с массой насаженных на вал деталей.

Неучёт массы вала приводит к большим погрешностям. Учесть массу валов при реальных условиях трудно, поэтому при расчётах пользоваться приближенным методам Крылова.

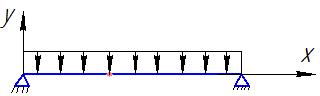
Предполагается вал – это балка с равномерно-распределённой нагрузкой. Уравнение деформации вращающегося вала имеет вид:

– меняющая действующая динамическая нагрузка.

За динамическую нагрузку принимается центробежная сила

; - масса единицы длины вала. При решении задачи получается: , где - корень частного уравнения; ;

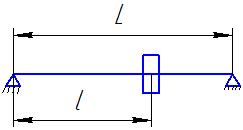
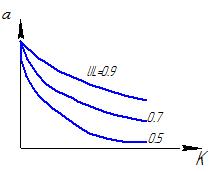
, (172) « » находится в зависимости от коэффициента «К» .