1.
Абсцисса
градиента функции
в точке
равна:
A) 2
10.
Дивергенция
вектора
равна:
A)
14.
Какой
вариант типов полей из нижеперечисленных
подходят к векторному полю
?
A) не потенциальное, не соленоидальное, не гармоническое
15.
Какой
вариант типов полей из нижеперечисленных
подходят к векторному полю
?
A) потенциальное, не соленоидальное, не гармоническое
16.
Какой
вариант типов полей из нижеперечисленных
подходят к векторному полю
?
A) потенциальное, не соленоидальное, не гармоническое
17.
Какой
вариант типов полей из нижеперечисленных
подходят к векторному полю
?
A) не потенциальное, не соленоидальное, не гармоническое
18.
Какой
вариант типов полей из нижеперечисленных
подходят к векторному полю
?
A) потенциальное, не соленоидальное, не гармоническое
19.
Система
дифференциальных уравнений для
определения векторных линий векторного
поля
имеет вид:
A)
3.
Формула
для вычисления потока векторного поля
через поверхность
:
A)
4.
Формула
для вычисления потока векторного поля
через поверхность
:
A)
7.
Пользуясь
формулой Гаусса-Остроградского поток
векторного поля
через замкнутую поверхность
,
окружающую область
,
в виде тройного интеграла имеет вид:
A)
11.
Формула
циркуляции вектора
вдоль линии
имеет вид:
A)
14. Ротор векторного поля равен:
A)
17.
Абсцисса
ротора векторного
поля
равна:
A)
18.
Ордината
ротора векторного
поля
равна:
A)
19.
Абсцисса
ротора векторного
поля
равна:
A)
20.
Аппликата
ротора векторного
поля
равна:
A)
1.
Уравнение
линии уровня скалярного
поля
,
проходящей через точку
имеет вид:
A)
2.
Уравнение
линии уровня скалярного
поля
,
проходящей через точку
имеет вид:
A)
3.
Уравнение
линии уровня скалярного
поля
,
проходящей через точку
имеет вид:
A)
4.
Уравнение
линии уровня скалярного
поля
,
проходящей через точку
имеет вид:
A)
5.
Уравнение
линии уровня скалярного
поля
,
проходящей через точку
имеет вид:
A)
6.
Наибольшая
скорость возрастания функции
в точке
равна:
A)
7.
Наибольшая
скорость возрастания функции
в точке
равна:
A)
8.
Наибольшая
скорость возрастания функции
в точке
равна:
A)
9.
Наибольшая
скорость возрастания функции
в точке
равна:
A)
10.
Наибольшая
скорость возрастания функции
в точке
равна:
A)
11.
Производная
функции
в точке
в направлении вектора
равна:
A)
12.
Производная
функции
в точке
в направлении вектора
равна:
A)
13.
Производная
функции
в точке
в направлении вектора
равна:
A)
14.
Производная
функции
в точке
в направлении вектора
равна:
A)
15.
Производная
функции
в точке
в направлении вектора
равна:
A)
16.
Производная
функции
в точке
в направлении вектора
равна:
A)
17.
Производная
функции
в точке
в направлении вектора
равна:
A)
18.
Производная
функции
в точке
в направлении вектора
равна:
A)
19.
Производная
функции
в точке
в направлении вектора
равна:
A)
20.
Градиент
функции
в точке
равен:
A)
1.
Градиент
функции
в точке
равен:
A)
2.
Градиент
функции
в точке
равен:
A)
3.
Градиент
функции
в точке
равен:
A)
4.
Градиент
функции
в точке
равен:
A)
5.
Градиент
функции
в точке
равен:
A)
6.
Градиент
функции
в точке
равен:
A)
7.
Дивергенция
векторного поля
равна:
A)
8.
Дивергенция
векторного поля
равна:
A)
9.
Дивергенция
векторного поля
равна:
A)
10.
Дивергенция
векторного поля
равна:
A)
11.
Дивергенция
векторного поля
равна:
A)
12. Пользуясь формулой Гаусса-Остроградского поток векторного поля через замкнутую поверхность , окружающую область , в виде тройного интеграла имеет вид:
A)
13. Пользуясь формулой Гаусса-Остроградского поток векторного поля через замкнутую поверхность , окружающую область , в виде тройного интеграла имеет вид:
A)
14.
Пользуясь
формулой Гаусса-Остроградского поток
векторного поля
через замкнутую поверхность
,
окружающую область
,
в виде тройного интеграла имеет вид:
A)
15. Пользуясь формулой Гаусса-Остроградского поток векторного поля через замкнутую поверхность , окружающую область , в виде тройного интеграла имеет вид:
A)
16.
Пользуясь
формулой Гаусса-Остроградского поток
векторного поля
через замкнутую поверхность
,
окружающую область
,
в виде тройного интеграла имеет вид:
A)
17.
Формула
для вычисления потока векторного поля
через поверхность
имеет вид:
A)
18.
Формула
для вычисления потока векторного поля
через поверхность
имеет вид:
A)
19.
Формула
для вычисления потока векторного поля
через поверхность
имеет вид:
A)
20.
Формула
для вычисления потока векторного поля
через поверхность
имеет вид:
A)
1.
,
тогда производная функции
по направлению вектора
равна:
A)
2.
,
тогда производная функции
по направлению вектора
равна:
A)
3.
,
тогда производная функции
по направлению вектора
равна:
A)
4.
,
тогда производная функции
по направлению вектора
равна:
A)
5.
,
тогда производная функции
по направлению вектора
равна:
A)
6.
Ротор
векторного
поля
равен:
A)
7.
Ротор
векторного
поля
равен:
A)
8.
Ротор
векторного
поля
равен:
A)
9.
Ротор
векторного
поля
равен:
A)
10.
Ротор
векторного
поля
равен:
A)
11.
Циркуляция
вектора
вдоль линии
имеет вид:
A)
12.
Циркуляция
вектора
вдоль линии
имеет вид:
A)
13.
Циркуляция
вектора
вдоль линии
имеет вид:
A)
14.
Циркуляция
вектора
вдоль линии
имеет вид:
A)
15.
Циркуляция
вектора
вдоль линии
имеет вид:
A)
16.
Система
дифференциальных уравнений для
определения векторных линий векторного
поля
имеет вид:
A)
17.
Система
дифференциальных уравнений для
определения векторных линий векторного
поля
имеет вид:
A)
18.
Система
дифференциальных уравнений для
определения векторных линий векторного
поля
имеет вид:
A)
19.
Система
дифференциальных уравнений для
определения векторных линий векторного
поля
имеет вид:
A)
20.
Система
дифференциальных уравнений для
определения векторных линий векторного
поля
имеет вид:
A)
«Дифференциальные уравнения » Модуль2
1.
Порядок
дифференциального уравнения
равен.
A) 5
2.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
3. Общий интеграл или общее решение дифференциального уравнения имеет вид:
A)
4.
Если
функция
однородная, то её степень однородности
равна:
A) 0
5.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
6. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть:
A)
7.
Порядок
дифференциального уравнения
равен:
A) 4
8.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
9.
Общий
интеграл или общее решение дифференциального
уравнения
есть функция:
A)
10.
Если
функция
однородная, то её степень однородности
равна:
A) 0
11.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
12. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть функция:
A)
13.
Порядок
дифференциального уравнения
равен:
A) 3
14.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
15.
Общий
интеграл или общее решение дифференциального
уравнения
есть функция:
A)
16.
Если
функция
однородная, то её степень однородности
равна:
A) 1
17.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
18. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть функция:
A)
19.
Порядок
дифференциального уравнения
равен:
A) 3
20.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
1.
Общий
интеграл или общее решение дифференциального
уравнения
есть функция:
A)
2.
Если
функция
однородная, то её степень однородности
равна:
A) 2
3.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
4. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть функция:
A)
5.
Порядок
дифференциального уравнения
равен.
A) 4
6.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
7. Общий интеграл или общее решение дифференциального уравнения имеет вид:
A)
8.
Если
функция
однородная, то её степень однородности
равна:
A) 0
9.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
10. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть функция:
A)
11.
Порядок
дифференциального уравнения
равен:
A) 3
12.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
13.
Общий
интеграл или общее решение дифференциального
уравнения
имеет вид:
A)
14.
Если
функция
однородная,то её степень однородности
равна:
A) 1
15.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
16. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть функция:
A)
17.
Дифференциальное
уравнение
является дифференциальным уравнением
типа:
A) с разделяющимися переменными
18.
Общее
решение дифференциального уравнения
содержит постоянных:
A) 3
19.
Структура
частного решения неоднородного линейного
дифференциального уравнения
,
если характеристическое уравнение
соответствующего однородного линейного
дифференциального уравнения
имеет корни:
,
определяется видом:
A)
20. Общее решение дифференциального уравнения содержит постоянных:
A) 3
1.
Дифференциальное
уравнение
является дифференциальным уравнением
типа:
A) однородным
2.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
3.
Чтобы
понизить порядок дифференциального
уравнения
необходимо применить замену:
A)
4.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
5. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами есть:
A)
6.
Структура
частного решения неоднородного линейного
дифференциального уравнения
,
если характеристическое уравнение
соответствующего однородного линейного
дифференциального уравнения имеет
корни:
,
определяется видом:
A)
7.
Структура
частного решения неоднородного линейного
дифференциального уравнения
,
если характеристическое уравнение
соответствующего однородного линейного
дифференциального уравнения имеет
корни:
,
определяется видом:
A)
8.
Общим
решением однородного линейного
дифференциального уравнения с постоянными
коэффициентами
является:
A)
9.
Характеристическое
уравнение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
10.
Дифференциальное
уравнение
является дифференциальным уравнением
типа:
A) однородным
11.
Дифференциальное
уравнение
приводится к уравнению с разделенными
переменными вида:
A)
12.
Общий
интеграл или общее решение уравнения
:
A)
13.
Чтобы
понизить порядок дифференциального
уравнения
,
необходимо использовать замену:
A)
14.
Характеристическое
уравнение дифференциального уравнения
имеет вид:
A)
15.
Общее
решение однородного линейного
дифференциального уравнения с постоянными
коэффициентами
есть функция:
A)
16.
Структура
частного решения неоднородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
17.
Структура
частного решения неоднородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
18.
Общее
решение дифференциального уравнения
содержит произвольных постоянных:
A) 5
19.
Уравнение
является дифференциальным уравнением:
A) линейным
20.
Уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными вида:
A)
1.
Общим
решением дифференциального уравнения
является:
A)
2.
Чтобы
понизить порядок дифференциального
уравнения
,
необходимо использовать замену:
A)
3.
Общее
решение дифференциального уравнения
содержит произвольных постоянных:
A) 4
4.
Характеристическое
уравнение дифференциального уравнения
имеет вид:
A)
5.
Однородное
линейное дифференциальное уравнение
имеет общее решение:
A)
6.
Структура
частного решения неоднородного линейного
дифференциального уравнения
имеет вид:
A)
7.
Структура
частного решения неоднородного линейного
дифференциального уравнения
имеет вид:
A)
8.
Уравнение
является дифференциальным уравнением:
A) в полных дифференциалах
9.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными:
A)
10.
Общим
решением линейного однородного уравнения
является:
A)
11.
Чтобы
понизить порядок дифференциального
уравнения
,
необходимо:
A) трижды интегрировать
12.
Общее
решение дифференциального уравнения
содержит произвольных постоянных:
A) 4
13.
Характеристическим
уравнением линейного однородного
уравнения с постоянными коэффициентами
является:
A)
14.
Общее
решение линейного однородного уравнения
с постоянными коэффициентами
есть функция:
A)
15.
Структура
частного решения неоднородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
16.
Структура
частного решения неоднородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
17.
Дифференциальное
уравнение первого порядка
является:
A) уравнением Бернулли
18.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделяющимися переменными:
A)
19.
Общим
решением линейного однородного уравнения
является:
A)
20.
Характеристическое
уравнение однородного линейного
дифференциального уравнения
с постоянными коэффициентами имеет
вид:
A)
1. Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами имеет вид:
A)
2.
Уравнение
является дифференциальным уравнением:
A) однородным
3.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделенными переменными:
A)
4.
Общее
решение линейного однородного уравнения
есть:
A)
5.
Характеристическое
уравнение однородного линейного
дифференциального уравнения
с постоянными коэффициентами имеет
вид:
A)
6.
Общим
решением однородного линейного
дифференциального уравнения
является:
A)
7.
Структура
частного решения неоднородного линейного
дифференциального уравнения с постоянными
коэффициентами
имеет вид:
A)
8.
Дифференциальное
уравнение
приводится к дифференциальному уравнению
с разделенными переменными:
A)
9.
Общим
решением линейного однородного уравнения
является:
A)
10.
Решением
задачи Коши дифференциального уравнения
с начальными условиями
и общим решением
является:
A)
11.
Решением
задачи Коши дифференциального уравнения
с начальными условиями
и общим решением
является:
A)
12.
Дифференциальное
уравнение первого порядка
является:
A) линейным
13. Дифференциальное уравнение приводится к дифференциальному уравнению с разделенными переменными вида:
A)
14.
Общим
решением однородного линейного
дифференциального уравнения с постоянными
коэффициентами
является:
A)
15.
Структура
частного решения неоднородного линейного
дифференциального уравнения
,
имеющего корни характеристического
уравнения
соответствующего однородного линейного
дифференциального уравнения, имеет
вид:
A)
16.
Если
корни характеристического уравнения
однородного линейного дифференциального
уравнения, соответствующего неоднородному
,
равны
,
то структура частного решения имеет
вид:
A)
17.
Чтобы
понизить порядок дифференциального
уравнения
,
необходимо:
A) интегрировать три раза
18.
Общим
решением линейного однородного уравнения
является:
A)
19.
Чтобы
понизить порядок дифференциального
уравнения
,
необходимо применить замену:
A)
«Ряды» (часть 1)
20.
Общий
член ряда
равен
A)
1.
Общий
член ряда
равен
A)
2.
Общий
член ряда
равен
A)
3.
Общий
член ряда
равен
A)
4.
Общий
член ряда
равен
A)
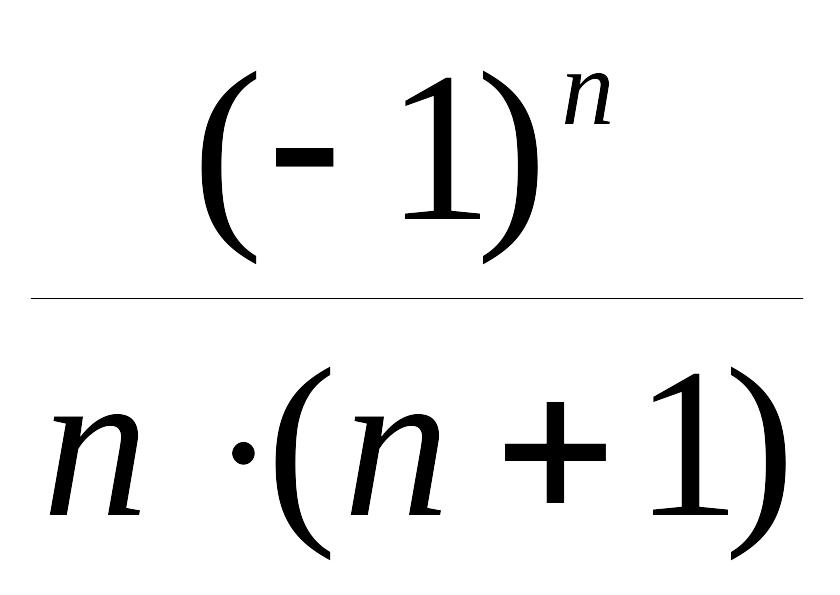
5.
Общий
член ряда
равен
A)
B
6.
Для
ряда
вычислите
A) 1/4
7.
Для
ряда
найдите
A) 1/2
8.
Для
ряда
найдите
A) 2
9.
Для
ряда
найдите
A) -1/6
10.
Для
ряда
найдите
A) -5/28
11.
Для
ряда
найдите
A) 1/3
12.
Для
ряда
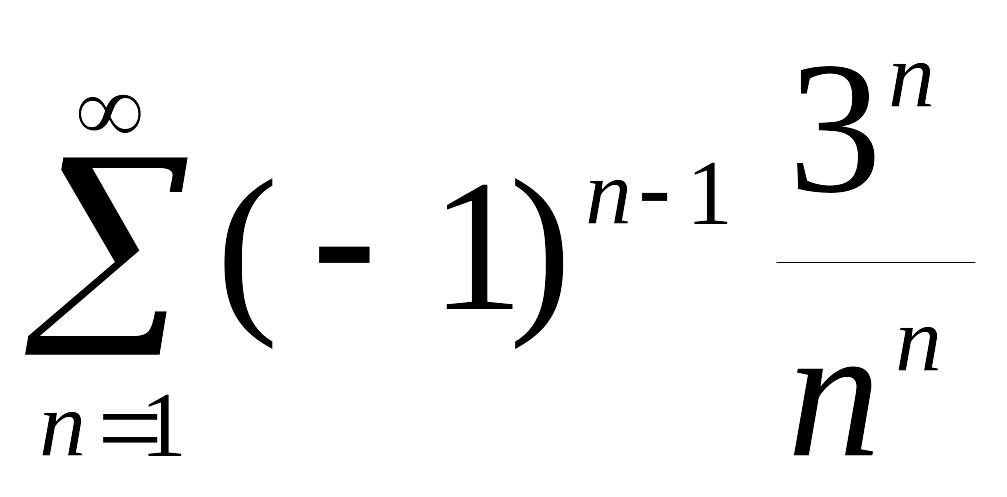найдите
A) 1
13.
Для
ряда
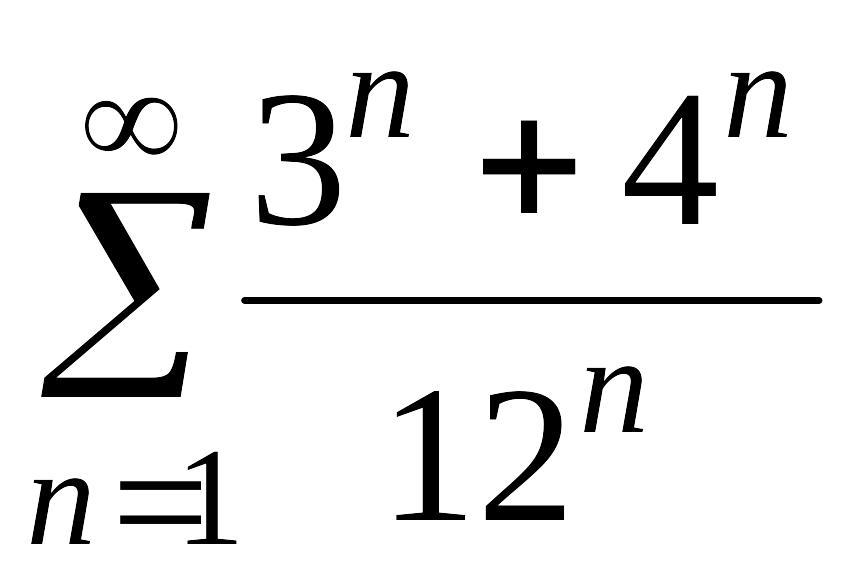найдите
A) 25/144
14.
Для
ряда
найдите
A) 31/12
15.
Для
ряда
найдите
A) 5/26
16.
Для
ряда
найдите
A) 16/39
17.
Ряд
называется сходящимся, если:
A)
cуществует
18.
Геометрическая
прогрессия
сходится
в случае
A) |q|<1
19.
Если
,
то ряд
A) может сходиться, а может и расходиться
20.
Если
частичная
сумма ряда
,
а S-его
сумма, то остаток этого ряда
равен
A)
1.
Если
ряд
сходится, а
,
то ряд
A) сходится
2.
Для
ряда
найти
A) 2/9
3. Согласно необходимому признаку, если ряд сходится, то
A)
cуществует
4.
Ряд
Дирихле,
сходится, если
A) р>1
5.
Согласно
признаку
Даламбера, если у ряда
имеется предел
то
A) ряд сходится , если q<1
6.
Исследуйте
ряд на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда
с рядом Дирихле
A) расходится р=1
7.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) расходится р=1
8.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) сходится р=2
9.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) расходится р=1
10.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) сходится р=2
11.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) сходится р=4
12.
Исследуйте
ряд на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда
с рядом Дирихле
A) сходится р=2
13.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) сходится р=3
14.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) сходится р=8
15.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
A) расходится р=1/3
16.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле.
A) расходится р=1/2
17.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак сравнения
18.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Необходимый признак сходимости
19.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак сравнения
20.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак сравнения
1.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Необходимый признак сходимости
2.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Необходимый признак сходимости
3.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Необходимый признак сходимости.
4.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
5.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Радикальный признак Коши
6.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Радикальный признак Коши
7.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
8.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак сравнения
9. Какой признак из перечисленных ниже, надо применить для исследования сходимости ряда
A) Признак сравнения
10.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
11.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
12.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
13.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
14.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
15.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
16.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
17.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Даламбера
18.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Радикальный признак Коши
19.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Радикальный признак Коши
20.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
1.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Интегральный признак
2.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Интегральный признак
3.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Интегральный признак
4.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
5.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
6.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
7. Какой признак из перечисленных ниже, надо применить для исследования сходимости ряда
A) Признак Лейбница
8.
Какой
признак из перечисленных ниже, надо
применить для исследования сходимости
ряда
A) Признак Лейбница
9. Cреди рядов (1) (2) (3) укажите сходящиеся условно
(1)
(2)
(3)
A) (2), (3)
10. Cреди рядов (1) (2) (3) укажите сходящиеся условно
(1)
(2)
(3)
A) (3), (2)
11. Cреди рядов (1) (2) (3) укажите расходящиеся ряды
(1)
,
(2)
,
(3)
A) (3), (1)
12. Cреди рядов (1) (2) (3) укажите сходящиеся условно
(1)
(2)
(3)
A) (2)
13. Cреди рядов (1), (2), (3) укажите сходящиеся условно
(1)
(2)
(3)
A) (3)
14. Cреди рядов (1) (2) (3) укажите сходящиеся ряды
(1)
,
(2)
,
(3)
A) (1)
15. Cреди рядов (1) (2) (3) укажите сходящиеся абсолютно
(1)
,
(2)
,
(3)
A) (1), (2)
16. Cреди рядов (1) (2) (3) укажите сходящиеся абсолютно
(1)
,
(2)
,
(3)
A) (1), (2)
17. Cреди рядов (1) (2) (3) укажите сходящиеся абсолютно
(1)
,
(2)
,
(3)
A) (1), (2), (3)
18. Cреди рядов (1) (2) (3) укажите расходящиеся ряды
(1)
,
(2)
,
(3)
A) (3), (2)
19. Cреди рядов (1) (2) (3) укажите расходящиеся ряды
(1)
,
(2)
,
(3)
A) (3)
20. Cреди рядов (1) (2) (3) укажите расходящиеся ряды
(1)
,
(2)
,
(3)
A) (2)
1. Cреди рядов (1) (2) (3) укажите сходящиеся абсолютно
(1)
,
(2)
,
(3)
A) (1), (2)
2. Cреди рядов (1) (2) (3) укажите сходящиеся ряды
(1)
,
(2)
,
(3)
A) (2)
3. Cреди рядов (1) (2) (3) укажите сходящиеся ряды
(1)
,
(2)
,
(3)
A) (1)
4. Cреди рядов (1) (2) (3) укажите сходящиеся ряды
(1)
,
(2)
,
(3)
A) (2)
5. Исследовать сходимость ряда
A) сходится абсолютно
6. Исследовать сходимость ряда
A) расходится
7.
Исследуйте
ряд
на сходимость с помощью предельного
признака сравнения. Укажите параметр
p
сравниваемого ряда с рядом Дирихле
.
A) сходится р=5
8.
Исследуйте
сходимость ряда
A) расходится
9.
Исследуйте
сходимость ряда
A) сходится
10. Исследуйте сходимость ряда
A) сходится условно
11. Исследуйте сходимость ряда
A) сходится абсолютно
12. Исследуйте сходимость ряда
A) расходится
13. Исследуйте сходимость ряда
A) сходится абсолютно
14. Исследуйте сходимость ряда
A) сходится условно
15.
Исследуйте
сходимость ряда
A) расходится
16. Исследуйте сходимость ряда
A) сходится условно
17. Исследуйте сходимость ряда
A) сходится абсолютно
18.
Исследуйте
сходимость ряда
A) сходится
19. Исследуйте сходимость ряда
A) сходится условно
20.
Исследуйте
сходимость ряда
A) сходится абсолютно
1.
Исследуйте
сходимость ряда
A) сходится абсолютно
2.
Исследуйте
сходимость ряда
A) сходится условно
3.
Дан
общий член функционального ряда Un
(x).
Un
(x)=
(-1)
.
Найдите U3 (x)
A)
U3 (x) = -
4.
Дан
общий член функционального ряда Un(x).
Un(x)=(-1)
.
Найдите
U4 (x)
A)
U4 (x)=-
5.
Дан
общий член функционального ряда Un
(x).
Un
(x)=
.
Найдите
U2 (x).
A)
U2 (x)=
.
B6.
Дан
общий член функционального ряда Un
(x).
Un(x)=(-1)
,
Найдите U5
(x)
A)
U5(x)=
,
7.
Дан
общий член функционального ряда Un
(x).
Un(x)=(-1)
.
Найдите
U2 (x)
A)
8.
Дан
общий член функционального ряда Un
(x).
Un
(x)=
(-1)
,
Найдите U4
(x)
A)
,
9.
Функциональный
ряд
в точке
x=
имеет
вид
A)
10.
Функциональный
ряд
в точке
x=2/3
имеет
вид
A)
11.
Функциональный
ряд
в точке
x=
- 5
имеет вид
A)
B12.
Функциональный
ряд
в точке x=-2
имеет вид
A)
13.
Функциональный
ряд
в точке x=-1
имеет
вид
A)
14.
Функциональный
ряд
точке x=0
имеет вид
A)
15.
Коэффициенты
степенного ряда
n
имеют вид
A)
3n
Тестовые вопросы по дисциплине
«Операционное исчисление »
16.
Изображение
функции
имеет вид:
A)
17.
Изображение
функции
имеет вид:
A)
18.
Изображение
функции
имеет вид:
A)
19.
Свертка
функции
без вычисления интеграла имеет вид:
A)
B20.
Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
1. Решение задачи Коши дифференциального уравнения с начальными условиями операторным методом, является функция:
A)
2.
Изображение
функции
есть выражение:
A)
3.
Изображение
функции
есть выражение:
A)
4.
Изображение
функции
есть выражение
A)
5.
Свертка
функции
без вычисления интеграла имеет вид:
A)
6.
Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
7. Решением задачи Коши дифференциального уравнения с начальными условиями , операторным методом является функция:
A)
8.
Изображение
функции
есть
выражение:
A)
9.
Изображение
функции
есть
выражение:
A)
10.
Изображение
функции
есть
выражение:
A)
11.
Свертка
функции
без вычисления интеграла имеет вид:
A)
12.
Решением
задачи Коши дифференциального уравнения
с начальными условиями
,
операторным методом является функция:
A)
13.
Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
14.
Изображение
функции
есть выражение:
A)
15.
Изображение
функции
есть выражение:
A)
16.
Изображение
функции
имеет вид:
A)
17.
Изображение
функции
имеет вид:
A)
18.
Оригинал
функции
имеет вид:
A)
19.
Свертка
функции
без вычисления интеграла имеет вид:
A)
20.
Операторное
уравнение дифференциального уравнения
,
удовлетворяющее начальному условию
имеет вид:
A)
1.
Решением
задачи Коши
,
удовлетворяющем начальному условию
,
операторным методом, где изображение
является функция:
A)
2.
Изображение
функции
имеет вид:
A)
3.
Изображение
оригинала
имеет вид:
A)
4.
Изображение
функции
имеет вид:
A)
5.
Изображение
функции
имеет вид:
A)
6.
Оригинал
функции
имеет вид:
A)
7.
Свертка
функции
без вычисления интеграла имеет вид:
A)
8.
Операторное
уравнение дифференциального уравнения
,
с начальным условием
имеет вид:
A)
9.
Решением
задачи Коши дифференциального уравнения
,
,
операторным методом, где изображение
является:
A)
10.
Изображение
функции
имеет вид:
A)
11.
Изображение
функции
имеет вид:
A)
12.
Изображение
функции
имеет вид:
A)
13.
Оригинал
функции
имеет вид:
A)
14.
Свертка
функции
без вычисления интеграла имеет вид:
A)
15.
Операторное
уравнение дифференциального уравнения
,
с начальным условием
имеет вид:
A)
16.
Решением
задачи Коши:
,
операторным методом, является функция:
A)
17.
Изображение
функции
имеет вид:
A)
18.
Изображение
функции
имеет вид:
A)
19.
Изображение
функции
имеет вид:
A)
20.
Оригинал
функции
имеет вид:
A)
1.
Свертка
функции
без вычисления интеграла имеет вид:
A)
2.
Операторное
уравнение дифференциального уравнения
с начальным условием
имеет вид:
A)
3.
Решением
задачи Коши дифференциального уравнения
с
начальным условием
,
операторным методом, является функция:
A)
4.
Изображение
функции
имеет вид:
A)
5.
Изображение
функции
имеет вид:
A)
6.
Изображение
оригинала
по теореме об интегрировании оригинала
имеет вид:
A)
7.
Изображение
функции
имеет вид:
A)
8.
Оригинал
функции
имеет вид:
A)
9.
Свертка
функции
без вычисления интеграла имеет вид:
A)
10.
Операторное
уравнение дифференциального уравнения
с начальным условием
имеет вид:
A)
11.
Решением
задачи Коши:
с начальным условием
операторным методом, является функция:
A)
12.
Изображение
оригинала
имеет вид:
A)
13.
Операторное
уравнение дифференциального уравнения
с начальным условием
имеет вид:
A)
14.
Решением
задачи Коши:
,
операторным методом, является функция:
A)
15.
Изображение
функции
имеет вид:
A)
16.
Изображение
оригинала
имеет вид:
A)
17.
Изображение
функции
по теореме об интегрировании изображения
имеет вид:
A)
18.
Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
19. Решением задачи Коши: , операторным методом, является функция:
A)
20.
Изображение
функции
имеет вид:
A)
1.
Изображение
функции
имеет вид:
A)
2.
Изображение
оригинала
по теореме об интегрировании оригинала
имеет вид:
A)
3.
Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
4. Решением задачи Коши: , при операторным методом является функция:
A)
5.
Изображение
функции
имеет вид:
A)
6.
Изображение
функции
имеет вид:
A)
7.
Изображение
функции
по теореме интегрирования изображения
имеет вид:
A)
8.
Результатом
интегрирования оригинала
является изображение:
A)
9.
Оригинал
изображения
есть функция:
A)
10.
Свертка
функции
без вычисления интеграла имеет вид:
A)
11.
Операторное
уравнение дифференциального уравнения
с начальным условием
имеет вид:
A)
12.
Решением
задачи Коши
,
при
операторным методом является функция:
A)
13.
Изображение
функции
имеет вид:
A)
14.
Изображение
функции
имеет вид:
A)
15.
Результатом
интегрирования оригинала
является изображение:
A)
16.
Изображение
функции
имеет вид:
A)
17.
Оригинал
изображения
имеет вид:
A)
18.
Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
19.
Решением
задачи Коши
;
операторным методом, является функция:
A)
20.
Изображение
оригинала
имеет вид:
A)
1. Изображение
оригинала
имеет вид:
A)
2. Изображение
оригинала
имеет вид:
A)
3. Результатом
интегрирования оригинала
является изображение:
A)
4. Оригинал
функции
имеет вид:
A)
5. Свертка
функции
без вычисления интеграла имеет вид:
A)
6. Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
7. Решением
задачи Коши
;
операторным методом, является функция:
A)
8. Изображение
оригинала
имеет вид:
A)
9. Изображение
оригинала
имеет вид:
A)
10. Изображение
оригинала
имеет вид:
A)
11. Оригинал
функции
имеет вид:
A)
12. Свертка
функции
без вычисления интеграла имеет вид:
A)
13. Операторное
уравнение дифференциального уравнения
с начальными условиями
имеет вид:
A)
14. Решением
задачи Коши
;
операторным методом, является функция:
A)
15. Изображение
оригинала
имеет вид:
A)
МОДУЛЬ 5 «Элементы теории вероятностей и математической статистики»
16. Случайная величина подчинена закону
xi |
4 |
8 |
10 |
pi |
0.25 |
0.45 |
? |
Чему равна вероятность наступления события х3=10?
A) 0.3