3.3 Описание построения картины эвольвентного зацепления

Построение картины эвольвентного зацепления проводим в соответствии со следующим алгоритмом.

1. Намечаем центры зубчатых колес O₁ и O₂, отложив на межосевой линии в масштабе _L расстояние a_W. Дальнейшее построение ведем в выбранном масштабе. Межосевую линию проводим так, чтобы она начиналась в верхнем правом углу, а заканчивалась на расстоянии в ¼ высоты листа от нижнего левого угла. Исходя из соображений, что на чертеже должно быть a_W  900…930 мм, принимаем масштабный коэффициент 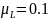м/мм.

2. Наносим на чертеж начальные окружности, определив тем самым положение полюса зацепления Р.

3. Через точку P проводим перпендикуляр к O₁O₂ методом засечек.

4. Из точек O₁, O₂ проводим лучи под углом _сб к отрезку O₁O₂. Для более точного построения угла проводим из точки P вдоль перпендикуляра отрезки PH₁ и PH₂ равные , . Точки H₁ и H₂ соединяем с точками O₁ и O₂.

5. Наносим на чертеж основные окружности. Точки их пересечения с лучами O₁H₁ и O₂H₂ обозначим соответственно N и M. Проводим линию NM  теоретическую линию зацепления. Точка P обязательно должна располагаться на линии NM, в противном случае даже при малейшем расхождении нужно искать ошибку.

6. Посредством перекатывания линии зацепления по основным окружностям 1-го и 2-го колес получаем эвольвентные профили зубьев.

Алгоритм построения эвольвенты:

1) Отрезок PN разбиваем на несколько частей (4 или 6) равной длины P1=12=23=34=…

2) Из точки N по дуге основной окружности откладываем дуги 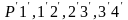и т. д., так чтобы 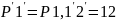и т. д. (отрезки откладываем циркулем в предположении, что длина хорды равна длине дуги окружности)

3) Через точки 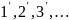проводим лучи, характеризующие положение прямой в процессе ее перекатывания по основной окружности. 4) Из точек откладываем на проведенных лучах отрезки равные соответственно отрезкам .

5) Соединяя точки 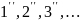получаем эвольвенту профиля зуба.

Аналогично строим эвольвенту и для второго колеса.

7. Наносим на чертеж все оставшиеся окружности зубчатого зацепления (окружности головок и впадин зубьев, делительные окружности).

8. Находим ось симметрии зуба, зная его толщину по начальной окружности (для этого делим S_Н на 4 части и откладываем их циркулем по дуге начальной окружности). Имея положение оси симметрии зуба и его толщины по другим окружностям, строим эвольвенту его другой стороны.

В случае, когда ножка зуба на участке от основной окружности до окружности впадин представляет собой участок радиуса, соединяющего начало эвольвенты (точка P) с центром колеса, радиус закругления =0,2m.

9. С учетом шага t строим профили еще двух зубьев для каждого колеса (справа и слева). Делим шаг на 4…6 частей и откладываем их по делительной окружности при помощи циркуля, тем самым получаем положения осей симметрии. При построении зубьев можно использовать метод симметрии, перенося толщины зубьев с имеющегося зуба циркулем.

10. Находим практическую линию зацепления. Практическая линия зацепления ab отсекается на теоретической линии зацепления NM окружностями головок зубчатых колес.

11. Находим дугу зацепления. Через точки a и b пунктирными линиями проводим эвольвенты зубьев при входе в зацепление и при выходе из него. Расстояние между эвольвентными профилями зубьев по начальной окружности является дугой зацепления (дуги ce и fd).

12. Отмечаем рабочие участки профилей зубьев. Для нахождения рабочего участка зуба надо найти на нем точки сопряженные с точками a и b. Для этого, например, на первом колесе проводим дуги окружностей радиусами O₁a и O₁b до пересечения с профилем зуба и получаем точки A₁ и B₁ соответственно. Отрезок эвольвенты A₁B₁  рабочий участок профиля зуба первого колеса.

13. Рассчитывается коэффициент перекрытия через практическую линию зацепления

Сравнивая его со значением коэффициента перекрытия, вычисленного ранее, получаем, что отклонение составляет 0 %.