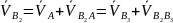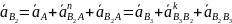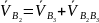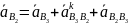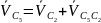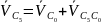1.3 Кинематический анализ механизма методом векторных диаграмм

1.3.1 Векторные уравнения для построения планов скоростей и ускорений

Векторные уравнения для построения планов скоростей и ускорений представлены в таблице 1.1.

В таблице 1.1 приняты следующие обозначения:

I – точка принадлежащая внутренней кинематической паре группы Ассура;

J – точка принадлежащая внешней кинематической паре группы Ассура;

I – уравнение I-го типа (теорема о сложении скоростей или ускорений при плоском движении);

II – уравнение II-го типа (теорема о сложении скоростей или ускорений при сложном движении).

Таблица 1.1 – Векторные уравнения для построения планов скоростей и ускорений

Группа Ассура	I	J	Тип уравнения	Теорема	Уравнение
	B2	A	I
		B3	II
	C5	C2	II
		C0	II

1.3.2 Построение планов скоростей

Проведем анализ векторных уравнений для построения планов скоростей представленных в таблице 1.1.

, (1)

. (2)

– скорость точки B₂. Является искомой величиной.

– скорость точки A. Этот вектор направлен перпендикулярно отрезку OA. Его величина для всех положений механизма равна

.

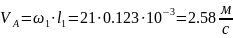– скорость точки B₂ при вращении звена вокруг точки А. Этот вектор направлен перпендикулярно отрезку BA. После нахождения значения этого вектора угловую скорость 2-го звена рассчитаем по формуле

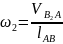, (3)

где ; AB – длинна отрезка AB, измеренная на плане механизма.

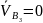– скорость точки B₂;

– скорость точки B2 относительно B3. Этот вектор направлен параллельно отрезку AB.

– скорость точки С₅. Является искомой величиной.

– скорость точки С₂. На плане скоростей направление и величина этого вектора определяется по теореме подобия.

– скорость точки С₅ относительно С₂. Этот вектор направлен параллельно отрезку BC.

– скорость точки C₀.

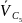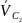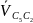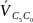– скорость точки С₅ относительно C_0. Этот вектор направлен параллельно линии τ-τ.

Построим план скоростей. Построение ведем в соответствии с векторными уравнениями (1) и (2).

Расчеты по теореме подобия для различных положений механизма представлены в таблице 1.2.

Таблица 1.2. – Расчеты по теореме подобия для планов скоростей

	1	2	3	4	5	6	7
AB	75	111	125	110	72	45	75
AC	96	89	85	90	96	85	96
a b2	0	76	100	73	7	100	0
ac2	0	61	68	60	9	189	0

На плане скоростей вектор будем изображать отрезком 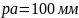. В этом случае масштаб планов скоростей будет равен

.

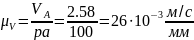Рассчитанные значения скоростей для различных положений механизма представлены в таблице 1.3, а значения угловых скоростей в таблице 1.5.

Таблица 1.3 – Значения скоростей для различных положений механизма

	1	2	3	4	5	6	7
pb2, мм	100	65	2	68	100	6	100
VB2, м/с	2.58	1.68	0.05	1.76	2.58	0.16	2.58
pa, мм	100	100	100	100	100	100	100
VA, м/с	2.58	2.58	2.58	2.58	2.58	2.58	2.58
ab2, мм	0	76	100	73	7	100	0
VB2A, м/с	0.00	1.96	2.58	1.89	0.18	2.58	0.00
pb3, мм	0	0	0	0	0	0	0
VB3, м/с	0.00	0.00	0.00	0.00	0.00	0.00	0.00
b3b2, мм	100	65	2	68	100	6	100
VB2B3, м/с	2.58	1.68	0.05	1.76	2.58	0.16	2.58
pc5, мм	0	64	68	72	10	189	0
VC5, м/с	0.00	1.65	1.76	1.86	0.26	4.88	0.00
pc2, мм	100	89	68	96	100	189	100
VC2, м/с	2.58	2.30	1.76	2.48	2.58	4.88	2.58
c2c5, мм	100	45	2	45	105	12	100
VC5C2, м/с	2.58	1.16	0.05	1.16	2.71	0.31	2.58
pc0, мм	0	0	0	0	0	0	0
VC0, м/с	0.00	0.00	0.00	0.00	0.00	0.00	0.00
c0c5, мм	0	64	68	72	10	189	0
VC5C0, м/с	0.00	1.65	1.76	1.86	0.26	4.88	0.00

Таблица 1.4 – длины отрезков AB для различных положений механизма

	1	2	3	4	5	6	7
AB, мм	75	111	125	110	72	45	75
lAB, м	0,23	0,34	0,38	0,34	0,22	0,14	0,23

Таблица 1.5 – значения угловых скоростей для различных положений механизма

	1	2	3	4	5	6	7
ω2, рад/с	0,00	5,75	6,72	5,57	0,82	18,67	0,00