Питання для самоперевірки.
Дайте означення матриці та її розміру. Які існують різновиди матриць?
За якими правилами матрицю можна помножити на дійсне число, знайти алгебраїчну суму та добуток матриць?
Які елементи утворюють головну та неголовну діагоналі квадратної матриці?
Дайте означення визначника n – го порядку.
За якими правилами обчислюють визначники 2 та 3 – го порядків?
Сформулюйте властивості визначника.
Як визначають та позначають обернену матрицю до матриці А?
Дайте означення рангу матриці та вкажіть методи його заходження.
Розкажіть про відомі вам способи знаходження оберненої матриці.
Розповісти про метод Жордана – Гауса.
Задачі для самостійного розв’язання.
Обчислити
визначники:
а) 2 -4 б) 5 1 6 в) 3 -1 4
-1 5 ; 1 6 5 ; -2 0 3 ;
6 5 1 1 3 4
г) 1 0 2 3 д) 1 1 1 1 е) 6 -5 8 4
2 0 2 0 2 1 3 4 9 7 5 2
3 1 4 5 ; 4 1 9 16 ; 7 5 3 7 .
5 0 0 0 8 1 27 64 -4 8 -8 -8
2.Знайти ранг матриці:
а ) 2 -3 5 7 б) 1 0 3 -2 4 в) 1 2 3 -1 -4
4 -6 2 3 ; 2 1 1 -2 1 ; 2 3 4 -2 1
2 -3 -11 -15 -1 -1 2 0 3 -1 -1 -1 1 -5 .
-2 0 2 -5 -3
3. Знайти обернену матрицю до заданої матриці:
а) 1 2 -1
б) 2 1 0 в) 3 4
2 1 3 ; 3 0 5 ; 5 7
3 1 1 7 6 4
4. Матричним методом розв’язати системи:
а)
3х + 2у = 7 б) 2х – 3у + z
= 0
4х – 5у = 40 ; х + 5у – 4z = 0
4х
+ у – 3z
+ 4 = 0
З найти АВ, якщо: а) А = 1 2 В = -1 1 2
-1 1 , 2 1 5 ;
б) А = 3 -2 В = 3 4
5 -4 , 2 5
Знайти матрицю А + 3В – С, якщо:
А = 3 5 В = 2 -1 С = 9 2
1 -2 , -1 2 , -2 4 .
Розв’язати методом Жордана – Гаусса:
а) 2х1 + х2 - х3 - х4 = 2 б) 2х1 + 5х2 – 8х3 = 8
4х1 + х3 – 7х4 = 3 ; 4х1 + 3х2 – 9х3 = 9
2х2 – 3х3 + х4 = 1 2х1 + 3х2 – 5х3 = 7
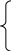х1
+ 8х2
– 7х2
= 12 .