8. Матричний спосіб розв’язання систем (слар)

Нехай задана система:

а₁₁х + а₁₂y + a₃₇z = b₁

a₂₁х + a₂₂y + a₂₃z = b₂

a₃₁x + a₃₂y + a₃₃z = b₃

Позначимо:

а₁₁ а₁₂ а₁₃ х b₁

А = а₂₁ а₂₂ а₂₃ Х = y B = b₂

а₃₁ а₃₂ а₃₃ z b₃

В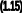 икористовуємо дії з матрицями, отримуємо:

A*X = B - матричний запис системи

Домножемо рівність (1.15) на А^-1:

A^-1*АX = A^-1*B

Е*Х = А^-1*В

X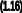 = A^-1*B

Таким чином, (1.16) – розв’язок системи записаний за допомогою матриць.

Приклад 16.

х – 2y + 3z = 2 1 -2 3 2 х

2x + y – 4z = 4 A = 2 1 -4 B = 4 X = y

3x – y + z = 8 3 -1 1 8 z

А*Х = В

X = A^-1*B

1 -2 3

det A = 2 1 -4 = 1 + 24 – 6 – 9 + 4 – 4 = 10

3 -1 1

А₁₁ = -3 А₁₂ = -14; А₁₃ = -5; А₂₁ = -1; А₂₂ = -8;

А₂₃ = -5; А₃₁ = 5; А₃₂ = 10; А₃₃ =5;

-3 -1 5

А^-1 = -14 -8 10

-5 -5 5

x -3 -1 5 2

x = y = -14 -8 10 * 4 =

z -5 -5 5 8

-6 -4 +40 30 3 x = 3; 3

-28 -32 +80 = * 20 = 2 ; y = 2; X = 2

-10 -20 +40 10 1 z = 1; 1

9. Ранг матриці

Рангом матриці називається максимальне число її лінійно незалежних рядків (стовпців).

Рядки матриці називаються лінійно незалежними, якщо їх лінійна комбінація дорівнює нулю.

Λ₁*l₁+ Λ₂*l₂+…+Λ_n*l_n = 0

При умові, що Λ₁ = Λ₂ =… = Λ_n=0

Якщо формула справедлива при умові Λ_i ≠ 0, то рядки називають лінійно залежними, наприклад, Λ₃ ≠ 0, тоді можна рядок l₂ виразити через інші рядки.

П риклад17.

1 2 -1 3 l₁

A = 1 -3 2 1 l₂

-1 4 3 -2 l₃

Λ₁*l₁ + Λ₂*l₂ + Λ₃*l₃=0

l₁ + l₂ - l₃ = 0

l₃ = l₁ + l₂

l₂ = l₃ – l₁

Три рядки з даної матриці є лінійно залежними.

Лінійна залежність означає, що одне можна виразити через інше.

Λ ₁*l₁ + Λ₂*l₂ = 0

0*l₁ + 0*l₂ = 0 лінійно незалежні

r_A(rang A) = 2 (рядки)

Елементарні перетворення, які не змінюють рангу матриці:

1. Множення рядка (стовбця) матриці на число відмінне від нуля;

2. Множення рядка (стовбця) матриці на число відмінне від нуля і додавання до іншого рядка (стовбця).

Ці перетворення використовуємо для перетворення елементів матриці в нулі і одинички.

Правило знаходження рангу:

1. Використовуючи елементарні перетворення, перетворюємо елементи матриці в нулі і одиниці до тих пір, поки в кожному рядку (стовбці) буде не більше однієї одиниці;

2. Число одиниць дорівнює числу незалежних рядків, а отже рангу матриці.

Приклад 18.

3 -2 4 2 -3 0 4 1 -7 -3 0 4 1 -7 -3 0 4 1 -7 -3

1 -2 1 3 0 1 -2 1 3 0 1 -2 1 3 0 1 0 0 0 0

А = 0 -2 1 0 3 ~ 0 -2 1 0 3 ~ 0 -2 1 0 3 ~ 0 -2 1 0 3 ~

4 -4 5 5 -3 0 4 1 -7 -3 0 0 0 0 0 0 0 0 0 0

1 -4 2 3 3 0 -2 1 0 3 0 0 0 0 0 0 0 0 0 0

0 6 0 -7 -6 0 6 0 -7 -6 0 6 0 -7 -6 0 1 0 0 0

1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0

~ 0 -2 1 0 3 ~ 0 0 1 0 0 ~ 0 0 1 0 0 ~ 0 0 1 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1,2,3 – й рядки лінійно незалежні.

0 4 1 -7 -3 l₁ 0 4 1 -7 -3 0 6 0 -7 -6

1 0 0 0 0 l₂ 1 0 0 0 0 1 0 0 0 0

А = 0 -2 1 0 3 l₃ ~ 0 -2 1 0 3 ~ 0 0 1 0 0

0 4 1 -7 -3 l₄ 0 0 0 0 0 0 0 0 0 0

0 -2 1 0 3 l₅ 0 0 0 0 0 0 0 0 0 0

1* l₁ + 1* l₂ + 0* l₃ – 1* l₄ + 0* l₅ = 0 – лінійна комбінація рядків матриці А. Всі 5 рядків лінійно залежні.

Максимальне число лінійно незалежних рядків дорівнює 3. Тому ранг А = 3.