Тема 7. Числові та степеневі ряди.

1.Означення знакододатнього числового ряду, сума ряду, збіжність ряду. 2.Необхідна ознака збіжності числового ряду .

3.Достатні ознаки збіжності числового ряду:

3.1.Ознака Даламбера.

3.2. Ознаки порівняння.

3.3 . Радикальна ознака Коші

3.4. Інтегральна ознака Коші

4.Поняття про знакопочережні числові ряди. Ознака Лейбнійца.

5.Степеневі ряди.Ознака Абеля.

6.Ряди Маклорена та їх застосування до наближених обчислень визначених інтегралів.

Числовим рядом –називають суму членів числової послідовності записують

а₁+а₂ +...+ а_n = аn (7.1)

_+... (7.2)

Сумою ряду (7.1) називають S= Sn.

Сума n членів ряду (7.1) має вигляд: Sn = а₁+а₂ +...+ а_{n .}

Знайдемо для ряду (7.2) : Sn= S= (1- ) =1

Ми отримали, що сума

Ряд, який, має сумою скінчене число називають збіжним рядом. В протилежному випадку – розбіжним.

Теорема 1. Необхідна ознака

Якщо ряд 7.1 збіжний то обов’язково виконується умова 7.4 lim a_n=0 (7.4). Умова 7.4 тільки необхідно n . Тому у випадку коли вона не виконується. Той ряд обов’язково розбіжний.

Приклад 1.

Дослідити на збіжність

lim

Тому ряд розбіжний

Приклад 2.

Питання збіжності ряду залишається відкритим

Теорема 2. Ознака Даламбера

Якщо для числового ряду 13.1 де p  число

Якщо:

1. p<1, то ряд збіжний

2. p>1, то ряд розібжний

3. p=1, ? то питання залишається відкритим

n!=

6!=123456=240

(3n+1)!=123…3n(3n+1)=(3n)!(3n+1)

Приклад 3.

це дорівнює ряд збіжний

Теорема №3. Радикальна ознака Коші

Якщо для ряду 7.1

Якщо:

1. q<1,то ряд збіжний

2. q>1,то ряд розбіжний

3. q=1,? ? то питання залишається відкритим

Приклад 4.

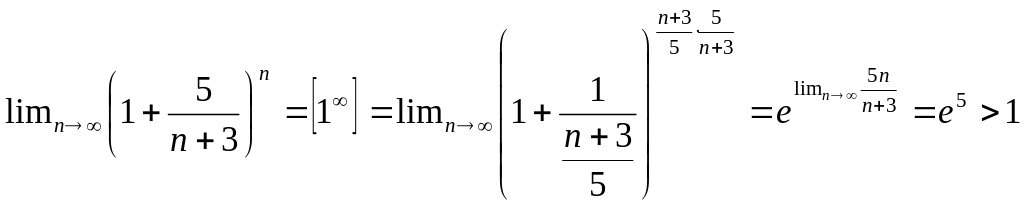
 ряд розбіжний

Теорема 4. Інтегральна ознака Коші

Якщо для ряду 7.1 інтеграл  збіжний то ряд збіжний.

Якщо інтеграл розбіжний то ряд розбіжний.

Приклад 5.

Інтеграл збіжний, тому ряд збіжний

Теорема 5. Порівняльна ознака

Якщо для рядів (7.5)

Виконується умова , то ряди ведуть себе однаково

В ролі ряду 7.5 беремо ряд збіжність якого наперед відома. Наприклад узагальнений гармонічний ряд, >1  збіжний;

 1  розбіжний;

Приклад 6 (З прикладу 2)

Так, як ряд еталон збіжний то ряд збіжний.

Поняття про знакопочережний числовий ряд. Ознака Лейбнійца

Означення 1. Ряд, члени якого почережно мають додатний та від'ємний знаки, називають знакопочережним. Такий ряд можна записати, наприклад, у вигляді

(14).

Означення 2. Знакопочережний ряд називають збіжним абсолютно, якщо збігається додатний числовий ряд складені тій з абсолютних величин знакопочережного ряду (14).

Якщо ряд, складений з абсолютних величин членів ряду (14) розбігається, а знакопочережний ряд збігається, то кажуть, що ряд (14) збігається неабсолютно або умовно.

Абсолютну збіжність знакопочережного ряду досліджують з ви­користанням достатніх ознак збіжності додатних числових рядів. Неабсолютну збіжність знакопочережного ряду досліджують з ви­користанням ознаки Лейбніца.

Ознака Лейбніца. Якщо абсолютні величини знакопочереж­ного ряду монотонно спадають, тобто

U₁>U₂>U₃>…>U_n>…

і границя його загального члена дорівнює нулю при тобто виконується умова

тоді знакопочережний ряд збігається, причому його сума S обов'язково менше першого члена ряду.

Якщо замінити суму цього ряду S його частковою сумою S_m,

тоді абсолютна величина похибки R_m буде менше першого від­кинутого члена ряду, тобто |R_m| <U_m+1

Остання оцінка використовується у наближених обчисленнях.

Приклад №7. Дослідити збіжність знакопочережних рядів:

Разв 'язування. а) Складемо ряд з абсолютних величин за­даного знакопочережного ряду ( — довільне число):

Порівняємо цей ряд із збіжним узагальненим гармонічним рядом

Кожний член ряду (15) менше або дорівнює відповідному члену ряду (16) тому, що

Згідно з ознакокою порівняння ряд (15) збігається, а це озна­чає, що заданий знакопочережний ряд

а) збігається абсолютно; b) У цьому випадку ряд, складений з абсолютних величин

 розбіжний гармонічний ряд, тому ряд

 абсолютно не збігається. Для дослідження його неабсолютної збіжності треба застосувати ознаку Лейбніца. У даному випад­ку обидві умови ознаки Лейбніца виконуються:

Тому знакопочережнии ряд b) збігається неабсолютно.

c) У цьому випадку не виконується необхідна умова збіж­ності числового ряду тому, що

Отже, ряд  розбіжний.

Означення 3.

Степеневим рядом називають ряд вигляду

(1)

або

(2)

де - дійсні числа, які називають коефіцієнтами степеневого ряду, - деяке постіне число.

Теорема Абеля.

Якщо ряд (1) збігаеться при , то він збігаеться абсолютно для усіх , що задовольняють нерівність

<

Якщо ряд (1) розбігаеться при , то він розбігаеться для усіх , які задовольняють нерівність

>

Наслідок.

Якщо степеневий ряд (1) збігаеться при , то цей ряд збігаеться в інтервалі .

Означення 7.

Додатнє число , таке, що при < степеневий ряд збігаеться, а при > ряд розбігаеться, називають радіусом збіжності степеневого ряду. Інтервал називають інтервалом збіжності цьго ряду.

Радіус збіжності степеневого ряду знаходять за формулами

або

Теорема.

Якщо в деякому інтервалі, що містить точку , функція має похідні будь-якого порядку, які задовольняють умовам , >0 для усіх із цього інтервала та будь-якого , то функція для усіх із цього інтервала розкладаеться у степеневий ряд вигляду:

(3)

Степеневий ряд (3) по степенях називають рядом Тейлора функції . При =0 одержуемо степеневий ряд по степенях вигляду:

(4)

Цей ряд називають рядом Маклорена функції .

Розклад у ряд Маклорена функцій, що використовуються найчастіше:

1. ,

2. < 1

3.

4.

5.

Розклад функцій у ряд маклорена використовується для знаходження наближеного значення функції, визначеного інтеграла, розв’язування диференційних рівняннь.

Для обчислення наближеного значення функції в точці діють так:

1. розкладають у степеневий ряд;

2. підставляють у розклад замість число і одержують , як суму числового ряду;

3. залишають у розкладі перші членів, а інші відкидають, тобто одержують наближене значення

де - часткова сума членів числового ряду;

4. оцінюють похибку знайденого наближеного числового значення . Якщо числовий ря д знакопостійний, тоді ряд, складений з відкинутих членів, порівнюють з рядом збіжної геометричної прогрессії. У випадку знакопочережного числового ряду застосовують ознаку Лейбніца, за якою абсолютна величина похибки буде меншн першого відкинутого члена ряду, тобто

<

Приклад 6.

Обчислити використовуючи три члена розкладу функції у степеневий ряд.

Розв’зування. Згідно з розкладом 3 функцій у ряд Маклорена маємо:

У нашому випадку , тому можна підставити у розклад замість число 0.6 і одержати знакопочережний числовий ряд

Обмежуючись трьома членами ряду за умовою прикладу одержимо:

Абсолютна величина похибки оцінюється так: