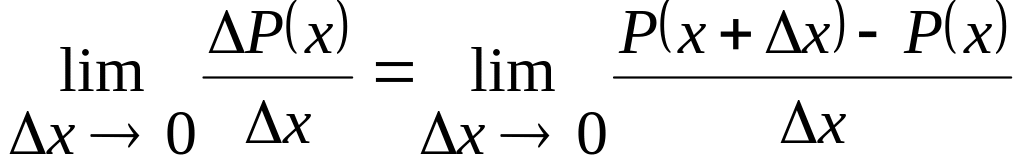4 Властивості:

1. Функція у =f(x), визначена і неперервна в обмеженій замкненій області D, є обмеженою.

Зауваження. Властивість не виконується, якщо область D відкрита. неперервна в інтервалі (0, 1), але вона в цьому інтервалі необмежена.

1. Якщо функція y = f(x) неперервна в точці а і f(a) 0, то функція в достатньо малому околі точка а зберігає знак.

2. Якщо функція у =f(x) визначена і неперервна на відрізку [а,b] і

f(а) < 0, f(b) > 0, то на цьому відрізку знайдеться принаймні одна точка С, в якій функція перетворюється в нуль, тобто f(C) = 0.

5

Означення 3. Пряма х = а називається вертикальною асимптотою для функції y = f(x), якщо точка х = а є точкою розриву другого роду.

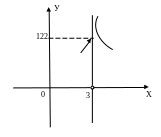
Для попередньої функції пряма х = -2 є вертикальна асимптота

х = 3 другого роду, є односторонньою вертикальною асимптотою, намалюємо ескіз графіка х = 3

Означення 4. Пряма y = kx + b називається похилою асимптотою, якщо

(8.4)

Якщо одне із чисел k або b є нескінченними, то похилої асимптоти не існує.

Приклад 6. Знайти асимптоти для функції

1. Вертикальні асимптоти:

ОДЗ:

х = -2 – точка розриву.

Дослідимо вид розриву

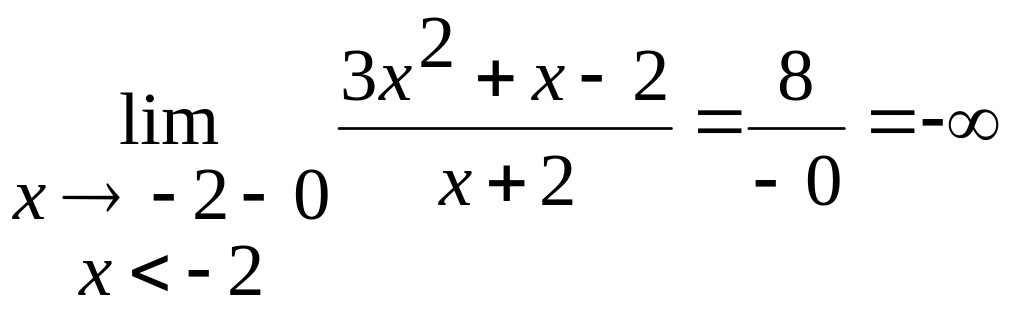
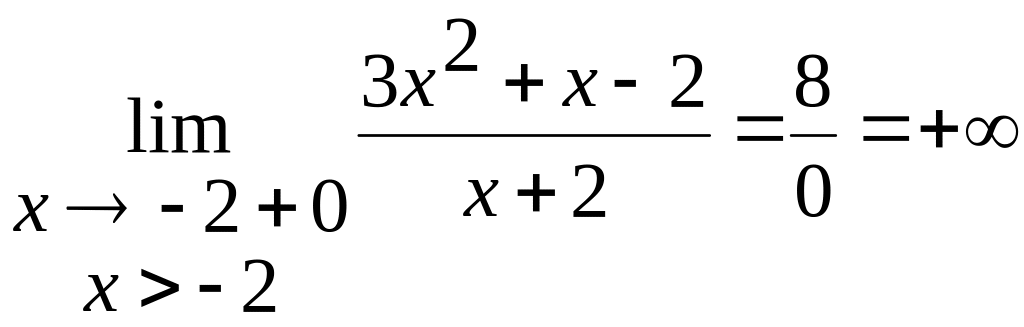
Розрив другого роду, тому пряма х = -2 є вертикальна асимптота.

2. Похилі асимптоти.

y = kx + b

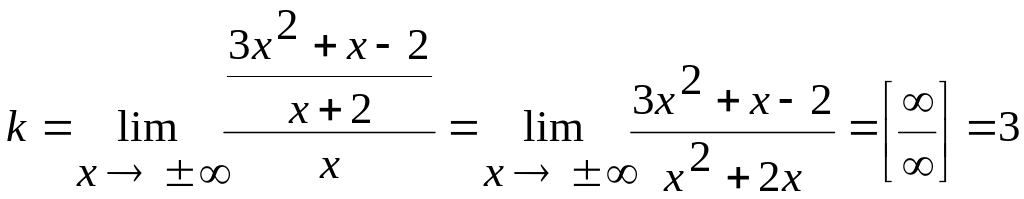
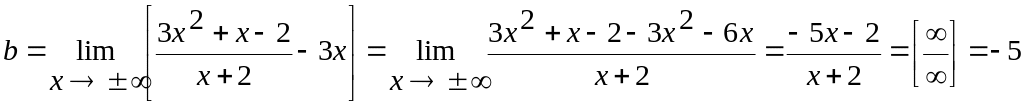
у = 3х – 5

Зауваження: якщо k=0, то у=b – горизонтальна асимптота.

Питання для самоперевірки

11. Дайте означення неперервності функції в точці.

12. Дайте означення точки розриву.

13. Наведіть класифікацію точки розриву.

14. Сформулюйте поняття неперервності функції на відрізку.

15. Наведіть властивості неперервних функцій.

16. Дайте означення вертикальної асимптоти.

17. Наведіть умову неперервності функції в точці.

18. За якими формулами находяться похилі асимтоти.

Завдання для самостійного розв’язання

1. Дослідити на неперевсність функції. Вказати вид розриву.

2. Знайти похилі і вертикальні асимптоти.

   1. 

   2. 

   3. 

   4. 

   5. 

   6. 

   7. 

   8. 

   9. 

Тема 9. Поняття похідної. Похідні функцій, заданих явно, неявно, параметрично.

План

1. Задачі, які привели до поняття похідної.

2. Означення похідної та її геометричний зміст.

3. Зв’язок диференційованості функції з неперервністю.

4. Основні правила диференціювання.

5. Таблиця похідних.

6. Поняття диференціала функції та його застосування до наближених обчислень. Геометричний зміст диференціалу.

7. Похідні вищих порядків.

8. Функція задана наявно та її похідна.

9. Похідна степенево-показникової функції.

10. Похідна функції, заданої параметрично.

1. Задачі, які привели до поняття похідної

Задача про швидкість прямолінійного руху.

Нехай тіло рухається прямолінійно вздовж осі Os, але нерівномірно. Тоді координата S точки буде змінюватися з часом за деяким законом, тобто S=s(t). Починаючи з деякого моменту t за час ∆t тіло пройде шлях ∆S = s(t + ∆t) – s(t). Середня швидкість за проміжок часу ∆t буде .

Середня швидкість дає лише наближене уявлення про рух в окремі моменти часу. Так, на початку проміжку ∆t тіло могло рухатися прискорено, а в кінці цього проміжку – уповільнено. Коли проміжок часу ∆t зменшується, тоді наближається до швидкості руху в момент t. Що відповідає початку проміжку ∆t .

Миттєвою швидкістю V (або швидкістю в момент t) називають границю відношення приросту шляху ∆S до приросту часу ∆t, коли ∆t →0, тобто

Миттєва швидкість V залежить від часу t, а також від вигляду функції S = S(t).

Задача про дотичну.

Нехай задана функція y = f(x). Графіком цієї функції на площині xOy буде деяка крива лінія.

Дотичною до кривої y = f(x) в точці М(х, у) називають граничне положення МТ січної ММ1, коли точка М1, рухаючись вздовж кривої до точки дотику.

Тангенс кута нахилу січної ММ1 до осі Ох буде

Із означення дотичної випливає, що її кутовий коефіцієнт є границя, до якої прямує кутовий коефіцієнт січної при необмеженому наближенні точки М1 до точки М, тобто при ∆x→0:

Задачі про маргінальні вартість, доход, прибуток.

Маргінальними витратами називають гранично можливі витрати в умовах хоча би постійного відтворення виробництва відповідної продукції. Аналогічно визначають маргінальні доходи та прибуток.

Позначимо через V(x), D(x) та Р(х) витрати, доход та прибуток виробництва х одиниць продукції. Кожна з цих величин є певною функцією кількості одиниць х виробленої продукції. Якщо підприємство збільшує випуск продукції на ∆x одиниць, то ці функції одержать приріст

∆V(x) = V(x + ∆x) – V(x)

∆D(x) = D(x + ∆x) – D(x)

∆P(x) = P(x + ∆x) – P(x)

Відношення приросту функції до ∆x характеризує приріст відповідної функції на одиницю приросту продукції, а границя цього відношення при ∆x→0 стає маргінальною. Отже:

Маргінальна вартість:

Маргінальний доход:

Маргінальний прибуток: