7 Перша чудова границя

Означення 4.При знаходженні границі виразів, що містять тригономет­ричні функції, часто використовують границю

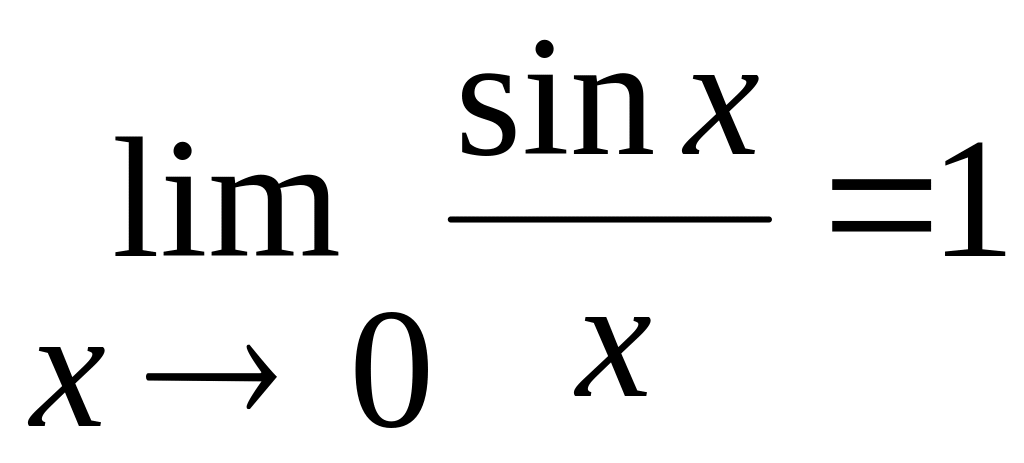, (7.2)

яку називають першою чудовою границею.

_{Для доведення рівності (8.2) побудуємо коло одиничного радіуса та кут АОВ =} х (радіан), де 0 < х < .

Побудуємо лінію сінуса ВС та лінію тангенса АВ. Із малюнка видно, що площа ΔАОВ менше площі сектора АОВ, а остання менше площі ΔОАО.

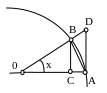
Побудуємо лінію сінуса ВС та лінію тангенса АВ. Із малюнка видно, що площа ΔАОВ менше площі сектора АОВ, а остання менше площі ΔОАD.

Площа ΔОАD дорівнює , площа сектора ОАВ дорівнює , а площа ∆ОАD дорівнює . Отже, маємо нерівності sinx < x < tgx.

При 0 < х < маємо sinx > 0, тому нерівність можна поділити на sin x. Одержимо

< <

Для обернених величин можна записати такі нерівності

cosx < < 1 (7.3)

Оскільки , то за першою ознакою існування границі змінної величини із нерівностей (8.3) одержимо

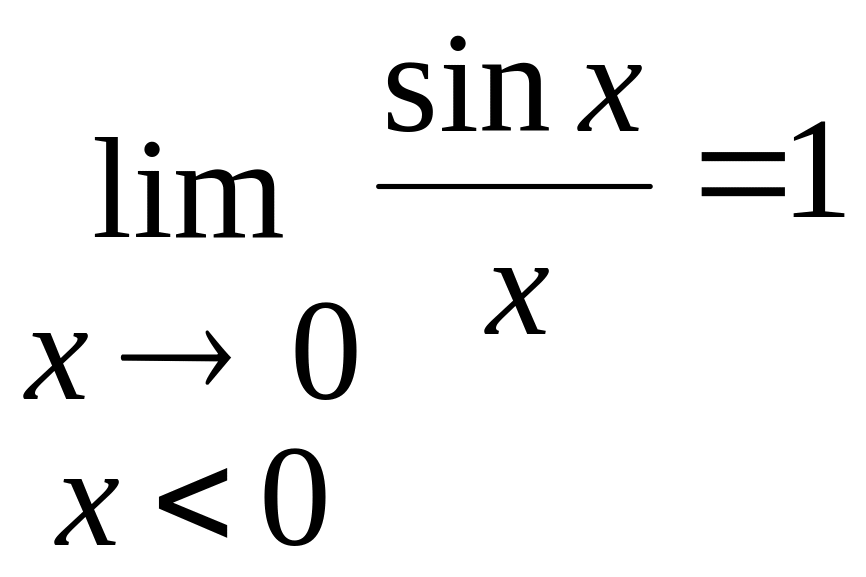(7.4)

Отже, рівність доведена для х>0. При х<0 позначимо

x = - t, t > 0, тоді

Тому, для х < 0 маємо

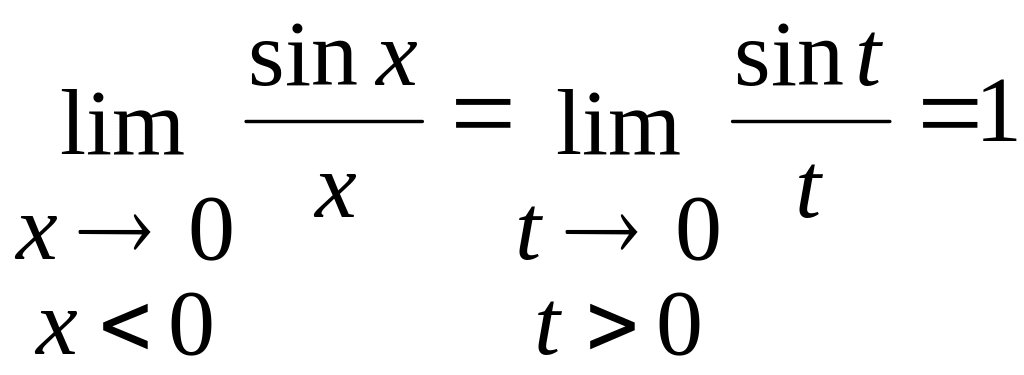(7.5)

Із рівностей (7.4) та (7.5) випливає рівність (7.2), яку треба було довести.

Приклад 3.

Застосування першої чудової границі до розкриття невизначеності у випадку тригонометричних функцій 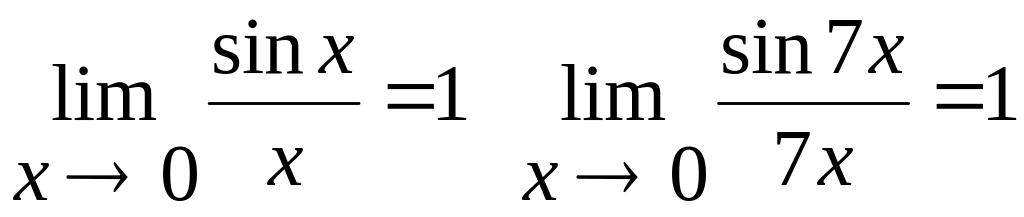- чудова.

Приклад 4.

Приклад 5.

Приклад 6.

8

Друга чудова границя.

Розглянемо послідовність та підрахуємо декілька її значень.

…

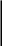^{Бачимо, що . Можна довести, що для будь -} якого n має місце нерівність яка означає, що змінна монотонно зростає. В той же час усі підраховані значення за­довольняють нерівність . Можна показати, що ця нерівність має місце для усіх значень n. Отже, змінна монотонно зростає і

залишається обмеженою зверху числом 3. Згідно з другою озна­кою існування границі змінної величини робимо висновок, що ця змінна має скінченну границю.

Означення 5. Скінченну границю послідовності називають числом е, тобто

(7.6)

Оскільки для будь-яких значень n > 1 мають місце нерівності 2 < < 3, тому число е задовольняє нерівностям 2 < е< 3.

Число е — ірраціональне, воно часто використовується в мате­матиці та економіці і дорівнює є = 2,718281....

В практичних підрахунках наближено приймають є = 2,72. Рівністю (7.6) ми визначили число е при , коли n приймає лише цілі та додатні значення. Можна довести таке твердження:

^{якщо змінна , приймаючи будь-які дійсні (раціональні та ірраціональні) додатні значення, то функція має своєю границею також число е , тобто}

(7.7)

Якщо в лівій частині рівності (7.7) зробити заміну , то ця рівність приймає вигляд

(7.8)

Рівності (7.7) та (7.8)називають другою чудовою границею. Ця границя часто використовується в різних галузях науки, економіки.

Приклад 7. Обчислити при постійному а.

Розв’язування.

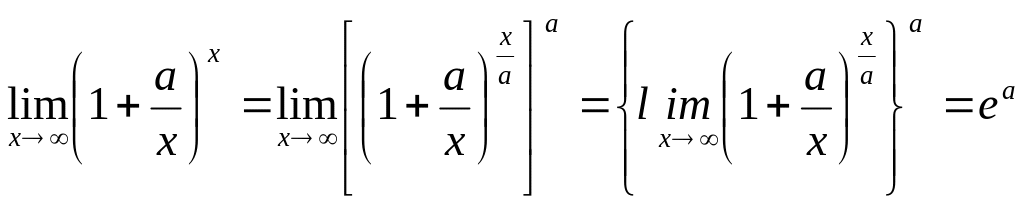
Приклад 8.

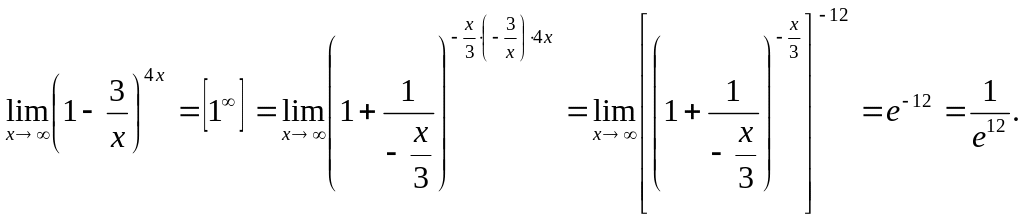
Приклад 9.

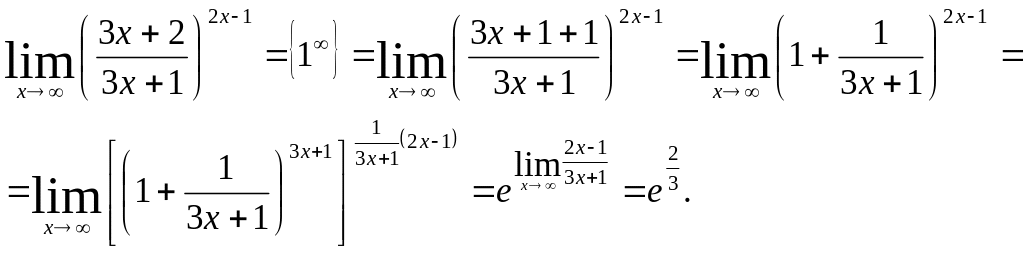
Застосування другої чудової границі у банківській справі. неперервне нарахування відсотків на капітал.

Приклад 10. 10 млн грош. од. інвестовані на 2 роки за ставкою 120 % річних. Треба знайти нарощувану за цей час суму і її приріст при нараху­ванні:

а) щорічно; б) по півріччям; в) щокварталу; г) щомісяця.

Розв'язання. Скористаємось формулою

1) при простих: ,

2) при складних

3) при складних відсоках з часткою нарахування m раз на рік

при

де n=2, P=10 млн грош. од., q=120%, r= m=1,2,4,12 відповідно для випадків а), б), в), г).

Позначимо — приріст суми . Результати зведемо до таблиці.

Випадок	т		млн грош.од.	, млн грош.од.
а)	1	=4,8400	48,400	38,400
б)	2	=6,5536	65,536	55,536
в)	4	=8,1573	81,573	71,573
г)	12	=9,8497	98,497	88,497

Приклад 11. При одній і тій же відсотковій ставці за схемою неперервного нарахування відсотків вкладник С через 2 роки одержує 1000 грош. од., вкладник D через 4 роки одержує 600 грош. од. Знайти відсоткову ставку q, якщо первісний вклад вкладника С вдвічі більше, ніж вклад вкладника D .

Розв'язання. Скористаємось формулою

.

Тоді

де - - початкові вклади вкладників С та D відповідно,

Враховуючи, що , маємо

1000 =1200 .

Звідси

;

2 ∙ r = ln 1,2 ; r = 0,5 ln l,2 = 0,09116 ,

q = r∙100 % ≈ 9,1 %.