
- •З дисципліни
- •I семестр
- •II семестр
- •Перший семестр Змістовний модуль №1 тема 1. Системи лінійних алгебраїчних рівнянь і методи їх розв’язання
- •3. Властивості визначників:
- •5. Теорема Крамера:
- •Множення матриць
- •Додавання матриць
- •Віднімання матриць
- •Добуток матриці на число
- •7. Обернена матриця
- •8. Матричний спосіб розв’язання систем (слар)
- •9. Ранг матриці
- •10. Теорема Кронекера – Капеллі.
- •11. Метод Джордано - Гаусса – універсальний метод
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Тема2. Елементи векторної алгебри. Вектори в просторі r3.
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Тема 3. N-вимірний лінійний простір. Перехід від одного базиса до іншого.
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Змістовний модуль 2. Тема 4. Аналітична геометрія на площині. Пряма лінія на площині.
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Тема 5. Криві другого порядку.
- •Тема 6. Деякі елементи аналітичної геометрії в просторі План
- •4.2. Канонічні рівняння прямої
- •4.3 Параметричні рівняння прямої
- •Контрольні питання
- •Завдання для самостійного виконання
- •Тема 7. Вступ в математичний аналіз. Поняття границі та методи її знаходження.
- •1 Означення функції.
- •4 Основні властивості границі змінної величини.
- •6 Техніка знаходження границь.
- •7 Перша чудова границя
- •Питання для самоперевірки
- •Завдання для самостійного розв’язання
- •Тема 8.Неперервність функції. Теореми про неперервні функції.
- •4 Властивості:
- •Питання для самоперевірки
- •Завдання для самостійного розв’язання
- •Тема 9. Поняття похідної. Похідні функцій, заданих явно, неявно, параметрично.
- •Задачі, які привели до поняття похідної
- •Означення похідної та її геометричний зміст
- •Зв’зок диференційованості функції з неперервністю
- •Основні правила диференційювання
- •6. Поняття диференціала функції та його застосування до наближених обчислень. Геометричний зміст диференціала
- •7. Похідні вищих порядків
- •2. Одержане алгебраїчне рівняння розв’язуємо відносно відомого :
- •9. Похідна степенево-показникової функції.
- •Похідна функції, заданої параметрично.
- •Питання для самоперевірки
- •Завдання для самостійного розв’язання
- •Контрольні завдання
- •Тема 10. Застосування похідних до дослідження функції.
- •Завдання для самостійного розв’язання.
- •Другий семестр Змістовний модуль 3
- •Тема 1. Невизначений інтеграл, основні методи інтегрування
- •Тема 2. Інтегрування дробово – раціональних функцій.
- •Тема 3: Інтегрування деяких класів функцій.
- •Тема 4. Диференціальні рівняння I- порядку. Задача Коші.
- •Означення 1.
- •Питання для самоперевірки
- •Завдання для самостійного виконання:
- •Змістовний модуль 4 Тема 5. Функція двох змінних
- •Тема 6. Екстремум функції двох змінних. Спосіб найменших квадратів.
- •Приклад 1.
- •Тема 7. Числові та степеневі ряди.
- •Питання для самоконтролю.
Тема 7. Вступ в математичний аналіз. Поняття границі та методи її знаходження.
Означення функції, область визначення функції, множина значень. Основні елементарні функції та їх графіки (у=ах, y=lnx, у=arctgx, y=arcctgx) .
Поняття границі числової послідовності.
Поняття границі функції. Односторонні границі, умова існування границі функції.
Поняття границі змінної величини. Основні властивості границі змінної величини.
Нескінченно малі і нескінченно великі змінні величини та їх властивості.
Техніка знаходження границь.
Перша чудова границя та її застосування для розкриття невизначеності
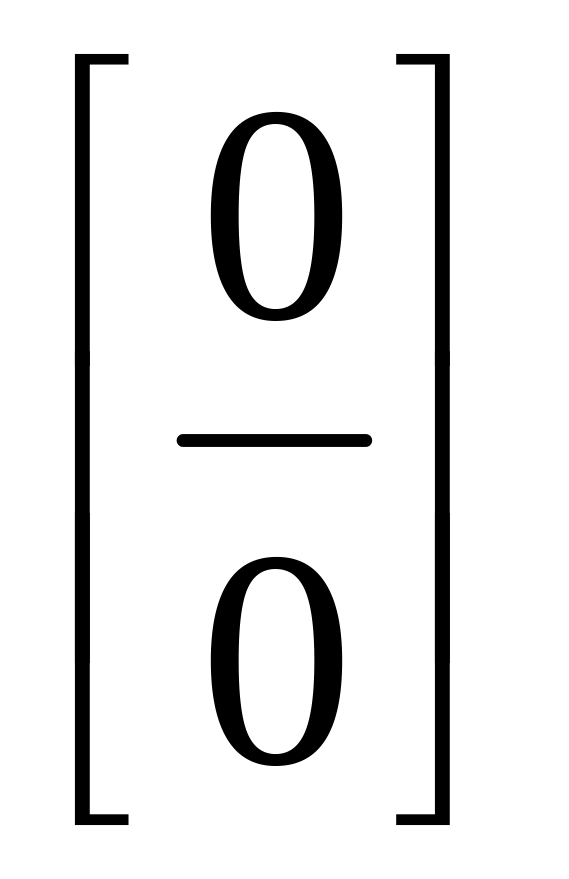 .
.Друга чудова границя (без доведення) та її застосування до розкриття невизначеності
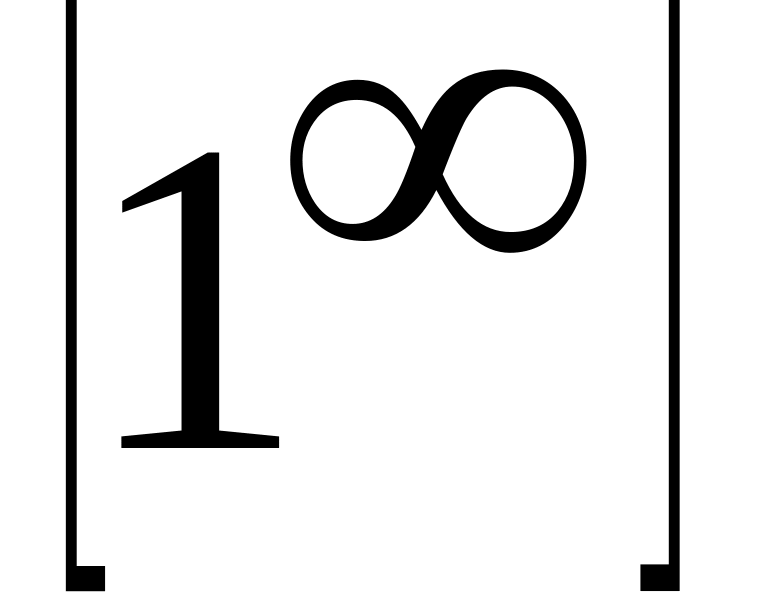 .
.Застосування другої чудової границі у банківській справі. Неперервне нарахування відсотків на капітал.
1 Означення функції.
Означення
1. Функцією
називають правило або закон f,
згідно
якого деякому значенню змінної величини
![]() ставиться у відповідність змінна
ставиться у відповідність змінна
![]() і записують
так y=f(x).
і записують
так y=f(x).
Область
визначення функції: сукупність
усіх числових значень, які може приймати
аргументи x
і при яких функція
![]() визначена.
визначена.
Функцію однієї змінної можна задати аналітично, таблично, графічно, мовно й за допомогою комп’ютерних програм.
Функцію у=f(x) називають однозначною, якщо кожному значенню х відповідає одне значення у. Функцію у називають багатозначною, якщо кожному значенню х відповідає кілька значень у.
При аналітичному значенні функція задається однією або кількома рівностями, що зв’язують залежні і незалежні змінні.
При табличному способі функціональна залежність задається у вигляді таблиці, в якій для кожного числа значення х вказано відповідне числове значення у.
Графічний спосіб найбільш наглядний і базується на застосуванні методу координат. Функціональну залежність зображають лінією.
Елементарні функції
Степенева у = хn
Показникові у = ах а > 0, а
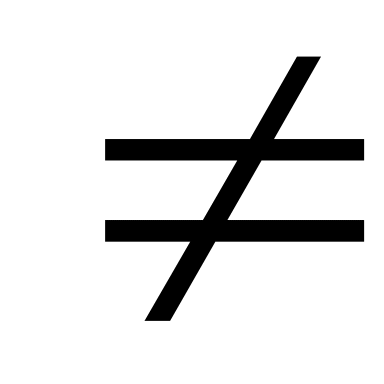 1
1Експоненціальна у = ех е = 2,7182
Логарифмічна у = logax а >0, а 1
Натуральний логарифм у = lnx
Тригонометричні y = cosx (sin, tg, ctg, sec, cosec)
Оберенено тригонометричні y = arcsinx, y=arctgx.
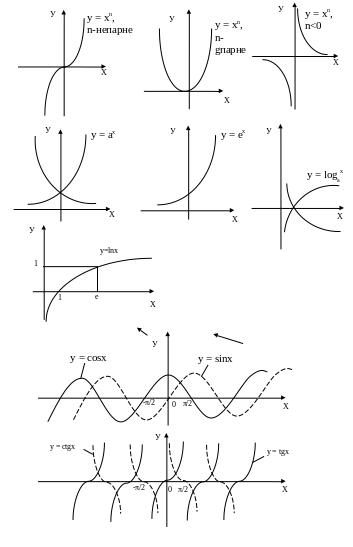
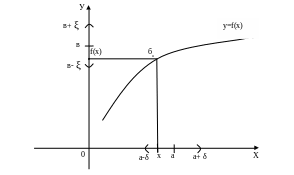
2![]() ξ
>0) знайдеться або наступить такий
момент в зміні її значень,
починаючи з якого виконується нерівність
ξ
>0) знайдеться або наступить такий
момент в зміні її значень,
починаючи з якого виконується нерівність
![]() ξ
ξ
- ξ < х – а < ξ
а – ξ < х < а + ξ
а- ξ а а+ ξ
Інтервал (а – ξ; а + ξ) = ξ а і називають епсілон окіл точки а . Tому можна коротко сказати означення границі: число а називають границею змінної величини х, якщо для будь-якого ξ окoлy (ξ а) точки а наступить такий момент її зміни, починаючи з якого всі її значення попадуть в цeй окіл. Запис. так : х → а.
Означення
3. Число а
називають границею
числової послідовності
![]() ,
якщо
ξ > 0
,
якщо
ξ > 0
![]() N
= N(ξ)
N
= N(ξ)
![]() ≥ N:
≥ N:
![]() ξ, тобто
ξ, тобто
![]() є ξa.
є ξa.
Записують
так:
![]() =а
або
=а
або
![]()
Приклад
1.
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
ξ
![]()
![]()
![]()
![]() <
<![]()
ξ
![]()
![]() <
<![]()
і т. д. ξ
Висновок: яке б мале число ξ ми не взяли, то завжди знайдеться номер N починаючи з якого в епсілон околі точки 2 буде нескінченна кількість членів послідовності, а поза ним – скінчена, тому точку 2 називають границею даної послідовності.
3![]() цей запис означає:
ξ >0
цей запис означає:
ξ >0
![]() (ξ)>0
із виконання нерівності
(ξ)>0
із виконання нерівності
![]() <
<![]() слідує виконання нерівності
слідує виконання нерівності
![]() <
ξ.
<
ξ.
Приклад
2.
![]()
![]()
ОДЗ:
х є
![]()
![]()

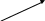
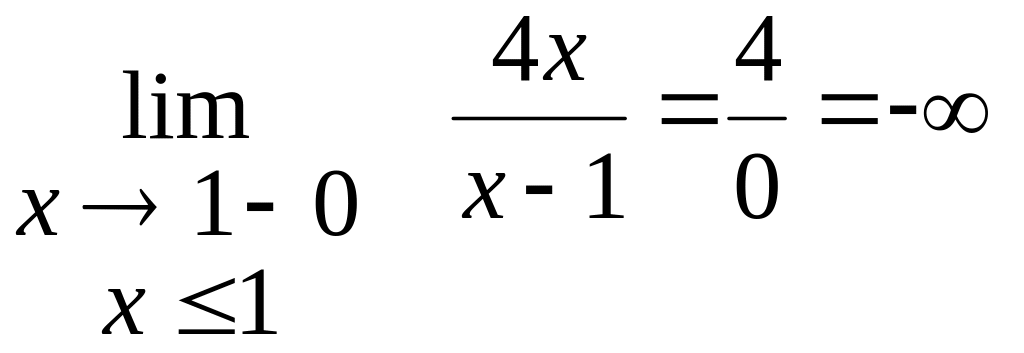 границя
зліва
границя
зліва
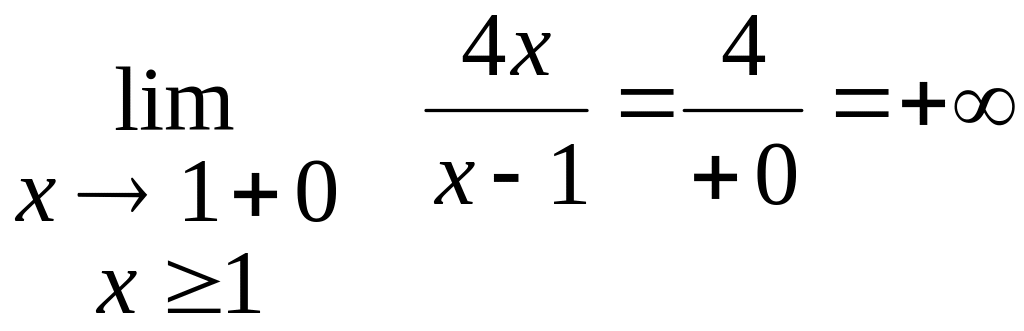 границя
справа
границя
справа
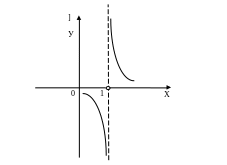
Тому границя не існує.
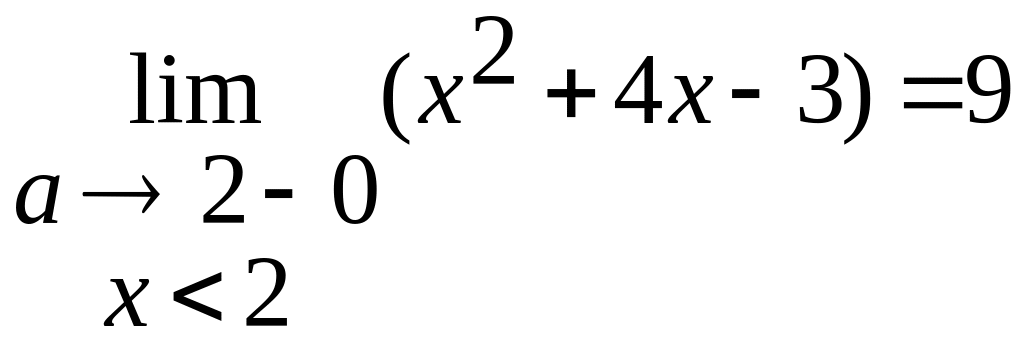
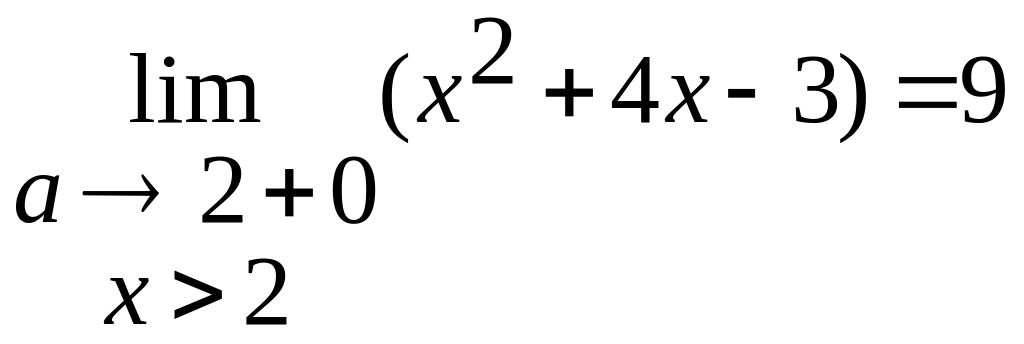
Односторонні
границі:
![]() - границі зліва,
- границі зліва,
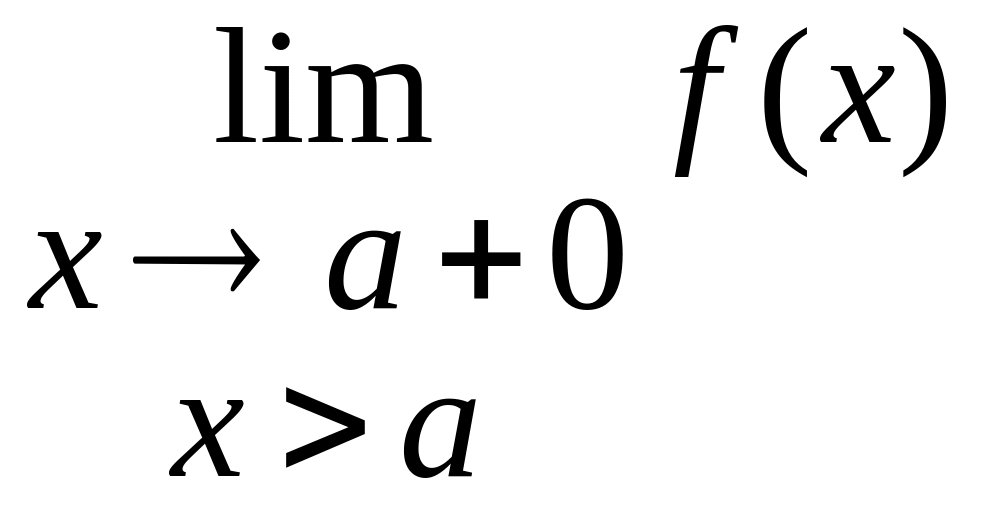 -
границя зліва.
-
границя зліва.
Умова
існування границі функції:
границя зліва дорівнює границі справа.
![]() .
(7.1)
.
(7.1)
