Тема 6. Деякі елементи аналітичної геометрії в просторі План

1. Поняття поверхні в просторі та її рівняння.

2. Поняття лінії в просторі та її рівняння.

3. Рівняння площини в просторі:

3.1 Рівняння площини, яка проходить через дану точку перпендикулярна даному вектору.

3.2 Загальне рівняння площини та його дослідження.

3.3 Рівняння площини, що проходить через три дані точки.

4. Рівняння прямої лінії в просторі:

4.1 Рівняння прямої через дві дані точки.

4.2 Канонічне рівняння прямої.

4.3 Параметричні рівняння прямої.

1. Поверхня – це геометричне місце точок, координати яких задовольняють рівняння

F (x; y;z) = 0 (6.1)

2. Лінією l в просторі можна розглядати як лінію перетину двох поверхонь або геометричне місце точок, що знаходяться одночасно на обох поверхнях, F₁(x;y;z)=0 і F₂(x;y;z) = 0 рівняння двох поверхонь, які визначають лінію l, то координати точок цієї лінії задовольняють систему двох рівнянь з трьома невідомими:

(6.2)

Рівняння системи сумісно визначають лінію l і називають рівнянням лінії в просторі.

Лінію в просторі можна розглядати як траєкторію рухомої точки. При такому підході лінію в просторі задають векторним параметральним рівнянням:

Векторне параметральне відповідає скалярному параметральному рівняння

х = х(t); y = y(t); z = z(t) – проекції вектора на осі координат.

3.1. Рівняння площини, що проходить через задану т. М₀(х₀;у₀;z₀) перпендикулярно заданому вектору = (А, В, С)

В ізьмемо довільну точку площини М(х; у; z) і побудуємо вектор

= (x – x₀; y – y₀; z – z₀)

Вектори та перпендикулярні, тому їх скалярний добуток дорівнює нулю. Отже, маємо:

A (x – x₀) + B (y – y₀) + C (z – z₀) = 0 (6.3)

Приклад№1

Задана площина Р: -2x+y-z-1=0 і точка M(1,1,1). Написати рівняння площини Р', що проходить через точку М паралельно площині Р.

Розв’язання: Скористаємося рівнянням площини, що проходить через точку, перпендикулярно до нормального вектора. Через те, що Р'║Р, їх нормальні вектори рівні:

-2(x-1)+(y-1)-(z-1)=0; Р': -2x+y-z+2=0

3.2. Теорема. Будь-яке рівняння першого степеня відносно x,y,z визначає площину.

Доведення. Розглянемо довільне рівняння першого степеня відносно x,y,z:

Ах + Ву + Сz + D = 0 (6.4)

Це рівняння має нескінченну кількість розв’язків. Нехай (х₀;у₀;z₀) один з цих розв’язків. Тоді маємо:

Ах₀ + Ву₀ + Сz₀ + D = 0 (6.5)

Різниця рівнянь (7.4) та (7.5) має вигляд:

A (x – x₀) + B (y – y₀) + C (z – z₀) = 0

Ліву частину цієї рівності можна розглядати як скалярний добуток векторів =(А, В, С) та = (x – x₀; y – y₀; z – z₀).

З рівності нулю скалярного добутку випливає, що перпендикулярний .Отже, кінці вектора лежать в площині, перпендикулярній і яка проходить через точку М₀ тобто рівняння (6.3), а значить і (6.4), визначає площину перпендикулярну вектору .

Означення. Рівняння вигляду (6.4) називають загальним рівнянням площини в просторі.

3.3. Рівняння площини, що проходить через три точки М₁(х₁;у₁;z₁), М₂(х₂;у₂;z₂), М₃(х₃;у₃;z₃) знаходять за формулою:

(6.6)

Приклад 2.

Знайти рівняння площини Р, що проходить через точки А(2,-1,1), В(5,5,4) і С (3,2,-1).

Розв’язання: Знаходимо за формулою (6.6)

Р: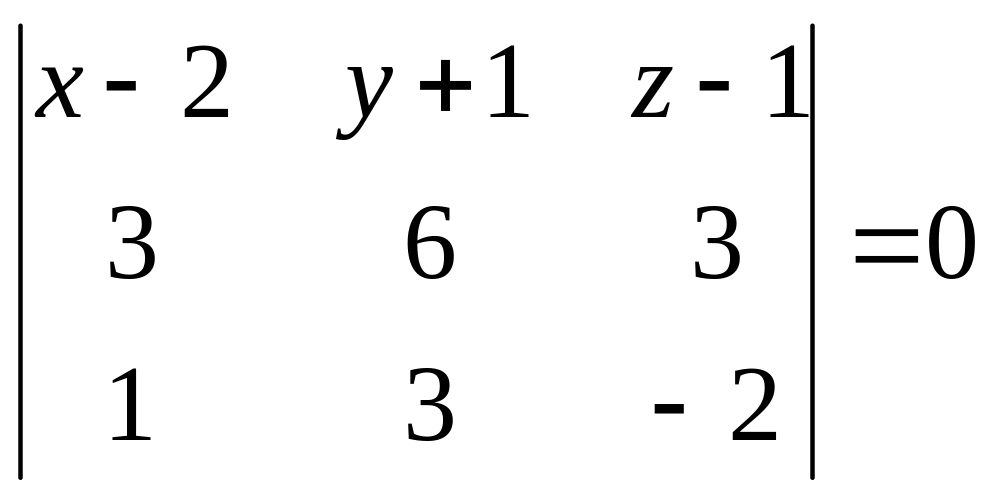

-21(x-2) +9(y+1) +3(z-1) =0,

-7(x-2) +3(y+1) +(z-1) =0,

Р: -7x+3y+z+16 =0

4.1. Рівняння прямої, що проходить через дві точки

Нехай на прямій задані дві точки М₁(х₁;у₁;z₁), М₂(х₂;у₂;z₂)

знайдемо рівняння такої прямої нехай напрямним вектором прямої буде вектор = = (x₂ – x₁; y₂ – y₁; z₂ – z₁). Тоді, підставляючи координати вектора в рівняння (7.8), одержимо рівняння

, (6.7)

яке називають рівняння прямої, що проходить через дві задані точки.

Приклад №3

Скласти рівняння прямої що проходить через точки М (1,2) та К(3,5)

Розв’язання: Використаємо рівняння прямої, що проходить через дві точки

Маємо 3x-2y+1=0.