Питання для самоперевірки.

1. Означення лінії на площині.

2. Рівняння прямої, яка проходить через дану точку в заданному напрямку.

3. Який вигляд має рівняння прямої з кутовим коефіцієнтом?

4. Запишіть загальне рівняння прямої і проведіть його дослідження.

5. Рівяння прямої через дві дані точки.

6. Як знайти кут між прямими?

7. Розкажіть про знаходження точки перетину двох прямих.

8. Сформулюйте умови паралельності і перпендикулярності прямих.

Задачі для самостійного розв’язання.

1. Знайти точки перетину прямої 2х – 3у – 12 = 0 з координатними осями і побудувати цю пряму.

2. Сторони АВ, ВС і АС трикутника задані відповідно рівняннями: 4х + 3у – 5 = 0, х – 3у + 10 = 0, х – 2 = 0. Знайти координати його вершини.

3. Дано пряму 2х + 3у + 4 = 0. скласти рівняння прямої, яка проходить через точку М0 (2; 1): 1) паралельно до заданої прямої; 2) перпендикулярно до заданої прямої.

4. Дано рівняння двох сторін прямокутника х – 2у = 0, х – 2у + 15 = 0 і рівняння однієї з його діагоналей 7х + у -15 = 0. Знайти вершини прямокутника.

5. Знайти кут φ між двома прямими:

   1. 5х – у + 7 = 0, 3х + 2у = 0; 2) 3х- 2у + 7 = 0, 2х + 3у – 3 = 0.

6. Дано дві протилежні вершини квадрата А (-1; 3) і С (6; 2). Скласти рівняння його сторін.

7. При якому значенні а три прямі 2х – у + 3 = 0, х + у + 3 = 0 , ах + у – 13 = 0 перетинаються в одній точці?

8. Знайти рівняння прямої, яка відображає зміну врожайності 1 га орної землі протягом 17 років, якщо в перший рік з 1 га було зібрано 21 ц. зернових, а в останній – 37 ц.

9. Витрати виробництва на 20 одиниць товару складають 2000 грн., на 60 одиниць товару – 3000 грн. Знайти витрати виробництва на 30 одиниць товару за умови, що витрати залежать від обсягу продукції лінійно.

Тема 5. Криві другого порядку.

План

1. Еліпс. Канонічне рівняння еліпса. Властивості. Графік.

2. Гіпербола. Канонічне рівняння. Властивості. Графік. Асимптоти.

3. Парабола. Канонічне рівняння . Властивості. Графік.

4. Загальне рівняння кривої другого порядку та його спрощення за допомогою перетворень паралельного перенесення системи координат.

1. Означення: Еліпсом називають геометричне місце точок, сума відстаней яких до двох фіксованих точок площини є величина стала (2а). Фіксовані точки називаються фокусами еліпса.

Складемо канонічне рівняння еліпса.

Знайдемо рівняння еліпса. Позначимо через та фокуси еліпса. Вісь абсцис проведемо через фокуси та , а вісь проведемо через середину відрізка [ ] перпендикулярно до осі .

Позначимо відстань між фокусами 2с.У такій системі координат .Візьмемо довільну точку М(х, у) еліпса. За означенням еліпса маємо:

│ │+│ │=2а

Але │ │= ; │ │=

Тому одержуємо рівняння еліпса вигляду:

+ =2а

Будемо спрощувати це рівняння . Перенесемо один корінь у праву частину рівняння та піднесемо до квадрату обидві частини:

→

Знову піднесемо до квадрату обидві частини, тоді одержимо:

ax² - 2a²cx + a²c² + a²y² = c²x² - 2a²cx + a⁴→ (a²-c²)x² +a²y² = a² (a²-c²)

Поділимо обидві частини останньої рівності на a²(a²-c²) і одержимо:

Згідно нерівності а²>c² можна позначити

b²= a²-c² (5.1)

Тоді рівняння еліпса прийме вигляд

(5.2)

Рівняння (7.2) називають канонічним рівнянням еліпса.

Дослідження рівняння еліпса дозволяє зробити висновок, що параметри рівняння а та b дорівнюють півосям еліпса , розташовані на осях координат О_х і О_у , відповідно. Еліпс має форму зображену на малюнку.

Зауваження: Якщо b > а, то фокуси еліпса лежать на осі Оу.

Властивості еліпса

1. Рівняння (5.2) містить змінні х та у лише в парних степенях, якщо т.(х;у); (-х;-у). Тому еліпс симетричний відносно осей Ох і Оу, а також відносно т.О (0;0), яку називають центром еліпса. Отже, для встановлення форми еліпса достатньо дослідити ту його частину, яка розміщується в одному координатному куті.

2. В першому координатному куті х ≥ 0, у ≥ 0, тому з рівності (5.2) маємо . Звідси випливає, що т.А(а;0) та В(0;b) належать еліпсу, при чому якщо х збільшується від 0 до а, то у зменшується від b до 0. Крім того не існує точок еліпса, у яких x > a, бо зараз (5.2) при х > 0 не має змісту. Еліпс перетинає осі координат в т.А₁(а;0), А₂(-а;0), В₁(0;b), В₂(0;-b). Ці точки називаються вершинами еліпса.

Таким чином з властивостей 1і 2 випливає, що будь-який еліпс має 2 взаємо перпендикулярні осі симетрії (головні осі еліпса) та центр симетрії (центр еліпса). Увесь еліпс вміщується в прямокутник із сторонами 2а і 4b. Сторони прямокутника дотикаються до еліпса в його вершинах х.

3. Якщо а = b, то рівняння (5.2) набирає вигляду: х² + у² = а², тобто дістанемо рівняння кола. З формули (5.2) випливає, що при а = b значення с = 0, тобто коло – це еліпс, у якого фокуси збігаються з його центром.

Міра відхилення еліпса від кола характерна величиною ε, яка називається ексцентриситетом еліпса і дорівнює відношенню половини його фокальної відстані до довжини більшої півосі.

, при чому а ≤ ε ≤ 0, оскільки 0 ≤ с < а, з формули а² – с² = b, - дістанемо:

Отже, якщо ε = 0, то b = a, тобто еліпс перетворюється в коло, якщо ε наближається до 1, то відношення осей зменшується, тобто еліпс все більше розтягується вздовж осі Ох.

4. М(x;y) – доводиться т. еліпса з фокусами F₁ і F₂. Відстані F₁M = і F₂M =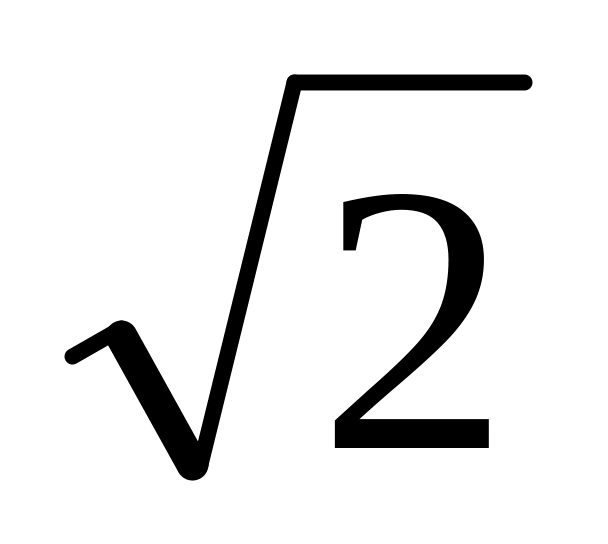 називаються фокальними радіусами. Очевидно + = 2а.

Прямі називаються директрисами еліпса.

Відношення фокальних радіусів довжина точок еліпса до відстаней цієї точки від відповідних директрис є величина стала і дорівнює ексцентриситету еліпса, тобто

2. Означення: Гіперболою називають геометричне місце точок, різниця відстаней яких до двох фіксованих точок площини є величина стала (2а). Фіксовані точки називаються фокусами гіперболи.

Виведення рівняння гіперболи здійснюється аналогічно до виведення рівняння еліпса. Таким же чином позначаються фокуси та довільна точка М гіперболи. За означенням гіперболи маємо:

║ М│-│ М║=2а → │ М│-│ М│=±2а

Перехід в останній рівності до координатної форми та алгебраїчні перетворення дозволяють одержати рівняння гіперболи вигляду:

Для гіперболи ,тому і рівняння гіперболи буде мати вигляд:

(5.3)

Рівняння (7.3) називають канонічним рівнянням гіперболи.

Зауваження: Рівняння є канонічним рівнянням гіперболи, вершини якої лежать на осі Оу.

Прямокутник із сторонами 2а і 2b називається основним прямокутником гіперболи.

При побудові гіперболи доцільно спочатку побудувати основний прямокутник C₁D₁CD, провести прямі, що проходять через протилежні вершини цього прямокутника, асимптоти гіперболи і визначити вершини А₁ і А₂ гіперболи.

Рівняння також визначає гіперболу, яка називається спряженою до гіперболи . Ця гіпербола показана на рисунку штрих-лінією. Її вершини

лежать в точках В₁(0;b) i B(0;-b), а її асимптоти збігаються з асимптотами гіперболи .

Рівняння асимптот мають вигляд:

(5.4)

- асимптоти гіперболи

3 . Означення: Параболою називають геометричне місце точок, рівновіддалених від фіксованих точок площини і даної прямої. Фіксовані точки називаються фокусами, дану пряму – директрисою.

Для одержання рівняння параболи у системі координат хОу вісь Ох побудуємо перпендикулярно до директриси і так , щоб вона проходила через фокус параболи — точку F. Початок координат візьмемо посередині між фокусом та директрисою.

Відстань між фокусом F та директрисою позначимо р. Тоді F( , рівнянням бісектриси буде x= - . Візьмемо довільну точку М(х, у) параболи.

Згідно з означенням параболи маємо:

│FM│=│KM│

У координатній формі ця рівність має вигляд:

Ця рівність є рівнянням параболи . Піднесемо до квадрату обидві частини і , спростивши одержаний вираз , одержимо рівняння вигляду:

y²=2px (5.5)

яке називають канонічним рівнянням параболи.

Зауваження. Парабола y²=-2px розташована зліва від осі Оу, симетрична з параболою y²=2px.

Рівняння x²=2qy визначає параболу ,віссю симетрії якої буде вісь Оу, а рівняння директриси має вигляд : y= -

4. Загальне рівняння кривої другого порядку має вигляд:

Ах² + Вху + Су² + Dх + Ey + F = 0 (5.6) , де А,В,С,D,E,F-довільні, дійсні числа .

В залежності від співвідношень між коефіцієнтами А, В, С будуть різні криві другого порядку та їх виродження . Наприклад:

(х² + у²)= 0; (х – у) (х + у) = 0

Рівняння (5.6) спрощується за допомогою формул паралельного перенесення системи координат, які мають вигляд:

M(x,y) O^/(x₀,y₀) M(x^/,y^/)

Приклад І. Спростити рівняння кривої і побудувати її

3х² + 4у² – 6х + 12у – 3 = 0

1) Виділяємо повний квадрат окремо по х і у. а² 2аb + b² = (a + b)²

3x² – 6x - 4y² + 12y – 3 = 0

3 (x² – 2x) - 4 (y² - 3y) – 3 = 0

3 (x² – 2x∙1 + 1² – 1²) - 4 - 3 = 0

3 (x – 1)² – 1) -4 (y - )² - ) – 3 = 0

3 (x – 1)² – 3 - 4 (y - )² + 9 – 3 = 0

3 (x – 1)² - 4 (y - )² = -6

- гіпербола

О′ (1; ) а =

b =

Приклад 2. Визначити лінію ,рівняння якої

2x²-8x+y²+6y+1=0 , та побудувати її.

Розв’язування. Спочатку об’єднаємо члени рівняння ,які містять х та у окремо ,тоді одержимо:

(2x²-8x)+(y²+6y)+1=0

Рівняння не зміниться ,якщо ми у першу дужку додамо та віднімемо 8,а в другій дужці 9. Тоді матимемо:

(2x²-8x+8-8)+(y²+6y+9-9)+1=0

Виділимо повні квадрати :

2(x-2)²+(y+3)²-8-9+1=0 2(x-2)²+(y+3)²=16

Позначимо

Звідси:

Якщо ми побудуємо нову систему координат x’o’y’,початок якої в точці о’(2,-3) , а осі o’x’та o’y’ паралельні осям старої системи ох та оу ,тоді у новій системі x’o’y’ координат рівняння має вигляд:

Це є канонічне рівняння еліпса з півосями a=2 ,b=4.

Отже задане рівняння є рівнянням еліпса ,який можна зобразити у системі координат.

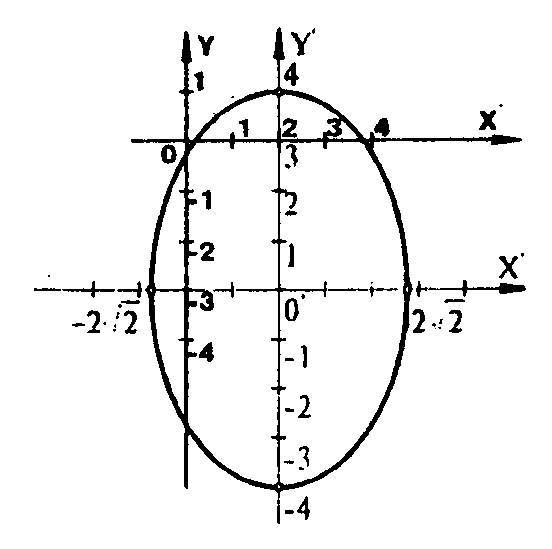
Питання для самоперевірки.

1.Що називається еліпсом ?

2.Записати канонічне рівняння еліпса .

3.Сформулювати означення гіперболи .

4.Записати канонічне рівняння гіперболи .

5. Дати означення асимптот для гіперболи .

6.Що називається параболою ?

7.Канонічне рівняння параболи .

8.Дати означення перетворень паралельного перенесення системи координат

Завдання для самостійного розв’язання .

1.Побудувати еліпс 9х²+25у²=225.Знайти :

а)півосі б)координати фокусів в)ексцентриситет г)рівняння директрис.

2.Написати канонічне рівняння еліпса, якщо :

а)a=3, b=2 б)а=5, с=4 в)с=3,ε=3/5 і відстань між директрисами дорівнює 32.

3.Написати рівняння еліпса з півосями а та b і центром у точці С(х₀ ,у₀) ,якщо відомо , що його осі паралельні координатним осям .

4. Написати рівняння гіперболи з півосями а та b і центром у точці С(х₀ ,у₀) якщо що її дійсна та уявна осі паралельні осям О_х і О_у відповідно.

5.Встановити , що кожне з наступних рівнянь визначає гіперболу, знайти її центр С, півосі рівняння асимптот та директрис:

а)16х²-9у²-64х-54у-161=0

б)9х²-16у²+90х+32у-367=0

в) 16х²-9у²-64х-18у+199=0

6.Побудувати наступні параболи , та знайти їх параметри:

а)у²=6х б)х²=5у

в) у²= -4х г) х²= - у

7.Написати рівняння параболи з вершиною у початку координат , якщо відомо, що парабола розташована симетрично відносно осі О_у та проходить через точку М(4,-8).