Вопрос 33

Объединение отношений. Объединять отношения можно только в том случае, когда заголовки объединяемых отношений совпадают. Результатом объединения является отношение, имеющее такой же заголовок, что и исход­ные отношения, а тело отношений включает в себя все кортежи, входящие хотя бы один раз в одно из исходных отношений.

ПримерЗ.1. Объединить отношения, представленные в табл. 3.3 и 3,4.

Результирующее отношение получается путём внесения в неё всех кор­тежей, входящих в исходные отношения с последующим исключением кор­тежей-дубликатов (Иванов Й.И. и Козлов К.К. получили по две двойки, но в результирующем отношении их фамилии встречаются только один раз).

Результат объединения отношений представлен в табл. 3.5.

Пересечение отношений. Эта операция также может быть выполнена только в том случае, если заголовки исходных отношений полностью совпа­дают. Результирующее отношение имеет тот же заголовок, а в тело отноше­ния включаются только кортежи, содержащиеся во всех исходных отноше­ниях.

Пример 3.2. Найти пересечение отношений табл.3.3 и 3.4.

Таблица 3.6 Список студентов, получивших неудовлетворительные оценки по обеим дисциплинам

Взятие разности отношений. В данном случае исходные отношения должны иметь совпадающие заголовки, результирующее отношение также будет иметь тот же заголовок. В тело отношения включаются только корте­жи, имеющиеся в уменьшаемом отношении и отсутствующие в вычитаемом отношении. При взятии разности А-В в результирующее отношение будут включены кортежи отношения А, не входящие в отношение В. Разность от­ношений В-А включает кортежи отношения В, не содержащиеся в отноше­нии А.

Пример 3.3. Составим списки студентов, получивших неудовлетвори­тельные оценки только по математике и только по физике.

Таблица 3.7 Список студентов, получивших неудовлетворительные оценки только по математике

Таблица 3.8 Список студентов, получивших неудовлетворительные оценки только по физике

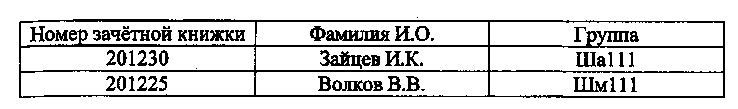
Прямое (декартово) произведение двух отношений. Эта операция возможна только в том случае, если заголовки отношений не содержат оди­наковых атрибутов. В случае совпадения наименований атрибутов необхо­димо их переименовать. Заголовок нового отношения включает в себя атри­буты обоих отношений, а тело отношения получается путём сцепления (кон­катенации) кортежей исходных отношений. Кардинальное число результи­рующего отношения равно произведению кардинальных чисел исходных от­ношений.

Пример 3.5. Пусть Принято решение: студенты, получившие две дойки, могут повторно сдать экзамены за дополнительную плату.

Найдём прямое произведение отношения табл. 3.6 и табл.3.9. Результат представлен в табл. 3.10.

Таблица 3.9 Список экзаменаторов

Каждый из исходных отношений имеет атрибут "Фамилия И.О." Вы­полнение операции прямого произведения возможно только после переиме­нования атрибутов.

Таблица 3.10 Ведомость платных переэкзаменовок

Вопрос 34

Ограничение отношения по некоторому условию. Исходными дан­ными этой операции являются отношение и условие по какому-нибудь атрибуту (знаки =, <, >, <, > и др.). Результатом выполнения операции ограниче­ния является отношение, заголовок которого совпадает с заголовком исход­ного отношения, а тело отношения содержит только кортежи, для которых выполнено условие.

Пример 3.6. В табл.3.11 приведено расстояние до места жительства ро­дителей студентов. Ставится задача составления списка студентов, чьи роди­тели живут на расстоянии более 100 км (S>100).

Таблица 3.11 Расстояние до места жительства родителей студентов

Результат выполнения операции ограничения приведён в табл. 3.12.

Таблица 1.12 Список студентов, родители которых живут далее 100 км

Одновременно на отношение может накладываться несколько ограни­чений, определённых часто для разных атрибутов.

Например, составим список студентов группы ШаШ, чьи родители живут далее 100 км. Этот список можно составить путём поочерёдного вы­полнения операций ограничений (сначала составим список всех студентов, родители которых живут далеко, затем на полученное отношение наложим второе ограничение - выберем студентов, обучающихся в группе Ша111).

При этом, как правило, составляют одно сложное ограничение путём соединения простых ограничений с помощью связок AND, OR, NOT и ско­бок. В рассматриваемом случае условие будет выглядеть так: (S>100 AND Группа =Ша111).

Операция взятия проекции. Проекцией отношения А по атрибутам X Z...Z (эти атрибуты принадлежат отношению А) называется отношение с за­головком X,Y, ...Z и телом, содержащем кортежи атрибутов X,Y, ...Z, при этом кортежи не должны повторяться. Таким образом, проекция отношения по­зволяет выделить столбцы таблицы.

Пример 1.7. Взять проекции отношения табл. 1.13 по атрибутам "Место практики", "Должность", "Место практики, должность".

Таблица 1.13 Список студентов, прошедших практику

Таблица 1.14 Проекции отношений

Операция соединения отношений. Общая операция соединения от­ношений предусматривает наличие двух отношений и простого условия. В этом случае получается отношение, представляющее собой прямое произве­дение исходных отношений, но в тело отношения включаются только корте­жи, удовлетворяющие условию.

Наиболее часто используется естественное соединение [1]. Пусть за­даны два отношения с заголовками Л$0, ...Х& Yj,...Y^ и B(Y_},...Y_N, Z],...Zm), при этом именования атрибутов Y_h...Y_N обоих отношений совпадают. В ре­зультате операции соединения отношений получится отношение, заголовок которого будет включать в себя все атрибуты С(Х_Ь ...Хк, Y_]t...Y_N, Z;,...Za^, a тело отношения предусматривает сцепку тех кортежей отношений А и В, значения атрибутов Y_h... Y_N которых совпадают.

Если два отношения не имеют общих атрибутов, их соединение будет представлять собой прямое произведение.

Пример 3.8. Даны два отношения - успеваемость студентов на первом и втором курсах. При этом с первого курса был отчислен один студент и на второй курс принят другой студент. Предлагается создать сводную ведо­мость успеваемости (в сводную ведомость ни отчисленный, ни вновь приня­тый студенты не будут включены).

Операция деления отношений. Пусть отношение А имеет заголовок (Xj, ...Xx, Yj, ...Г#), а отношение В - (X_h ...Xg), частным от деления А/В явля­ется отношение С с заголовком (Г/,... Уц), в тело которого включены только кортежи отношения А, атрибуты (X_Jt ...Xg) которых совпадают с аналогич­ными атрибутами отношения В.

Пример 1.9. Делимое отношение представляет собой ведомость успе­ваемости студентов, а делитель -условие получения повышенной стипендии. В результате деления полученное отношение будет содержать список сту­дентов, получающих повышенную стипендию.